前提：“不行，你这图不能这么存，要用struct”，“ddy，你是恶魔吧，我就用数组存”——真香！
正文
首先，分析题意，原本的标准路径是树，他问选那两条新加的边会让原本的图存在环。
我们可以先画出一颗小树来看这个性质：
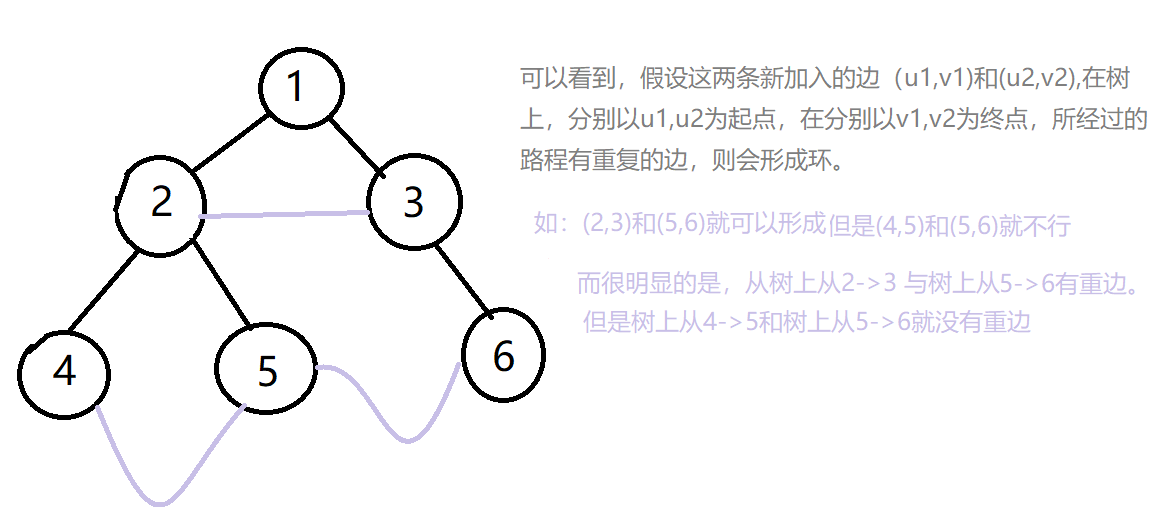
所以就变为了求树上有多少边之间有重复的边。这时，谈到树上的路径，应该很容易想到LCA，因为要想从一个点u走到v，一定要这么走：u->LCA->v
而此时，我们在树上讨论这些，对于我这个蒟蒻来说太难了，所以考虑把从u到v的路从LCA开始拆成两份：u->LCA,v->LCA;
而此时，问题则变为了：给你n条链，求他们重复的数量。而由于成环的性质，我们可以知道：当我们真的把这些都拆开后，会有一些重边。
对于重边，我们可以画图来更深刻地了解怎么处理这些重边
在了解平面上重边处理时，首先我们应该知道，出现重边，当且仅当u和v到LCA的路程上有重复时才会出现，如图：
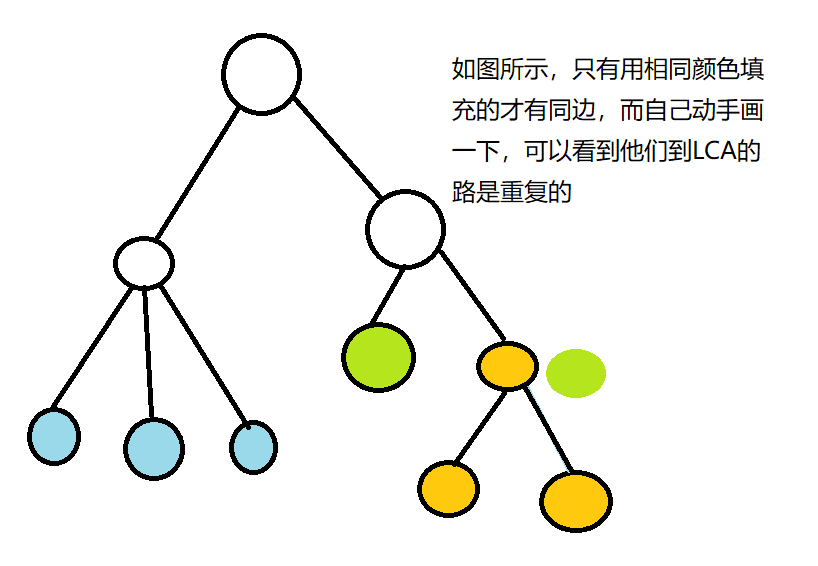
然后，让我们去考虑怎么求平面上链之间的重复
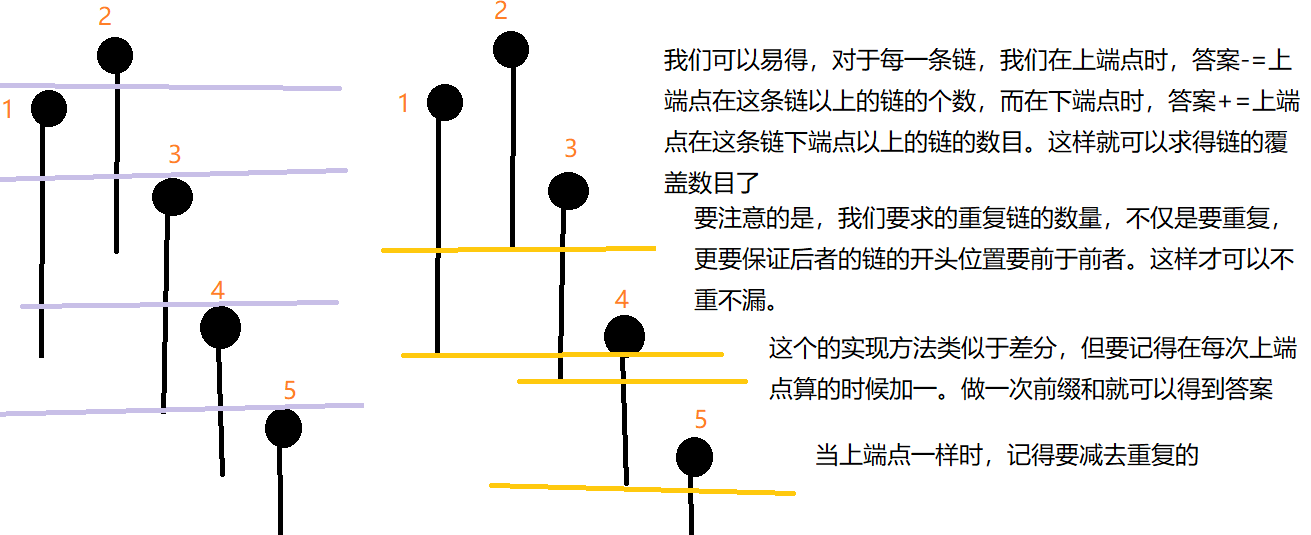
所以进行类比推理，我们就可以知道，在树上做前缀和可以得到的效果是一样的。
然后说明如何处理重复边的预先处理：
我们可以将每次读入的，要新加的边的两个点，在已经建好的树上找两个点最接近LCA（anc[i])但不是LCA的点UU，VV
为什么要跳到UU/VV？原因如下：
1.这样可以尽量减少误差：要是都跑到LCA，则会造成原本两个LCA一样，但到LCA的路程不一样，没有重边的两个点被判为一致的
2.这样有利于累计重复边的次数：我们可以考虑把“边权”放置到点上：这里的“边权”是指你重复过条边的次数，每个点所记录的值是在指这个点上面那条边的次数
而此时，在平面中上端点一样的情况，在树上就是两个点都可以跳到UU/VV
这时，还应注意一点，就是树上两点之间距离的计算，这很简单，所以我就放个图就好了
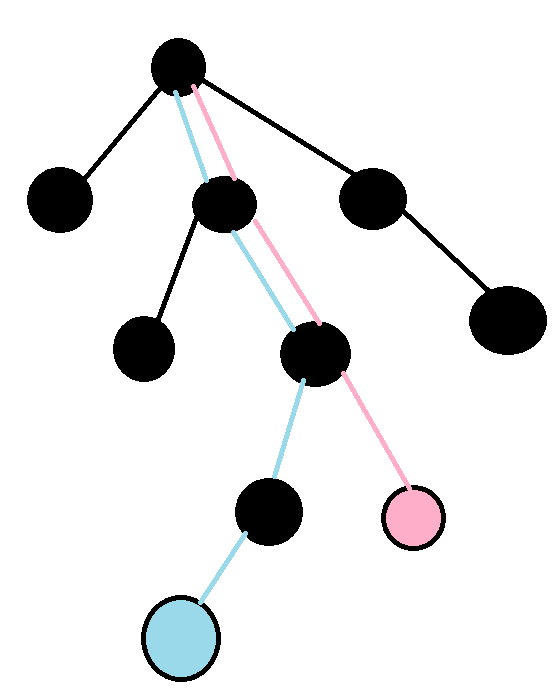什么，你问为什么我要画这么复杂，，对不起，千金难买我乐意
愉悦的代码时间
1 #include<iostream> 2 #include<cstdio> 3 #include<map> 4 using namespace std; 5 #define ll long long 6 inline int read(){ 7 int f=1,x=0;char ch=getchar(); 8 while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} 9 while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} 10 return x*f; 11 } 12 const int MAXN=2e5+5; 13 int n,m,head[MAXN];ll ans; 14 int fa[MAXN][21],dep[MAXN],tot,x,y; 15 int T[MAXN],num[MAXN],anc[MAXN],u,v; 16 pair<int,int> node[MAXN]; 17 map< pair< int,int >,int > Tpi; 18 struct EDGE{int next,to;}edge[MAXN<<1]; 19 /* 20 head[MAXN]和edge[MAXN<<1]是用来存图的 21 fa[MAXN][21]是用来找LCA的（2^20>=MAXN,所以 第二维是21） 22 fa[i][j]意思是从i开始，向上走2^j步后达到的节点 23 dep[MAXN]代表树上每个节点的深度 24 T[MAXN]相当于一个桶，记录这个点出现了几次 25 anc[MAXN]用来放LCA num[MAXN]用来放点权 26 node[MAXN]用来放新的边 27 map用来看这两个点同时向上走的时候，两条链开头相同的次数 28 */ 29 inline void addEdge(int u,int v) { 30 edge[++tot].next=head[u];edge[tot].to=v;head[u]=tot; 31 }//存图，强烈建议用struct存图，我用数组存已经翻车了（很大可能是因为我菜） 32 void dfs1(int u){ 33 for(register int i=1;i<=20;++i) 34 fa[u][i]=fa[fa[u][i-1]][i-1]; 35 dep[u]=dep[fa[u][0]]+1; 36 for(register int i=head[u];i;i=edge[i].next){ 37 int v=edge[i].to; 38 if(v==fa[u][0]) continue; 39 fa[v][0]=u; dfs1(v); 40 } 41 } 42 inline int lca(int u,int v){ 43 //十分正常的求LCA的程序 44 if(dep[u]<dep[v]) swap(u,v); 45 for(register int i=20;i>=0;--i) 46 if(dep[fa[u][i]]>=dep[v]) u=fa[u][i]; 47 if(u==v) return u; 48 for(register int i=20;i>=0;--i) 49 if(fa[u][i]!=fa[v][i]) 50 u=fa[u][i],v=fa[v][i]; 51 return fa[u][0]; 52 } 53 inline int gettop(int bot,int top){ 54 //找到两个点LCA下面的那一个点 55 if(top==bot) return -1926; 56 //如果bot就是他俩的LCA的话，就不存在那种最接近LCA 57 //但不是LCA和本身的点，返回-1926 58 for(register int i=20;i>=0;--i) 59 if(dep[fa[bot][i]]>dep[top]) bot=fa[bot][i]; 60 return bot; 61 } 62 void dfs2(int u,int curNum){ 63 //在树上求前缀和 64 num[u]=curNum; 65 //把边权下放到点权后，u这点就是上面的边的出现次数 66 for(register int i=head[u];i;i=edge[i].next){ 67 //向下遍历这棵子树 68 int v=edge[i].to; 69 //因为DFS2()要求的是这棵树的前缀和，又根据点权的定义 70 //所以要找到要求的点的上面一份 71 if(v!=fa[u][0]) dfs2(v,curNum+T[v]); 72 //如果没有找到u的父亲，就向下继续找，点权继续下放 73 } 74 } 75 int main(){ 76 n=read();m=read(); 77 for(register int i=1;i<=n-1;++i){ 78 u=read();v=read(); 79 addEdge(u,v);addEdge(v,u); 80 }dfs1(1); 81 for(register int i=1;i<=(m-(n-1));++i){ 82 u=node[i].first=read();v=node[i].second=read(); 83 anc[i]=lca(u,v); 84 int uu=gettop(u,anc[i]); 85 int vv=gettop(v,anc[i]); 86 if(uu!=-1926) ans-=T[uu]+1,T[uu]++; 87 if(vv!=-1926) ans-=T[vv]+1,T[vv]++; 88 //如果可以找到任意一点离LCA最近的那一个点，如图所示 89 //则需要减去重复的路的个数并加1（不可以重复但也不可以减完）。 90 //且这个点经过次数++ 91 if(uu!=-1926&&vv!=-1926){ 92 if(uu>vv) swap(uu,vv); 93 ans-=Tpi[make_pair(uu,vv)]; 94 Tpi[make_pair(uu,vv)]++; 95 //此时代表两段拆分后的链开头相同，则应该预先减去 96 } 97 }dfs2(1,0);//求树上前缀和（即经过次数） 98 for(register int i=1;i<=(m-(n-1));++i) 99 ans+=num[node[i].first]+num[node[i].second]-2*num[anc[i]]; 100 //开由图可知，两点间路程，应该为a,b的前缀和减去到lca的前缀和 101 printf("%lld",ans); 102 }
然后是一段有注释的倍增求LCA（上面也有，但是没注释），我懒得再开贴子写了，就放在这里吧
1 void dfs1(int u){ 2 //来处理每个点向上走最多2^20次的父亲和每个点的深度 3 for(register int i=1;i<=20;++i) 4 fa[u][i]=fa[fa[u][i-1]][i-1]; 5 //每个点先预处理祖先 6 dep[u]=dep[fa[u][0]]+1;//孩子的深度比爸爸多一 7 for(register int i=head[u];i;i=edge[i].next){ 8 int v=edge[i].to; 9 if(v==fa[u][0]) continue; 10 //如果v正好是u的爸爸，就不用再向上找了 11 fa[v][0]=u; dfs1(v); 12 //如果不是，就代表v的父亲是u(v=edge[i].to),再顺着v向下找 13 } 14 } 15 inline int lca(int u,int v){ 16 //十分正常的求LCA的程序 17 if(dep[u]<dep[v]) swap(u,v); 18 for(register int i=20;i>=0;--i) 19 if(dep[fa[u][i]]>=dep[v]) u=fa[u][i]; 20 //在保证u深度比v大时，向上走，直到两者深度一致 21 if(u==v) return u;//如果正好的话，就返回u 22 for(register int i=20;i>=0;--i) 23 if(fa[u][i]!=fa[v][i]) 24 u=fa[u][i],v=fa[v][i]; 25 //每次让v,u等于2^i的祖先，会快一些，也是倍增的本质（？）吧 26 //跳的步伐先大后小，有利于找的快 27 return fa[u][0]; 28 }