学习方式:
1.了解基本的数学概念 2.了解Unity内的相关内容,加强理解。
第一章:3D数学介绍
1.介绍
•3D数学:研究在3D几何世界中的数学问题。被广泛的应用于使用计算机来模拟3D世界的领域,比如图形学,游戏,虚拟现实和动画等。
•为什么要学习3D数学:掌握了3D数学的知识之后,对我们将来学习图形学、游戏制作都有很大的帮助。
2.1D(数轴)
•3D:three dimensions,立体空间。
•1D:关于计数和度量的数学。
•数学上,数轴是个一维的图,整数作为特殊的点均匀地分布在一条线上。数轴是一条规定了原点、方向和单位长度的直线。
![]()
3.2D(笛卡尔坐标系)
•2D:关于平面的数学。
•数学上,相交的两条直线可以确定一个唯一的平面。相交于原点的两条数轴,构成了平面放射坐标系。
•如果两条数轴上的度量单位相等,则称此放射坐标系为笛卡尔坐标系。
![]()
•数轴互相垂直的笛卡尔坐标系,称为笛卡尔直角坐标系,否则称为笛卡尔斜角坐标系。

•在2D笛卡尔坐标系中,我们用(x,y)来表示一个点。称之为坐标。
•坐标的每个分量都表明了该点与原点之间的距离和方位。每个分量都是到相应轴的有符号距离。

4.3D(空间直角坐标系)
•3D:关于3D空间的数学。
•从2D扩展到3D:相对于2D笛卡尔坐标系,我们需要3个轴来表示三维坐标系,一般叫做空间直角坐标系。
•第3个轴一般被称为z轴。一般情况下,3个轴互相垂直。
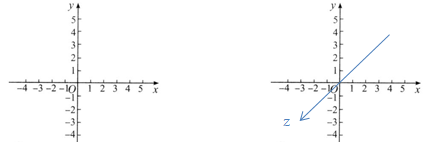
•任意2个轴可以组成一个平面,我们一般称为XY平面,XZ平面,YZ平面,每个平面又与另一个轴相垂直。我们可以认为这3个平面是3个2D笛卡尔空间。
•在3D中,我们用(x,y,z)来表示一个点。坐标的每个分量分别代表了该点到yz,xz,xy平面的有符号距离。
5.左手坐标系与右手坐标系
•z轴方向的确定有2种方式:左手坐标系与右手坐标系。
•左手坐标系:伸开左手,大拇指指向X轴正方向,食指指向Y轴正方向,其他三个手指指向Z轴正方向。
•右手坐标系:伸开右手,大拇指指向X轴正方向,食指指向Y轴正方向,其他三个手指指向Z轴正方向。
•旋转正方向不同:左手坐标系:顺时针。右手坐标系:逆时针。

•3D笛卡尔坐标系:右手坐标系
•OpenGL:右手坐标系
•Direct3D:左手坐标系
•Unity3D:左手坐标系(世界坐标系),即+x, +y, +z分别指向右方,上方和前方。
第二章:Unity中的几种坐标系
1.介绍
•在不同的情况下使用不同的坐标系更加方便,所以在Unity中有多种坐标系:
•1.全局坐标系 World Coordinate System
•2.局部坐标系 Local Coordinate System
•3.屏幕坐标系 Screen Space
•4.视口坐标系 ViewPort Space
2.全局坐标系
•全局坐标系是用于描述场景内所有物体位置的方向的基准,也称为世界坐标系。
•在Unity中创建的物体都是以全局坐标系中的坐标原点(0,0,0),来确定各自的位置的。
•可以使用transform.position来获取游戏对象的世界坐标。
3.局部坐标系
•局部坐标系也称为模型坐标系或物体坐标系。
•每个物体都有自身独立的物体坐标系。当物体移动或改变方向时,和该物体相关联的坐标系将随之移动或改变方向。
•模型Mesh保存的顶点坐标均为局部坐标系下的坐标,这样移动模型时,顶点坐标是不变的。
•transform.localPosition(本地坐标)可以获得物体在父物体的局部坐标系中的位置点。
•父子关系,子物体以父物体的坐标点为自身的坐标原点。
•如果该游戏物体没有父物体,那么transform.localPosition获得的依然是该物体在全局坐标系中的坐标。
•如果该物体有父物体,则获得是在其父物体的局部坐标系中的坐标。
•检视视图中显示的为localPosition的值。
4.屏幕坐标系
•屏幕坐标系是建立在屏幕上的二维坐标系。
•以像素来定义的,屏幕的左下角为(0,0),右上角为(Screen.width, Screen.height),z轴的坐标是相机的世界坐标中z轴坐标的负值。
•鼠标位置坐标属于屏幕坐标,通过Input.mousePosition可以获得该位置的坐标。
•手指触摸屏幕也为屏幕坐标,Input.GetTouch(0).position可以获得单个手指触摸屏幕时手指的坐标。
5.视口坐标系
•视口坐标系是将Game视图的屏幕坐标系单位化,左下角(0,0),右上角(1,1)。z轴的坐标是相机的世界坐标中z轴坐标的负值。
•利用比例可以方便地控制点在屏幕内的位置,而不用理会屏幕的实际大小变化,常用于自适应。
6.坐标系之间的关联与相互转换
•1.全局坐标系和局部坐标系
•关联:
transform.Translate(translation:Vector3, relativeTo: Space = Space.Self);
•沿着translation的方向移动|translation|的距离,其结果将应用到relativeTo坐标系中。如果relativeTo为空,则默认为局部坐标系。【注意】:如果物体本身发生了旋转,局部坐标系和世界坐标系的x轴方向就不一样了。
•转换:
•Transform.TransformPoint(Vector3 position) :将一个坐标点从局部坐标系转换到全局坐标系。
•Transform.InverseTransformPoint(Vector3 position):将坐标点从全局坐标系转换到局部坐标系。
•Transform.TransformDirection(Vector3 direction):将一个方向从局部坐标系转换到全局坐标系。
•Transform.InverseTransformDirection(Vector3 direction):将一个方向从全局坐标系转换到局部坐标系。
•Transform.TransformVector(Vector3 vector):将一个向量从局部坐标系转换到全局坐标系。
•Transform.InverseTransformVector(Vector3 vector):将一个向量从全局坐标系转换到局部坐标系。
•其他:
•Transform.forward, Transform.right, Transform.up:当前物体的物体坐标系的z轴,x轴,y轴在世界坐标系上的指向。
【注意】:使用Translate方法的时候用Space.World,如果默认是Space.Self的话,还要进行一次转换。
•Vector3.forward ,(0,0,1)的缩写。在transform.Translate()中使用时,如果不表明坐标系,则为物体的局部坐标,即物体自身的正前方。
•Vector3.right,(1,0,0)的缩写。•Vector3.up ,(0,1,0)的缩写。
•2.屏幕坐标系与全局坐标系
•转换:
•Camera.ScreenToWorldPoint(Vector3 position): 将屏幕坐标转换为全局坐标。
•Camera.WorldToScreenPoint(Vector3 position):将全局坐标转换为屏幕坐标。
Input.mousePosition:获得鼠标在屏幕坐标系中的坐标
•3.屏幕坐标系与视口坐标系
•转换:
•Camera.ScreenToViewportPoint(Vector3 position):将屏幕坐标转换为视口坐标。
•Camera.ViewportToScreenPoint(Vector3 position):将视口坐标转换为屏幕坐标。
•4.全局坐标系与视口坐标系
•转换:
•Camera.WorldToViewportPoint(Vector3 position):将全局坐标转换为视口坐标。
•Camera.ViewportToWorldPoint(Vector3 position):将视口坐标转换为全局坐标。
第三章:向量的基本概念
1.向量的定义
•在数学中,向量(也称为矢量),是指具有大小和方向的量。
•向量的大小就是向量的长度,也叫做模。向量的方向描述了空间中向量的指向。

•在数学中,书写向量时,通常用方括号将一列数括起来,如[1,2,3]。
•水平书写的向量叫做行向量,垂直书写的向量叫做列向量。上面的向量可以书写成列向量:![]() 。
。
•通常,我们用x,y来代表2D向量的分量,用x,y,z来代表3D向量的分量。
•向量中的数表达了向量在每个维度上的有向位移。

2.点和向量的关系
•点(Point):点中的数表示了一个位置,它没有大小、方向的概念。
•在笛卡尔坐标系,我们可以使用2个或3个实数来表示一个点的坐标。在2D空间中,用P=(Px,Py)来表示一个点的坐标。在3D空间中,用P=(Px,Py,Pz)来表示。

•向量(Vector):向量中的数表示了向量在每个维度上的有向位移。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向。线段长度:代表向量的大小。
•在坐标系中,可以使用v = [x, y]来表示一个2维向量,用v = [x, y, z]来表示一个3维向量。

3.Unity中的点和向量
•在Unity中,只有Vector2、Vector3类型,没有Point2、Point3类型。
•Vector2类型可以用来表示2D向量和点。Vector3类型可以用来表示3D向量和点。
•Transform.position表示一个点,即游戏物体在世界坐标系中的点。
•Transform.forward表示一个向量,即当前物体的物体坐标系的z轴在世界坐标系上的指向。
•在Unity中,点和向量都是以(x,y,z)的形式表示。
•当我们想让游戏物体处于某个位置时,我们可以使用Vector3类型来表示这个点的位置坐标。
•当我们想让游戏物体沿着某个方向以一定的速度移动时,我们可以使用Vector3类型来表示速度的向量值,即速度的大小和方向。
•当我们想计算2个游戏物体之间的距离时,实际上计算的就是以这2个游戏物体为起点和终点的向量的长度。
第四章:向量运算
1.零向量
•零向量是非常特殊的一个向量,它是唯一一个大小为0的向量,也是唯一一个没有方向的向量。
•2D零向量表示为(0,0),3D零向量表示为(0,0,0)。
•在Unity中,用Vector3.zero来表示3D零向量。
2.负向量
•每个向量都有一个负向量,满足条件:一个向量和它的负向量相加等于零向量。
•向量变负,将得到一个和原向量大小相等,方向相反的向量。
•(2,-3,3)的负向量为(-2,3,-3)。即将向量的每个分量都变负。

3.向量的长度
•向量的长度即向量的大小或者向量的模。
•向量的大小就是向量各分量平方和的平方根。
•对2D向量而言,可以构造一个以该向量为斜边,以x,y分量的绝对值为直角边的直角三角形。可以根据勾股定理得到斜边的长度,即向量的长度。

•2D向量的长度: ![]()
•3D向量的长度:![]()
•在Unity中,可以通过Vector3.magnitude计算向量的长度。Vector3.sqrMagnitude则返回向量长度的平方。
•Vector3.Distance(A,B)可以计算2个点A,B之间的距离,即返回向量AB或向量BA的长度。等同于(B-A).magnitude或(A-B).magnitude。
4.向量与标量的乘法/除法
•向量与标量的乘法,即将向量的每个分量分别与标量相乘。
•3D向量与标量相乘:3(1,2,3) = (3,6,9)
•向量与非零标量的除法,即乘以该标量的倒数。
•3D向量与标量相除:
•Unity中使用运算符*来计算与标量的乘法,用运算符/来计算与标量的除法。几何意义:同样方向N倍的位移

5.单位向量
•单位向量也叫做标准化向量,就是大小为1的向量。
•在只关心向量方向,不关心向量大小时,可以使用单位向量,例如求一个面的法线向量时。
•对任意的非零向量,我们都可以计算出它的单位向量,即将其归一化(normalization)。
•向量的归一化:求得向量的长度后,用向量除以它的长度。
•(4,3)归一化后的单位向量为:
•在Unity中,可以使用Vector3.Normalize来归一化向量。使用Vector3.normalized来获得归一化后的单位向量,不改变原有向量。

6.向量的加法/减法
•只有在两个向量的维度相同时,才可以相加或相减。
•向量的加法和减法,即将向量的各个分量相加或相减。
•(1,3)+(2,5) = (1+2,3+5) = (3,8)
•(1,3)-(2,5) = (1-2,3-5) = (-1,-2)
•向量的加法满足交换律:a+b = b+a
•向量的减法则不满足交换律:a-b = -(b-a)
•向量的加法可以理解成平移向量。
•向量的减法则可以理解为平移负向量。
•Unity中,使用运算符+来计算向量的加法。使用运算符-来计算向量的减法。

7.向量的点积
•向量与向量的乘法有两种不同的形式,第一种是向量的点积,也叫做向量的内积。
•表示为a·b,点不可以省略。
•计算时,向量的点积就是对应分量乘积的和,结果为一个标量。
•点积的计算公式为a·b=(ax,ay)·(bx,by)=axbx+ayby
•(0,2)·(3,3) = 0×3+2×3 = 0+6 = 6
•向量的点积满足交换律,即a·b = b·a
•点积的第二种计算方法,则是通过两个向量之间的夹角的cos值。
•a·b = |a||b|cosθ,θ是向量a和向量b的夹角。![]()
•a=(0,2),b=(3,3),两个向量的夹角为45度。
•点乘的结果越大,两向量越相近。通常也被用来求两个向量之间的夹角的大小。

•可以通过向量的点积的结果的符号来判断两个向量的位置关系。
•如果值大于0,则夹角在0度到90度之间(不包含90度),两个向量的方向基本相同。
•如果值等于0,则夹角为90度,两个向量的方向相互垂直。
•如果值小于0,则夹角在90度到180度之间(不包含90度),两个向量的方向基本相反。
•向量的点积还可以用来求得一个向量在另一个向量上的投影。
•向量b在向量a上的投影的长度可以表示为
•向量b在向量a上的投影可以表示为

8.向量的叉积
•两个向量相乘的第二种方式为向量的叉积,也叫做向量的外积。
•表示为a×b,同样,×也不可以省略。
•叉积的结果仍是一个向量。
•叉积仅可应用于3D向量。
•叉积的计算公式为:
a×b=(ax,ay,az)×(bx,by,bz)=(aybz-azby,azbx-axbz,axby-aybx)
•(1,2,3)×(-2,-2,3)=(6-(-6),(-6)-3,(-2)+4)=(12,-9,2)
•叉积得到的向量垂直于原来的两个向量。
•a=(1,2,3),b=(-2,-2,3),a×b=(12,-9,2)。a·(a×b)=0,b·(a×b)=0。
•a×b的长度等于向量的大小与向量夹角的sin值的积,即 ![]() ,也是以a和b为两边的平行四边形的面积的大小。
,也是以a和b为两边的平行四边形的面积的大小。