Fibonacci Numbers
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3117
The Fibonacci sequence is the sequence of numbers such that every element is equal to the sum of the two previous elements, except for the first two elements f0 and f1 which are respectively zero and one.
What is the numerical value of the nth Fibonacci number?
Input
For each test case, a line will contain an integer i between 0 and 10 8 inclusively, for which you must compute the ith Fibonacci number fi. Fibonacci numbers get large pretty quickly, so whenever the answer has more than 8 digits, output only the first and last 4 digits of the answer, separating the two parts with an ellipsis (“...”).
There is no special way to denote the end of the of the input, simply stop when the standard input terminates (after the EOF).
Sample Input
0
1
2
3
4
5
35
36
37
38
39
40
64
65Sample Output
0
1
1
2
3
5
9227465
14930352
24157817
39088169
63245986
1023...4155
1061...7723
1716...7565题目大意:输入n ,输出斐波那契数列第n个 的前4位和后4位,如果不足8位就直接输出
思路:后四位可以直接用矩阵快速幂求,前四位用斐波那契通项公式求,可以先做一下 HDU-1568 是只求前四位
可以先打表求出所有不超过8位的斐波那契数列,通过打表可以发现到39位为止都不超过8位数,当n>39时再分别求前四位和后四位。
由 f(n)=f(n-1)+f(n-2) 构建矩阵:
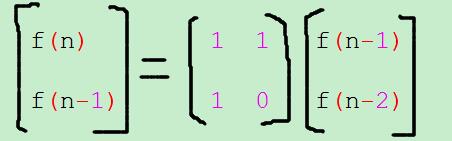
然后矩阵快速幂加取模求f(n)后四位
通项公式:f(n)=1/sqrt(5)(((1+sqrt(5))/2)^n+((1-sqrt(5))/2)^n)
log10 f(n)=-0.5 * log10(5) + n*log10 ( ( 1+sqrt(5) ) /2 ) +log10(1-((1-sqrt(5))/(1+sqrt(5)))^n)
其中当n够大时,log10(1-((1-√5)/(1+√5))^n)无限接近于0,所以可以省略
log10 f(n)=-0.5 * log10(5) + n*log10 ( ( 1+sqrt(5) ) /2 )
令log10(f[n])=a+b,a为整数部分,b为小数部分 a是长度,(int)(10^b*1000)就是前4位
代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
#define mod 10000
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const ll N=2;
int f[50]={0,1,1};
struct Matrix
{
ll a[N][N];
Matrix()
{
mem(a,0);
}
void init()
{
mem(a,0);
for(ll i=0; i<N; i++)
a[i][i]=1;
}
};
void print(Matrix a)
{
for(ll i=0; i<N; i++)
{
for(ll j=0; j<N; j++)
printf("%d ",a.a[i][j]);
puts("");
}
}
Matrix mul(Matrix a,Matrix b)
{
Matrix ans;
for(ll i=0; i<N; i++)
for(ll j=0; j<N; j++)
for(ll k=0; k<N; k++)
{
ans.a[i][j]+=a.a[i][k]*b.a[k][j];
ans.a[i][j]%=mod;
}
return ans;
}
Matrix mat_pow(Matrix a,ll n)
{
Matrix ans;
ans.init();
while(n)
{
if(n&1)
ans=mul(ans,a);
a=mul(a,a);
n>>=1;
}
return ans;
}
int main()
{
for(int i=3;i<=40;i++)
f[i]=f[i-1]+f[i-2];
ll n;
while(~scanf("%lld",&n))
{
if(n<40)
{
printf("%d\n",f[n]);
}
else
{
double cnt=(1.0+sqrt(5.0))/2;
double x=-0.5*log10(5.0)+n*log10(cnt);
x=x-int(x); //取小数部分
x=pow(10.0,x);
x=floor(x*1000); //前四位
Matrix A;
A.a[0][0]=A.a[0][1]=A.a[1][0]=1;
Matrix ans=mat_pow(A,n);
printf("%d...%04lld\n",(int)x,ans.a[0][1]);
}
}
return 0;
}