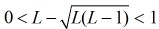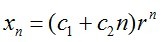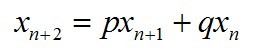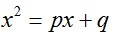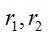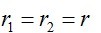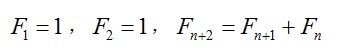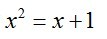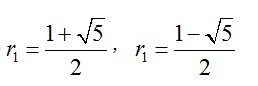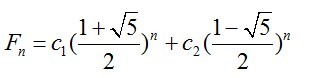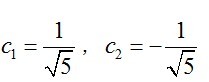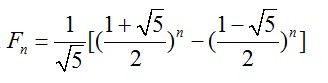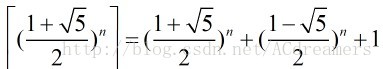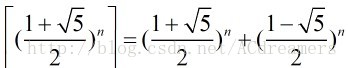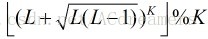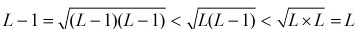A sequence S
n is defined as:

Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S n.
You, a top coder, say: So easy!

Input There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2 15, (a-1) 2< b < a 2, 0 < b, n < 2 31.The input will finish with the end of file. Output For each the case, output an integer S n. Sample Input
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S n.
You, a top coder, say: So easy!
Input There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2 15, (a-1) 2< b < a 2, 0 < b, n < 2 31.The input will finish with the end of file. Output For each the case, output an integer S n. Sample Input
2 3 1 2013 2 3 2 2013 2 2 1 2013Sample Output
4 14 4
#include <iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
/*
发现快速幂虽然会写,但是经常犯一些个错误
1.这个矩阵,到底是怎么样的,次序的问题
[***][f(n-1)] =[ f(n)]
f(n-2) f(n-1)
,那么我们的数据,放置的时候,不要出错,把次序弄乱,特指这个 [f(n-1)] f(n-2)
这直接就是关系到前面的init_martix
2. 经常性的用long long ,但是我们传递参数的时候,经常写成int,不知道是什么原因,
经常性的出错
3.就是到底是 (n-?),取决于你的 f(n-1),这个位置最初放的是谁,f(1),那就n-1,f(2),那就 n-2
4.没有注意,这个init_martix竟然是个负数,所以后面就都错了
*/
ll a,b,n,mod;
struct Martix{
ll mar[2][2];
Martix operator*(Martix& b){
Martix ans;
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
ans.mar[i][j]=0;
for(int k=0;k<2;k++){
ans.mar[i][j]=(ans.mar[i][j]+(mar[i][k]*b.mar[k][j])%mod+mod)%mod;
}
}
}
return ans;
}
}ST,E;
void init(){
memset(E.mar,0,sizeof(E.mar));
E.mar[0][0]=E.mar[1][1]=1;
ST.mar[0][0]=2*a,ST.mar[0][1]=(b-a*a+mod*abs(b-a*a))%mod;
ST.mar[1][0]=1, ST.mar[1][1]=0;
}
Martix pow_(Martix M,ll n){
Martix ans=E;
while(n){
if(n&1) ans=ans*M;
n=n>>1;
M=M*M;
}
return ans;
}
int main()
{
while(scanf("%lld %lld %lld %lld",&a,&b,&n,&mod)==4){
init();
ll t1=(2*(a*a+b))%mod;
ll t2=(2*a)%mod;
if(n==1)
printf("%lld\n",t2);
else{
ST=pow_(ST,n-2);
ll ans=((ST.mar[0][0]*t1)%mod+(ST.mar[0][1]*t2)%mod+mod)%mod;
printf("%lld\n",ans);
}
}
return 0;
}
看到无理数,大家都会很蒙,但是这里是共轭,也就是说,他的相关的项数展开之后,哪些无理数自然就全部笑掉了,关键点就是共轭,下面就是套路了
转自:点击打开链接
利用特征根方程实现通项公式与递推关系的互换
转载一篇博文,学习了!主要运用在矩阵快速幂中,当给了一个通项公式,而n太大时,需要求出其递推关系,这篇文章讲的很好。基本上,只要看见
或者
都是这个套路。
下面是转载
考虑二阶常系数线性齐次递推数列
有方程
该方程称为该数列的特征方程,该方程的两个根称为数列的特征根。
若特征方程有两个不相等的根
则该数列的通项公式为
其中
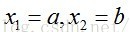
若特征方程有两个相等实根
则该数列的通项公式为
其中
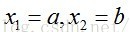
若特征方程有一对共轭复根情况不作要求
所以r1+r2=-b/a=p,r1*r2=c/a=-q;
用特征根求解著名的斐波那契数列,其递推公式为:
其特征方程为
解得
故
将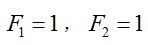
故
ACdreamer的博客:
题目:求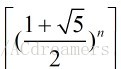
分析:同样的思路,注意是向上取整,所以
当n为奇数时,
当n为偶数时,
题目:已知P=a+b,Q=ab,求a^n+b^n,a,b,n都是正整数。
写出递推式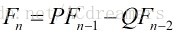
题目:给出K和L,范围都是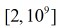
分析:本题是向下取整,它就等于向上取整的结果减1,因为
所以