最大子段和
定义
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n 例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
暴力解法
枚举区间长度,求每一段区间和,维护一个max值
int main()
{
ll n,i,j,k;
scanf("%lld",&n);
for(i = 1;i <= n;i++)
scanf("%lld",&s[i]);
ll maxx = -INF;
for(i = 1;i <= n;i++)
{
for(j = i;j <= n;j++)
{
ll sum = 0;
for(k = i;k <= j;k++)
sum += s[k];
maxx = max(maxx,sum);
}
}
printf("%lld\n",maxx);
return 0;
}动态规划
非负数相加才会使最终得到的区间和变得更大,所以当加上ai后的前缀和 < 0的时候,就不再进行累加,而是重新开始开始记录,这样在最后的数组中得到一个max值就可以。
状态转移:dp[i] = dp[i-1]+s[i]
int main()
{
ll n,i,j,k;
sl(n);
for(i = 1;i <= n;i++)
sl(s[i]);
for(i = 1;i <= n;i++)
{
if(dp[i-1]+s[i] >= 0)
dp[i] = dp[i-1]+s[i];
}
ll maxx = -INF;
for(i = 1;i <= n;i++)
maxx = max(dp[i],maxx);
printf("%lld\n",maxx);
return 0;
}最大m子段和
最大m子段和分为最多选m段,以及最多选m段求最大子段和
动态规划
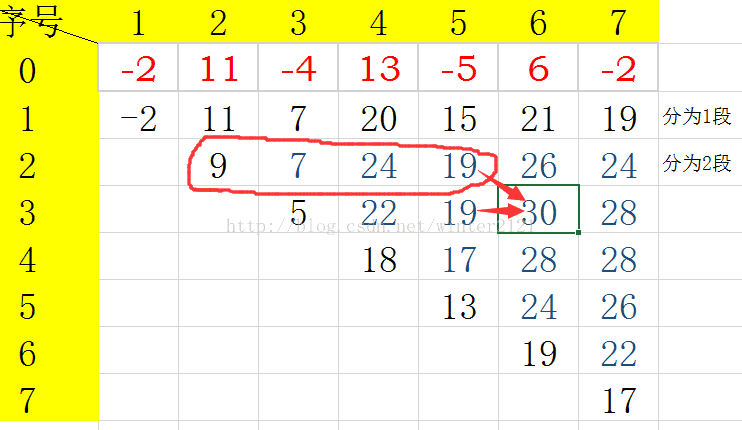
首先,盗图。
初始序列是:-2,11,-4,13,-5,6,-2
可以看到前i项分为i段的最大子段和就是前i项的前缀和
当i大于要分的子段时,对于当前ai的值,可以是它单独作为一个子段也可以是它与前面的子段的结合。
当它作为新的子段加入的时候,它就成为一个需要单独记录的子段,此时子段++
当他作为别的子段的时候,最优方法就是将它加入前面已经分好的最优值的子段中。
对应上面的30这个位置,表示前6个数取3段,得到的最大的和。
若是要得到30,可以通过将前6个数分成3个集合得到的最大值来维护,也可以通过前5项分成2个集合,第6个数单独作为一个集合得到。两者分别是30,25,我们取两者的最大值,得到30.
考虑状态转移方程,dp[i][j] 代表前j个数,分成i个子段的最优值。
则有dp[i][j] = dp[ i ] [ j-1 ] + a[ j ] 表示当前数aj分到前面的序列中,不产生新的序列
dp[i][j] = dp[ i-1 ] [ t ] + a[ j ] 表示分i-1个集合,aj作为新的集合产生的最优值
优化
当前状态只与前一行的状态有关,可以滚动数组来实现
求前一行的max值,可以在对j的遍历中得到前一行的最大值
只求上三角的矩阵
例题
Max Sum Plus Plus
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 39525 Accepted Submission(s): 14218
Problem Description
Now I think you have got an AC in Ignatius.L's "Max Sum" problem. To be a brave ACMer, we always challenge ourselves to more difficult problems. Now you are faced with a more difficult problem.
Given a consecutive number sequence S1, S2, S3, S4 ... Sx, ... Sn (1 ≤ x ≤ n ≤ 1,000,000, -32768 ≤ Sx ≤ 32767). We define a function sum(i, j) = Si + ... + Sj (1 ≤ i ≤ j ≤ n).
Now given an integer m (m > 0), your task is to find m pairs of i and j which make sum(i1, j1) + sum(i2, j2) + sum(i3, j3) + ... + sum(im, jm) maximal (ix ≤ iy ≤ jx or ix ≤ jy ≤ jx is not allowed).
But I`m lazy, I don't want to write a special-judge module, so you don't have to output m pairs of i and j, just output the maximal summation of sum(ix, jx)(1 ≤ x ≤ m) instead. ^_^
Input
Each test case will begin with two integers m and n, followed by n integers S1, S2, S3 ... Sn.
Process to the end of file.
Output
Output the maximal summation described above in one line.
Sample Input
1 3 1 2 3
2 6 -1 4 -2 3 -2 3
Sample Output
6 8
Hint
Huge input, scanf and dynamic programming is recommended.
代码实现:
/*
Look at the star
Look at the shine for U
*/
#include<bits/stdc++.h>
#define ll long long
#define PII pair<int,int>
#define sl(x) scanf("%lld",&x)
using namespace std;
const int N = 1e6+5;
const int mod = 1e9+7;
const int INF = 0x3f3f3f3f;
const double PI = acos(-1);
ll inv(ll b){if(b==1)return 1; return (mod-mod/b)*inv(mod%b)%mod;}
ll fpow(ll n,ll k){ll r=1;for(;k;k>>=1){if(k&1)r=r*n%mod;n=n*n%mod;}return r;}
ll s[N],dp[2][N];
int main()
{
ll n,i,j,k,m;
while(~sl(m))
{
sl(n);
for(i = 1;i <= n;i++)
sl(s[i]);
for(i = 0;i <= n;i++)
dp[0][i] = dp[1][i] = 0;
ll maxx;
for(i = 1,k = 1;i <= m;i++,k ^= 1)
{
dp[k][i-1] = -INF;
maxx = -INF;
for(j = i;j <= n-m+i;j++)
{
maxx = max(dp[k^1][j-1],maxx);
dp[k][j] = max(dp[k][j-1],maxx)+s[j];
}
}
ll ans = -INF;
for(i = m;i <= n;i++)
ans = max(ans,dp[m&1][i]);
printf("%lld\n",ans);
}
return 0;
}