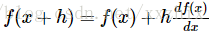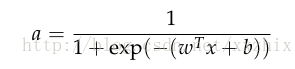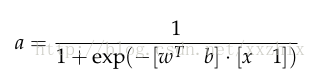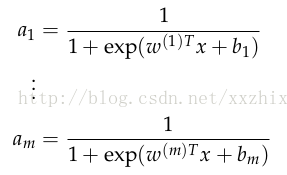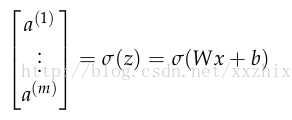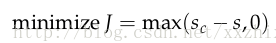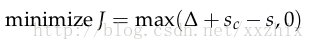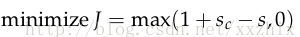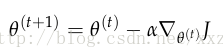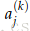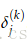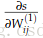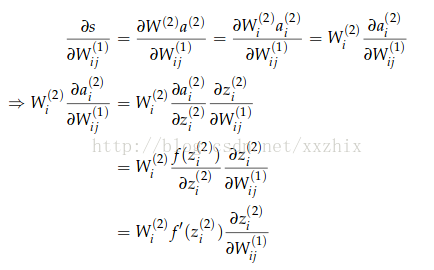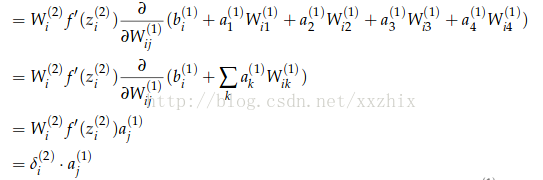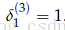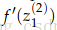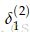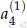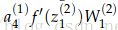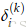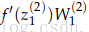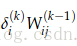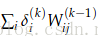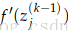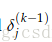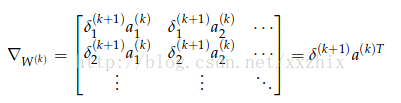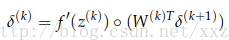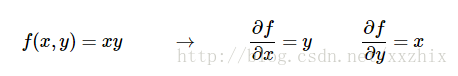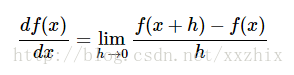这是很早之前看到的cs224n lecture note 3中一篇文章,当时翻译了一部分,没有翻译完,现在好像找不到了。觉得这篇文章对理解后向传播很有用,分享一下。如有问题,还望大家指出,非常感谢!
这部分介绍单层和多层神经网络,以及它们如何用于分类,并介绍如何使用分布的梯度下降(distributed gradient decent),也就是backpropagation来训练这些模型。在训练过程中,参数利用链式规则顺序更新。
1.神经网络:基础
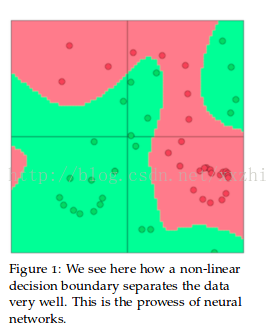
由于大多数数据都不是线性可分的,因此线性分类器的效果有限,使用非线性分类是有必要的。神经网络是非线性决策边界的一类分类器,如图。
1.1 一个神经元
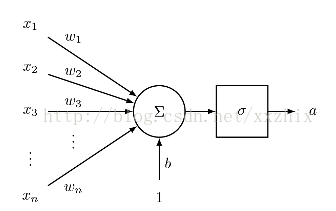
一个神经元是接受n个输入,提供1个输出的通用的计算单元,不同神经元的输出不同区别在于它们的参数,也就是权重。神经元通用的选择是“sigmoid”或者二分类逻辑回归函数。这类神经元接受n维的输入向量x,提供标量激活输出a。这类神经元和n维的权重向量w和一个偏移标量b有关,神经元的输出如下:
我们也可以将权重和偏移统一,变成以下这个等价的表达式:
这个式子可以用下图来形象说明
1.2 单层神经网络
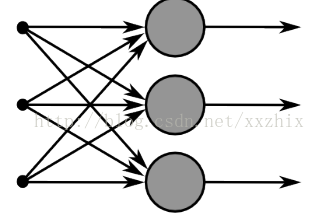
接下来考虑多个神经元的情况,也就是同一个x作为多个神经元的输入,下图中同一个x作为3个神经元的输入:
如果将m个不同神经元的权重记为{w(1),w(2),...w(m)}和偏移{b1,b2...bm},各自的激活值是{a1,a2,..am},则
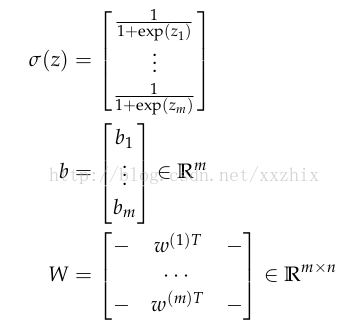
定义以下抽象化的表示,使得表达式简单,并能用于更多的复杂的神经网络:
那么,进行标量化和加入偏移之后的输出可以写成
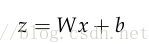
sigmoid的激活值(activation)可以写成
但这些激活值可以告诉我们什么呢?可以认为这些激活值作为衡量某些特征的加权组合是否会出现的指标,然后利用这些激活值的组合进行分类。
1.3 前馈计算
我们已经知道了如何将输入x放入sigmoid函数获得激活值输出,但我们为什么要这么做呢?考虑以下NLP中的一个实体识别问题作为例子:
“Museums in Pairs are amazing”
我们想要判断中间的词'Pairs'是不是命名实体(named-entity)。在这个例子中,我们很可能不止想知道这个词周围出现的词,还有这些词之间的其他关联,从而做出分类。例如,可能“Museum”这个词是第一个词对分类有用,当且仅当“in”是第二个词。这种非线性的决策通常不能通过简单地将输入直接放入Softmax函数,而是需要中间层来评分。因此,我们可以使用另一个矩阵U来由激活值生成一个用于分类的非标准化得分:
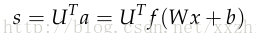
维数的分析:如果每个单词我们使用一个4维的词向量,5个单词的窗口(即这个词周围5个词)作为输入,那输入x就是20维。如果我们在隐藏层使用8个sigmoid神经元,输出一个得分,那W(8*20),b(8),U(8*1)。
1.4 最大边界目标函数
神经网络也需要优化目标,用来衡量我们想要最小化的误差或者最大化的正确(goodness)。这里,我们讨论常用的一种误差矩阵,最大边界目标。使用这种目标函数的背后的想法是保证正类数据点的得分比负类数据点的得分高。
用之前命名实体识别的例子,如果我们将正类的例子“Museums in Pairs are amazing”的得分记为s,负类标签“Not all museums in Pairs”的得分记为sc。(这里为什么第一句是正类样本,第二句是负类样本,我也不是很懂,希望赐教)
然后,我们的目标函数就是要最大化(s-sc)或最小化(sc-s)。我们修改目标函数来保证误差只有在sc>s,也就是sc-s>0的时候才被计算。这么做是因为我们只关心正类数据点比负类数据点的得分高,其他不关心。因此,我们的误差是(sc-s),如果sc>s,否则就是0。
但是,上面这个最优化目标有点冒险,因为它没有试着建立一个安全的区域。我们想要正类的的得分比负类的得分大一个正区间d。换句话说,当(s-sc)<d时,计算误差,当(s-sc)>d,是,不计算误差。(原文中是说s<sc时,不计算误差,我觉得这边应该是s-sc>d时不计算误差。如果这边理解错了,请随时指正,非常感谢)修改优化目标为:
我们能够按比例缩减这个区间使得d=1,使在这个最优化问题中的其他参数同样调整。
最后,我们定义以下最优化目标,将用训练集来优化:
在上式中,,
。
1.5 后向传播(backpropagation)--elemental
如1.4节讨论的代价函数,当代价函数为正时,我们需要训练参数,当代价为0时,不需要更新参数。由于通常使用梯度下降来更新参数,如下式,需要参数的梯度信息:
后向传播(backpropogration)是一种是能使用导数的链式法则来计算所有在前馈计算中用到的参数的损失梯度的方法。
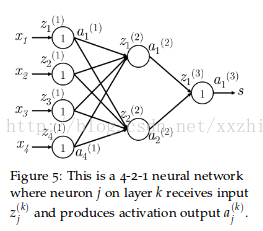
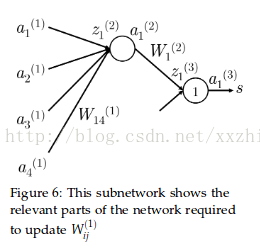
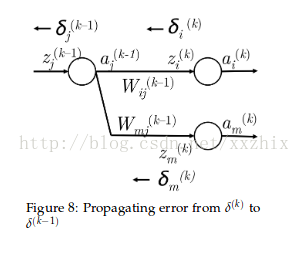
以下图的神经网络来说明后向传播。
定义一些符号:
xi是神经网络的输入
s是神经网络的输出
每层(包括输入和输出层)有神经元接受输入并提供输出。第k层的第j个神经元接受标量输入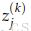
在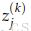
第1层是指输入层,不是指第一个隐藏层。对输入层来说,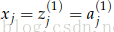
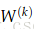
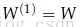
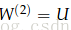
现在开始后向更新参数的过程:
假设代价函数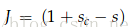
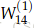
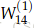
由上图可以看出,
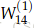
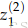
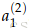
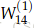
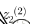
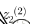
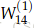
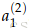
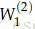
下面计算
说明:第2个等号是因为wij(1)之后ai(2)有关,和其他不等于i的j的aj(2)无关
梯度被化简为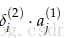
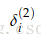
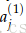
以Figure 6为例讨论错误分享或错误分布的解释。以更新参数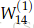
1.从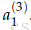
2.然后把这个错误乘以从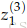
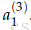
3.现在,错误信号到了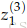
4.到达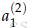
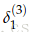
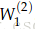
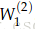
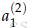
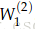
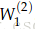
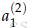
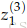
5.就像第2步一样,需要错误信号穿过使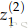
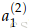
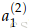
6.在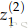
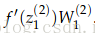
7.最后,需要将错误信号公平的分摊到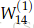
8.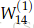
可以发现,通过这种方法得到的梯度值和使用导数得到的一样。
所以,在计算后向更新的梯度值时,可以使用导数,也可以使用错误分享的这种过程。结果是一样的,但可以帮我们从不同的角度思考。
偏移更新:
偏移更新和其他到达同一个值的权重的更新在计算上是一样的,只是向前的输入是1。
因此,第k层第i个神经元的偏移梯度是
例如,要更新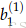
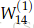
从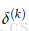
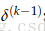
1.有从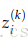
2.将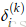
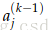
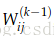
3.因此,到达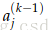
4.但是,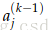
5.因此,节点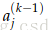
6.一般化为
7.有了在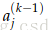
8.因此,到达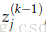
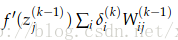
1.6 后向传播的训练--向量化
至今为止,我们讨论了如何计算模型中某个参数的梯度,现在将这种方法一般化,使能够一次更新权重矩阵和偏移向量。这只是上述模型的简单延伸为了能在矩阵和向量的基础上进行错误的后向传播。
对给定的一个参数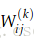
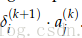
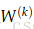
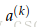
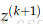
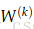
整个矩阵的梯度可以写成到达这个矩阵的后向错误和这个矩阵向前计算的激活值的矩阵的乘积。
现在来看怎么计算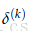
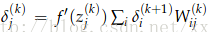
式子中的圈圈运算符是指两个向量对应元素相乘。
计算效率:在看过单个参数的更新和基于向量的更新之后,在科学计算环境中,向量运算更快,所以,实际计算中,使用向量。
同时,我们也需要减少多余的计算,例如: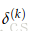
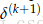
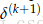
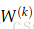
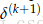
2. 技巧
下面探讨一些神经网络实际应用中的技巧。
2.1 梯度建议
在上面最后一部分,我们探讨了如何用代数方法计算神经网络中的错误梯度。现在介绍一种在数值上约等于梯度的技术,尽管这种方法计算效率太低不能直接训练网络,但是我们能很准确地估计任何参数的导数。因此,这种方法可以检验我们计算的导数值是否正确的方法。
假设模型的参数向量为θ,损失函数为J,
从计算图的角度理解后向传播
从简单开始,考虑乘法函数f(x,y)=x*y,每个输入的偏导数可以按以下计算式简单计算:
导数能告诉我们什么呢?导数表明了相对于某个变量在某个取值附近很小很小的区域内变化,整个函数变化的比例。
上式左边的除号和右边的除号不同,右边的除号是相除的意思,左边的意思是将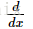
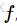
一种比较好的理解上面式子的方式是,当h很小时,函数可以用一条直线来近似,而导数是直线的斜率。也就是说,每个变量的导数说明了整个表达式对变量的敏感度。
例如,假如x=4,y=-3,那么f(x,y)=x*y=-12,x的导数值为-3。就是说,如果我们将x增加一个很小的值,那么整个表达式会减小,并且是减少x的变化值的3倍。可以将上式进行等式变换为