LeetCode 132 Palindrome Partitioning II

问题描述：

解答：

这个问题可以抽象成一个DP问题，对于一个长度为n的字符串，设DP[i][j]表示第i个字符到第j个字符是否构成回文，若是，则DP[i][j]=1;若否，则DP[i][j]=0;如此，根据回文的约束条件（对称性），DP[i][j]构成回文需满足：

1、输入字符串s[i]==s[j],对称性；

2、条件1满足并不能保证i到j构成回文，还须：（j-i）<=1或者DP[i+1][j-1]=1；即，i、j相邻或者i=j，也就是相邻字符相等构成回文或者字符自身构成回文，如果i、j不相邻或者相等，i到j构成回文的前提就是DP[i+1][j-1]=1.

所以状态转移方程：DP[i][j]=(s[i]==s[j]&&(j-i<=1||DP[i+1][j-1]==1))。由于i必须小于j，i>=0&&i<s.length().如此，DP[i][j]构成一个下三角矩阵，空间、时间复杂度均为O(n2),如下所示：对于长度为4的字符串s=“baab”，其中红色部分为i>j，为无意义部分；绿色部分i==j，即字符串自身必然构成回文，DP[i][j]=1;白色部分，为长度大于1的子串，需要状态转移方程进行判断。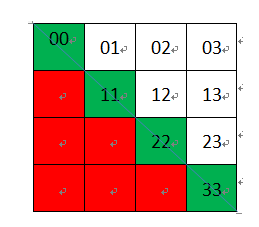


public longestPalindrome_1(String s) 
	{
        int [][] dp=new int[s.length()][s.length()];//存储状态变量，初始化为0
        for(int i=s.length()-1;i>=0;i--)
        {
        	for(int j=i;j<s.length();j++)
            {
                if(s.charAt(i)==s.charAt(j)&&(j-i<=1||dp[i+1][j-1]==1))//状态转移方程
                {
                    dp[i][j]=1; //可进行回文分割，则置为1
                }
            }
        }   
    }

经过判断，得到状态矩阵：绿色部分，即字符串“baab”可构成的回文子串分割情况：绿色部分DP[0][0]、DP[1][1]、DP[2][2]和DP[3][3]构成的是单字符回文子串，DP[1][2]和DP[0][3]构成的是多字符回文子串。

在得到输入字符串的所有回文子串的分割情况之后，我们需要考虑如何求取回文子串的最小分割次数，显然，回文子串越长，分割次数越少，因此，分割的时候回文子串应分别取最大长度，如上面的例子，s="baab"，可行的分割情况有三种：（显然，最少分割次数为0，当然，根据DP[][]矩阵可以很容易求取最长回文子串！！！！）。

1、{DP[0][0]、DP[1][1]、DP[2][2]、DP[3][3]}；

2、{DP[0][0]、DP[1][2]、DP[3][3]}；

3、{DP[0][3]}

当输入字符串所有可能的分割情况求出来之后，我们需要进一步寻找最少分割次数，我们可以用一个一维数组来存储分割次数：设int[] cut=new int[s.length()+1],cut[i]表示第i个字符到最后一个字符所构成的子串的最小分割次数，这里的i有约束条件，就是第i个位置必须是可进行回文分割的，即DP[i][j]==1 (j>=i&&j<s.length()),故：

根据这个公式，我们最终要求的cut[0]与cut[0]、cut[1]...cut[len]都有关，直接求需要递归，效率低，因此我们可以逆序求解，即：先求cut[len-1]，最后求cut[0].

在原作者思路上改进了一下细节。

len[s.length()]=-1;//trick

为了初始化len[s.length-1]=0

初始化

len[i]=s.length()-1;

比如 abab 砍4-1=3次肯定可以

原作者源码：

public class Solution {
    public int minCut(String s) {
        int [][] dp=new int[s.length()][s.length()];
        int [] cut=new int[s.length()+1];
        
        for(int i=s.length()-1;i>=0;i--)
        {
            cut[i]=Integer.MAX_VALUE;
        	for(int j=i;j<s.length();j++)
            {
                if(s.charAt(i)==s.charAt(j)&&(j-i<=1||dp[i+1][j-1]==1))
                {
                    dp[i][j]=1;
                    cut[i]=Math.min(1+cut[j+1],cut[i]);  
                }
            }
        }
        return cut[0]-1;  
    }

}

本人源码：

class Solution {
    public int minCut(String s) {
        int[][] dp=new int[s.length()][s.length()];
        int[]len=new int[s.length()+1];
        len[s.length()]=-1;//trick
        for(int i=s.length()-1;i>=0;i--){
            len[i]=s.length()-1;
            for(int j=i;j<s.length();j++){
                if((s.charAt(i)==s.charAt(j)) && (j-i<=1||dp[i+1][j-1]==1)){
                    dp[i][j]=1;
                    len[i]=Math.min(len[i],1+len[j+1]);//len[s.length()]=-1;初始化len[s.length-1]=0
                }
            }
        }
        return len[0];
    }
}

---------------------

原文：https://blog.csdn.net/jin_kwok/article/details/51423222

LeetCode 132 Palindrome Partitioning II

猜你喜欢