Matlab学习笔记（三）

主要内容（大概）

一、复习积分、级数
二、泰勒级数和傅里叶级数
三、Matlab求解 —— 微分和代数

目录

积分复习

级数复习

泰勒级数

傅里叶级数

Matlab求解微分方程

积分复习 ↶

1.quad做无穷（广义）有点问题，int比较精确，用int最好，下面的例子用来对比：
例，计算下列广义积分
$\int_{-\infty }^{\infty}e^{cosx-x^{2}}dx$

clear
format long
syms x %为int做准备
ff = @(x)(exp(cos(x)-x.^2)); %定义匿名函数，可以用inline
y1 = quad(ff, -inf, inf)
y2 = quad(ff, -100, 100)
y3 = quad(ff, -1e10, 1e10)
y4 = quadl(ff, -1e20, 1e20)
y5 = vpa(int(exp(cos(x)-x.^2), -inf, inf), 15)

y1 =  NaN
y2 = 3.989813604029027
y3 = 3.989812541283583
y4 = 25.814543367399441 %精度的范围导致的结果变化
y5 = 3.989812272586 %用vpa控制精度产生的结果

2.quad/quadl（精度问题）优化程序
优化程序：

clear;
ff = @(x)(exp(cos(x)-x.^2));
n = 10; m = 2; c = 1e-6; a = inf; % n为上下限，m控制步长，c指定精度，a为辅助变量
b = quadl(ff, -n, n);
while abs(a-b) > c;
a = b; n = n*m;
b = quadl(ff, -n, n);
end

级数复习 ↶

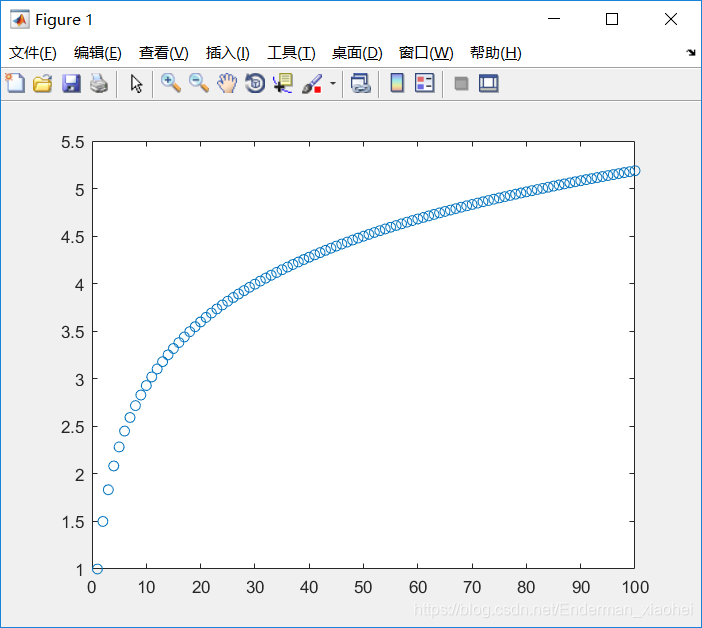
应用一：Euler常数的发现
$\gamma = \lim_{n\rightarrow \infty }(\sum_{i=1}^{n}\frac{1}{i}-ln(n))$
1.观察调和级数部分和数列的规律

clear;
syms m
for n=1:100;
a(n) = symsum(1/m, m, 1, n);
end
plot([1:n], a, 'o')

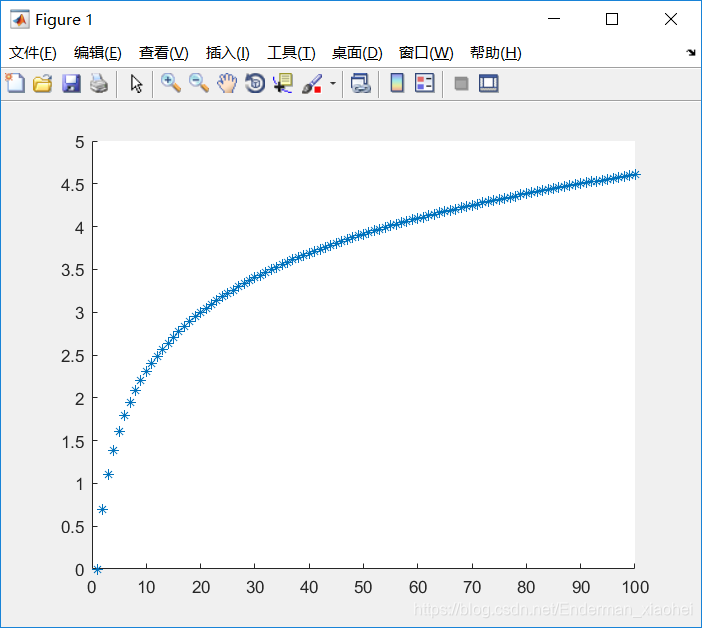
2.画图比较与对数函数的差异

hold on
for n=1:100;
b(n) = log(n);
end
plot([1:n], b, '*')

泰勒级数 ↶

应用二：Taylor幂级数展开
例：计算cos(2x)泰勒x=4处展开式的前6项
第一步：编辑Ty.m函数文件

function y = Ty(fun, a, n)
syms x
c = subs(fun, x, a); %用a替换x
for k=1:n
funk = subs(diff(fun, k), x, a);
c = [c, funk]; %有加法的感觉，把funk放入c中， c = 0; funk = 1; c += funk
end
d = 1;
for k=1:n
d = [d, (x-a)^k/factorial(k)]; %同理
end
md = c.*d; %两者相乘
y = sum(md, 2); %对md的每行分别求和

第二步：命令窗口输入

syms x
fun = cos(2*x)
Ty(fun, 4, 5)

结果：

fun = cos(2*x)
ans = cos(8) + (4*sin(8)*(x - 4)^3)/3 - (4*sin(8)*(x - 4)^5)/15 - 2*sin(8)*(x - 4) - 2*cos(8)*(x - 4)^2 + (2*cos(8)*(x - 4)^4)/3

Talylor幂级数展开

syms x
taylor(fun, x, 'ExpansionPoint', x0, 'order', n)
%或者
taylor(fun, x, x0, 'order', n)
%幂级数
taylor(fun, x, n)

例： $f(x)=\frac{sinx}{x^2+4x+3}$，求其Taylor幂级数展开前9项，并求关于x=2和x=a进行Taylor幂级数展开

syms x;
f = sin(x)/(x^2+4*x+3);
y1 = taylor(f, x, 9) 
%结果
y1 = sin(9)/120 + (x - 9)*(cos(9)/120 - (11*sin(9))/7200) - (x - 9)^2*((11*cos(9))/7200 + (1709*sin(9))/432000) - (x - 9)^3*((509*cos(9))/432000 - (19129*sin(9))/25920000) + ((58051*cos(9))/1555200000 - (4763231*sin(9))/93312000000)*(x - 9)^5 + ((5929*cos(9))/25920000 + (380851*sin(9))/1555200000)*(x - 9)^4

x = 2时：

syms x;
f = sin(x)/(x^2+4*x+3);
y1 = taylor(f, x, 2, 'order', 9)
%结果
y1 = sin(2)/15 - ((131623*cos(2))/35880468750 + (875225059*sin(2))/34445250000000)*(x - 2)^8 + (x - 2)*(cos(2)/15 - (8*sin(2))/225) - ((623*cos(2))/11390625 + (585671*sin(2))/2733750000)*(x - 2)^6 + ((262453*cos(2))/19136250000 + (397361*sin(2))/5125781250)*(x - 2)^7 - (x - 2)^2*((8*cos(2))/225 + (127*sin(2))/6750) + (x - 2)^3*((23*cos(2))/6750 + (628*sin(2))/50625) + (x - 2)^4*((28*cos(2))/50625 - (15697*sin(2))/6075000) + (x - 2)^5*((203*cos(2))/6075000 + (6277*sin(2))/11390625)

x = a时；

syms x a;
f = sin(x)/(x^2+4*x+3);
y1 = taylor(f, x, a, 'order', 9)
%结果
y1 = sin(a)/(a^2 + 4*a + 3) - (a - x)^2*(sin(a)/(2*(a^2 + 4*a + 3)) + (cos(a)*(2*a + 4))/(a^2 + 4*a + 3)^2 - (sin(a)*((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)) - (cos(a)/(a^2 + 4*a + 3) - (sin(a)*(2*a + 4))/(a^2 + 4*a + 3)^2)*(a - x) - (a - x)^6*(sin(a)/(720*(a^2 + 4*a + 3)) - (sin(a)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(2*(a^2 + 4*a + 3)) + (cos(a)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(6*(a^2 + 4*a + 3)) + (cos(a)*(2*a + 4))/(120*(a^2 + 4*a + 3)^2) - (sin(a)*((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3)))/(24*(a^2 + 4*a + 3)) - (sin(a)*((((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3) + (cos(a)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)) - (a - x)^7*((sin(a)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(2*(a^2 + 4*a + 3)) - cos(a)/(5040*(a^2 + 4*a + 3)) + (cos(a)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(6*(a^2 + 4*a + 3)) + (sin(a)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(24*(a^2 + 4*a + 3)) + (cos(a)*((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3)))/(120*(a^2 + 4*a + 3)) + (cos(a)*((((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3) + (sin(a)*(2*a + 4))/(720*(a^2 + 4*a + 3)^2) + (sin(a)*((((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*((((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)) - (a - x)^3*((sin(a)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3) - cos(a)/(6*(a^2 + 4*a + 3)) + (cos(a)*((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3) + (sin(a)*(2*a + 4))/(2*(a^2 + 4*a + 3)^2)) + (a - x)^5*((sin(a)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3) - cos(a)/(120*(a^2 + 4*a + 3)) + (cos(a)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3) + (sin(a)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(2*(a^2 + 4*a + 3)) + (cos(a)*((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3)))/(6*(a^2 + 4*a + 3)) + (sin(a)*(2*a + 4))/(24*(a^2 + 4*a + 3)^2)) + (a - x)^4*(sin(a)/(24*(a^2 + 4*a + 3)) - (sin(a)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3) + (cos(a)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3) + (cos(a)*(2*a + 4))/(6*(a^2 + 4*a + 3)^2) - (sin(a)*((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3)))/(2*(a^2 + 4*a + 3))) + (a - x)^8*(sin(a)/(40320*(a^2 + 4*a + 3)) - (sin(a)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(24*(a^2 + 4*a + 3)) + (cos(a)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(120*(a^2 + 4*a + 3)) + (cos(a)*(2*a + 4))/(5040*(a^2 + 4*a + 3)^2) - (sin(a)*((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3)))/(720*(a^2 + 4*a + 3)) - (sin(a)*((((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(2*(a^2 + 4*a + 3)) - (sin(a)*(((((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*((((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3) + (cos(a)*((((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*((((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3) + (cos(a)*(((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) - ((2*a + 4)*(((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))/(a^2 + 4*a + 3) + ((2*a + 4)*((2*a + 4)/(a^2 + 4*a + 3)^2 - (((2*a + 4)^2/(a^2 + 4*a + 3)^2 - 1/(a^2 + 4*a + 3))*(2*a + 4))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(a^2 + 4*a + 3)))/(6*(a^2 + 4*a + 3)))

傅里叶级数 ↶

应用三：Fourier级数展开
例：求下述分段函数在[-π, π]的傅里叶级数的前2m+1项和
$y=\begin{cases} 0 ,-\pi \leq x< 0& \text{ } \\ 1, 0 \leq x< \pi& \text{ } \text{ } \end{cases}$
1）编写f_1.m函数文件

function y = f_1(x)
y = (x>=0&x<pi) + (x>=2*pi&x<3*pi); %为画图准备

2）编写f2_series.m函数文件

function S = f2_series(fun, L, m)
syms x
a0 = (int(fun(1), x, -L, 0) + int(fun(2), x, 0, L))/L;
ssn=0;
for k=1:m
ak = (int(fun(1)*cos(k*pi*x/L), x, -L, 0) + int(fun(2)*cos(k*pi*x/L), x, 0, L))/L;
bk = (int(fun(1)*sin(k*pi*x/L), x, -L, 0) + int(fun(2)*sin(k*pi*x/L), x, 0, L))/L;
sk = ak*cos(k*pi*x/L) +bk*sin(k*pi*x/L);
ssn = ssn + sk;
end
S = ssn + a0/2; 

3）命令窗口输入

clear
syms x
fun = [0, 1];
f2_series(fun, pi, 19)
%结果
ans = (2*sin(3*x))/(3*pi) + (2*sin(5*x))/(5*pi) + (2*sin(7*x))/(7*pi) + (2*sin(9*x))/(9*pi) + (2*sin(11*x))/(11*pi) + (2*sin(13*x))/(13*pi) + (2*sin(15*x))/(15*pi) + (2*sin(17*x))/(17*pi) + (2*sin(19*x))/(19*pi) + (2*sin(x))/pi + 1/2

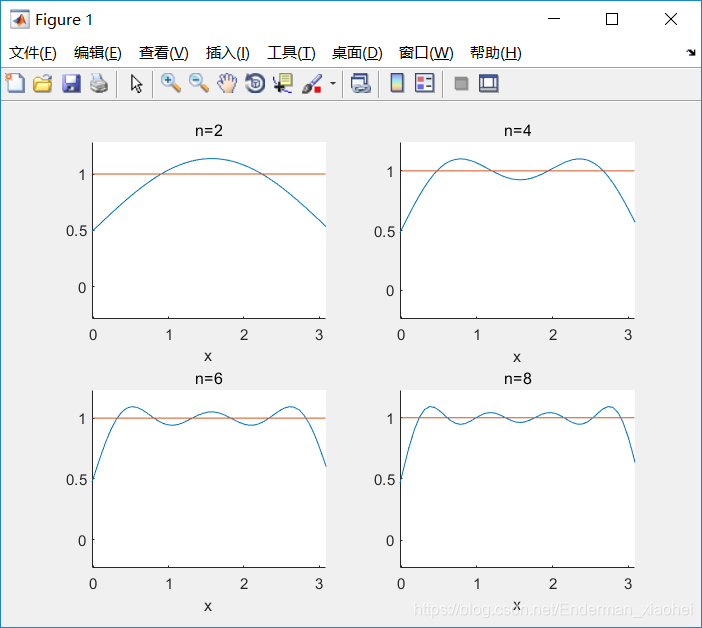
4)观察逼近效果

syms x
f = [0, 1]; p = 2;
for k=1:4
fkp = f2_series(f, pi, k*p);
subplot(2, 2, k); hold on; ezplot(fkp); ezplot('f_1'); title(['n=', int2str(k*p)]);
end

Matlab求解微分方程 ↶

微分方程的解析解——通解
求微分方程（组）的解析解命令：
dsolve('方程1', '方程2', ..., '方程n', '初始条件', '自变量')
注：如果初始条件省略，则表示求通解
自变量可以指定或由系统规则选定为缺省（缺省为t）
例1：求下述微分方程的通解（解析解），并验证
$\frac{\mathrm{d}u}{\mathrm{d} x}=1+u$
（1）输入命令

u = dsolve('Du = 1 + u', 't')

% 结果
u = C4*exp(t) - 1

（2）验证：

syms t
diff(u, t) - u - 1

% 结果
ans = 0

在表达微分方程时，D后所跟的字母为因变量，整体表示对自变量的导数，如：
$Du\rightarrow {u}', Du\rightarrow {u}'', Du\rightarrow {u}'''$
显示解析解没有，返回隐式解
例2：求下述微分方程的通解
$(y^4-3x^2)dy+xydx=0$
1）尝试：

dsolve('(y^4-3*x^2)*Dy + x*y = 0', 'x')
% 结果
ans = x^(1/2)*root(z^3 - z^2*exp(2*C6 - log(x)) + exp(2*C6 - log(x)), z, 1)^(1/2)
                                                                           0
                                                                     x^(1/2)
                                                                    -x^(1/2)
                                                                  x^(1/2)*1i
                                                                 -x^(1/2)*1i

2）交换变量x, y

dsolve('x*y*Dy + x^4 - 3*y^2 = 0', 'x')
% 结果 
ans =   (x^4*(C8*x^2 + 1))^(1/2)
       -(x^4*(C8*x^2 + 1))^(1/2)

3）换回x，y，得：
$x^2=y^4+Cy^6$
线性微分方程组的通解
例2：求下述微分方程组的通解
$\begin{cases} \frac{\mathrm{d}x }{\mathrm{d} t}=2x-3y+3z & \text{ } \\ \frac{\mathrm{d}y }{\mathrm{d} t}=4x-5y+3z& \text{ } \\ \frac{\mathrm{d}z }{\mathrm{d} t}=4x-4y+2z& \text{ } \end{cases}$
输入命令：

[x, y, z] = dsolve('Dx = 2*x - 3*y + 3*z', ... %...是续行符
					'Dy = 4*x - 5*y + 3*z', ...
					'Dz = 4*x - 4*y + 2*z', ...
					't')
					
%结果
x = C9*exp(2*t) + C10*exp(-t)
y = C9*exp(2*t) + C10*exp(-t) + C11*exp(-2*t)
z = C9*exp(2*t) + C11*exp(-2*t)

或者

r = dsolve('Dx = 2*x - 3*y + 3*z', ... %...是续行符
					'Dy = 4*x - 5*y + 3*z', ...
					'Dz = 4*x - 4*y + 2*z', ...
					't')
%返回结构型数据r					
%结果
r =  包含以下字段的 struct: 
    y: [1×1 sym]
    x: [1×1 sym]
    z: [1×1 sym]

%提取
>> r.x
ans = C9*exp(2*t) + C10*exp(-t)
>> r.y
ans = C9*exp(2*t) + C10*exp(-t) + C11*exp(-2*t)
>> r.z 
ans =  C9*exp(2*t) + C11*exp(-2*t)

例3：求下述微分方程组的特解
$\begin{cases} \frac{\mathrm{d^2}y }{\mathrm{d} x^2}+4\frac{\mathrm{d} y}{\mathrm{d} x}+29y=0& \text{ } \\y(0)=0, {y}'(0)=15& \text{ } \text{ } \end{cases}$
输入命令：

y = dsolve('D2y + 4*Dy + 29*y = 0', 'y(0) = 0', 'Dy(0) = 15', 'x')
% 'D2y + 4*Dy + 29*y = 0'：微分方程
% 'y(0) = 0'：cond1
% 'Dy(0) = 15' cond2
% 'x' var
%结果
y = 3*sin(5*x)*exp(-2*x)

用Matlab软件求常微分方程的数值解
[t, x] = solver('f', ts, x0, options)

1. t：自变量值
2. x：函数值
3. solver：ode45；ode23；ode113；ode15s；ode23s
   ode23：组合的2/3阶龙格-库塔-分尔格算法
   ode45：运用组合的4/5阶龙格-库塔-分尔格算法
4. ‘f’：由待解方程写成m-文件名
5. ts：ts = [t0, tf]，t0，tf为自变量的初值和终值
6. x0：函数的初值
7. options：用于设定误差限（缺省时设定为相对误差10^-3，绝对误差10^-6）,
   命令为：options = odeset(‘reltol’, rt, ‘abstol’, at)
   其中rt，at分别为设定的相对误差和绝对误差。

注意：

1. 在解n个未知数的方程组时，x0和x均为n维向量，且m-文件中的待解方程组应以x的分量形式写成。
   [t, x] = solver('ODE函数', [t0, tf], x0, options)
   输出变量形式为：
   $t=\begin{bmatrix}t_{0} \\ t_{1} \\ t_{2} \\ . \\ . \\ . \end{bmatrix}, x=\begin{bmatrix} x_1(t_0)&x_2(t_0) \\ x_1(t_1)&x_2(t_1) \\ x_1(t_2)&x_2(t_2) \\ .&. \\ . & .\\ .& . \end{bmatrix}$
   $x(:,1)=x_1(t), x(:,2)=x_2(t)$
2. 使用Matlab软件求数值解时，高阶微分方程必须等价地变换为一阶微分方程组。

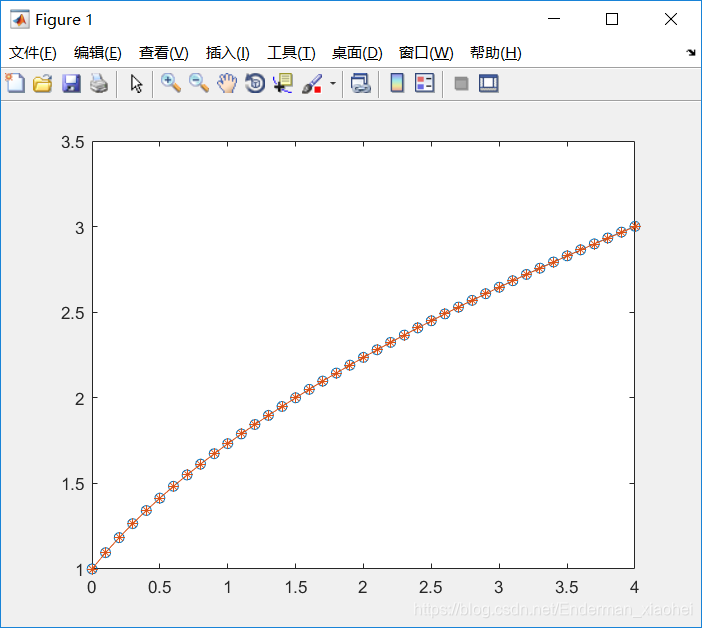
例：求解下述微分方程的解析解和数值解
$y'=y-\frac{2t}{y},y(0)=1,0<t<4$
用Matlab命令阶数值解并画图比较

clear
odefun = @(t,y) y-2*t/y; % 定义局部函数
[t, Y] = ode45(odefun, 0:0.1:4, 1); % 调用Matlab命令
plot(t, Y, 'o-') %画数值解的图
hold on
t1 = 0:0.1:4; y1 = sqrt(1+2*t1); % 画解析解的图
plot(t1, y1, '*-')

点我回顶部 ☚

 
 
 
 
 
 
 
Fin.