这篇文章不涉及数学原理上的说明,用简单的例子说明了EM算法的出彩之处。
001、一个非常简单的例子
假设现在有两枚硬币1和2,,随机抛掷后正面朝上概率分别为P1,P2。为了估计这两个概率,做实验,每次取一枚硬币,连掷5下,记录下结果,如下:
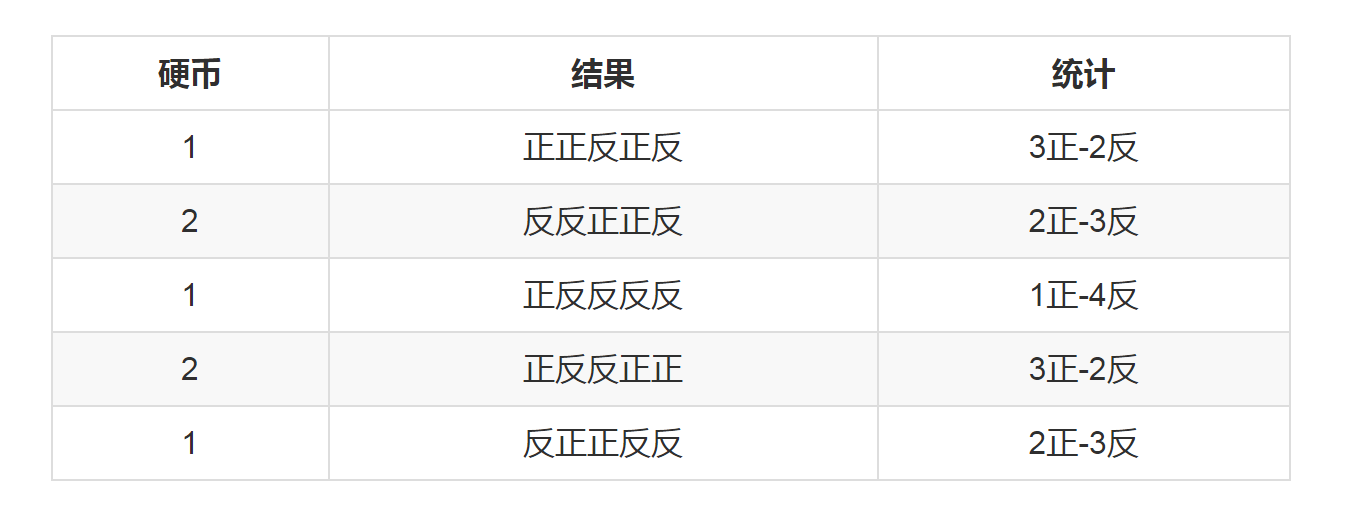
可以很容易地估计出P1和P2,如下:
P1 = (3+1+2)/ 15 = 0.4 P2= (2+3)/10 = 0.5
到这里,一切似乎很美好,下面我们加大难度。
010、加入隐变量z
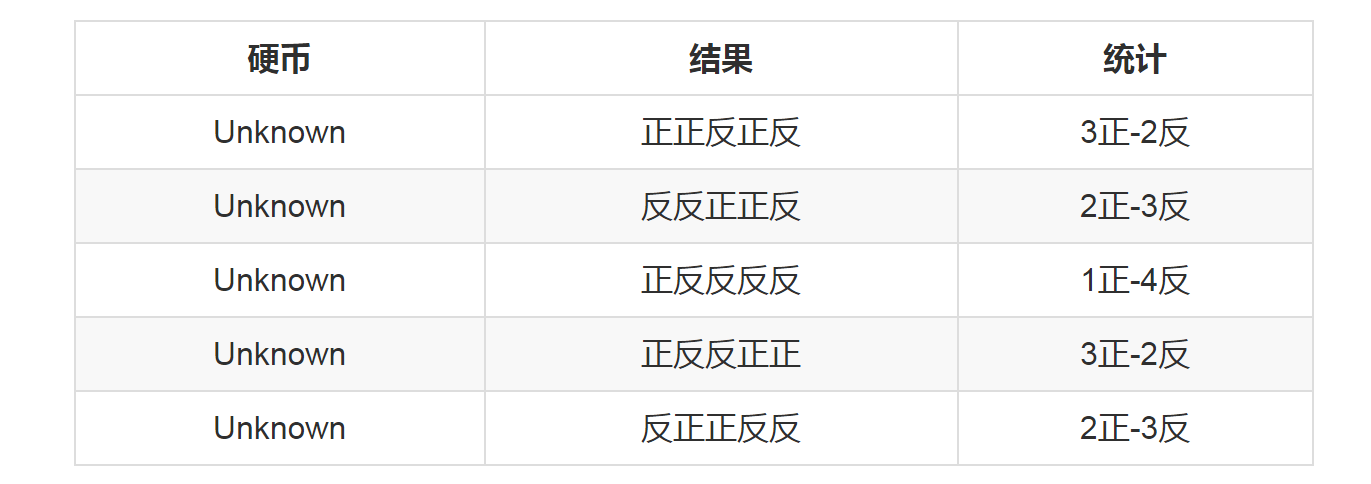
还是上面的问题,现在我们抹去每轮投掷时使用的硬币标记,如下:


好了,现在我们的目标没变,还是估计P1和P2,要怎么做呢? 显然,此时我们多了一个隐变量z,可以把它认为是一个5维的向量(z1,z2,z3,z4,z5),代表每次投掷时所使用的硬币,比如z1,就代表第一轮投掷时使用的硬币是1还是2。但是,这个变量z不知道,就无法去估计P1和P2,所以,我们必须先估计出z,然后才能进一步估计P1和P2。 但要估计z,我们又得知道P1和P2,这样我们才能用最大似然概率法则去估计z,这不是鸡生蛋和蛋生鸡的问题吗,如何破? 答案就是先随机初始化一个P1和P2,用它来估计z,然后基于z,还是按照最大似然概率法则去估计新的P1和P2,如果新的P1和P2和我们初始化的P1和P2一样,请问这说明了什么?(此处思考1分钟)
这说明我们初始化的P1和P2是一个相当靠谱的估计! 就是说,我们初始化的P1和P2,按照最大似然概率就可以估计出z,然后基于z,按照最大似然概率可以反过来估计出P1和P2,当与我们初始化的P1和P2一样时,说明是P1和P2很有可能就是真实的值。这里面包含了两个交互的最大似然估计。 如果新估计出来的P1和P2和我们初始化的值差别很大,怎么办呢?就是继续用新的P1和P2迭代,直至收敛。 这就是下面的EM初级版。
011、EM初级版 我们不妨这样,先随便给P1和P2赋一个值,比如: P1 = 0.2 P2 = 0.7 然后,我们看看第一轮抛掷最可能是哪个硬币。 如果是硬币1,得出3正2反的概率为 0.2*0.2*0.2*0.8*0.8 = 0.00512 如果是硬币2,得出3正2反的概率为0.7*0.7*0.7*0.3*0.3=0.03087 然后依次求出其他4轮中的相应概率。做成表格如下:
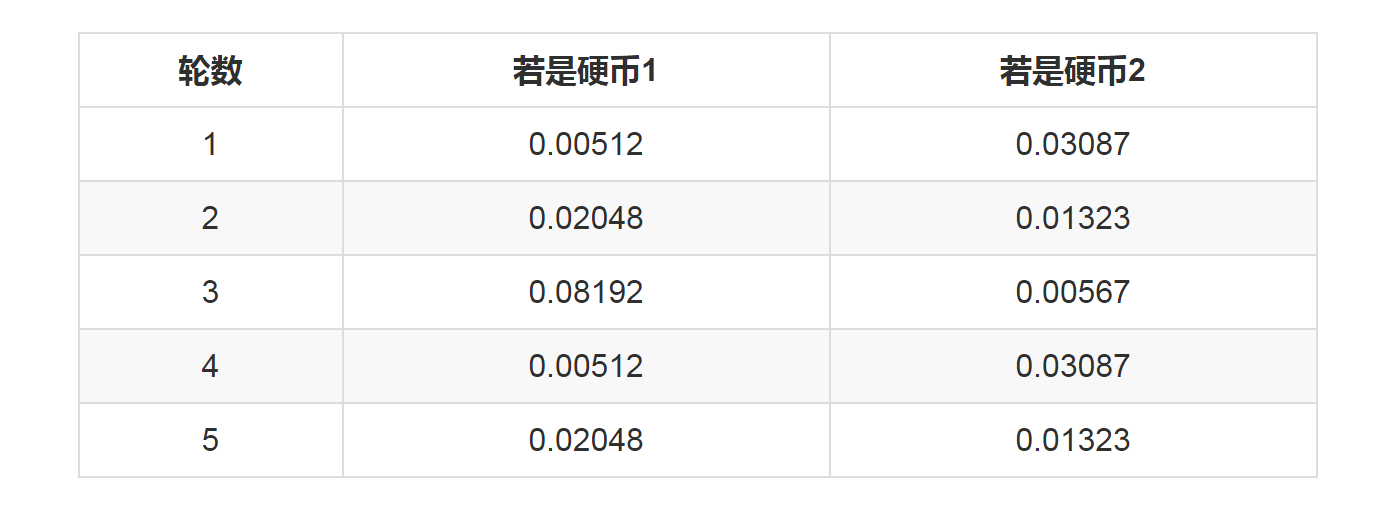
按照最大似然法则: 第1轮中最有可能的是硬币2 第2轮中最有可能的是硬币1 第3轮中最有可能的是硬币1 第4轮中最有可能的是硬币2 第5轮中最有可能的是硬币1 我们就把上面的值作为z的估计值。然后按照最大似然概率法则来估计新的P1和P2。 P1 = (2+1+2)/15 = 0.33 P2=(3+3)/10 = 0.6 设想我们是全知的神,知道每轮抛掷时的硬币就是如本文第001部分标示的那样,那么,P1和P2的最大似然估计就是0.4和0.5(下文中将这两个值称为P1和P2的真实值)。那么对比下我们初始化的P1和P2和新估计出的P1和P2:

看到没?我们估计的P1和P2相比于它们的初始值,更接近它们的真实值了! 可以期待,我们继续按照上面的思路,用估计出的P1和P2再来估计z,再用z来估计新的P1和P2,反复迭代下去,就可以最终得到P1 = 0.4,P2=0.5,此时无论怎样迭代,P1和P2的值都会保持0.4和0.5不变,于是乎,我们就找到了P1和P2的最大似然估计。 这里有两个问题: 1、新估计出的P1和P2一定会更接近真实的P1和P2? 答案是:没错,一定会更接近真实的P1和P2,数学可以证明,但这超出了本文的主题,请参阅其他书籍或文章。 2、迭代一定会收敛到真实的P1和P2吗? 答案是:不一定,取决于P1和P2的初始化值,上面我们之所以能收敛到P1和P2,是因为我们幸运地找到了好的初始化值。
100、EM进阶版 下面,我们思考下,上面的方法还有没有改进的余地? 我们是用最大似然概率法则估计出的z值,然后再用z值按照最大似然概率法则估计新的P1和P2。也就是说,我们使用了一个最可能的z值,而不是所有可能的z值。 如果考虑所有可能的z值,对每一个z值都估计出一个新的P1和P2,将每一个z值概率大小作为权重,将所有新的P1和P2分别加权相加,这样的P1和P2应该会更好一些。 所有的z值有多少个呢?显然,有2^5=32种,需要我们进行32次估值?? 不需要,我们可以用期望来简化运算。
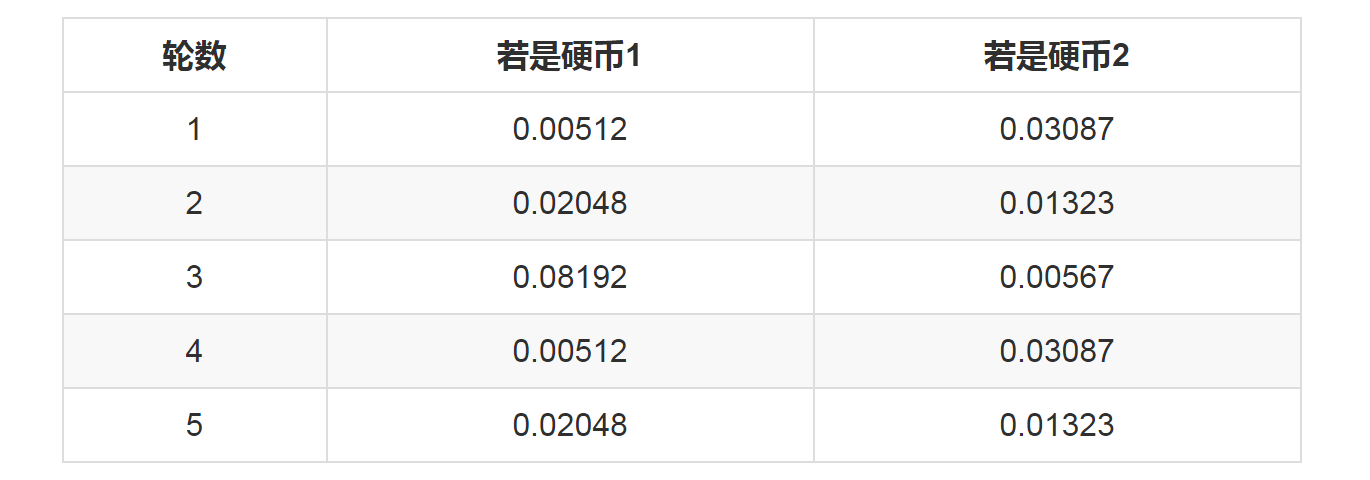
利用上面这个表,我们可以算出每轮抛掷中使用硬币1或者使用硬币2的概率。比如第1轮,使用硬币1的概率是:
0.00512/(0.00512+0.03087)=0.14
使用硬币2的概率是1-0.14=0.86
依次可以算出其他4轮的概率,如下:
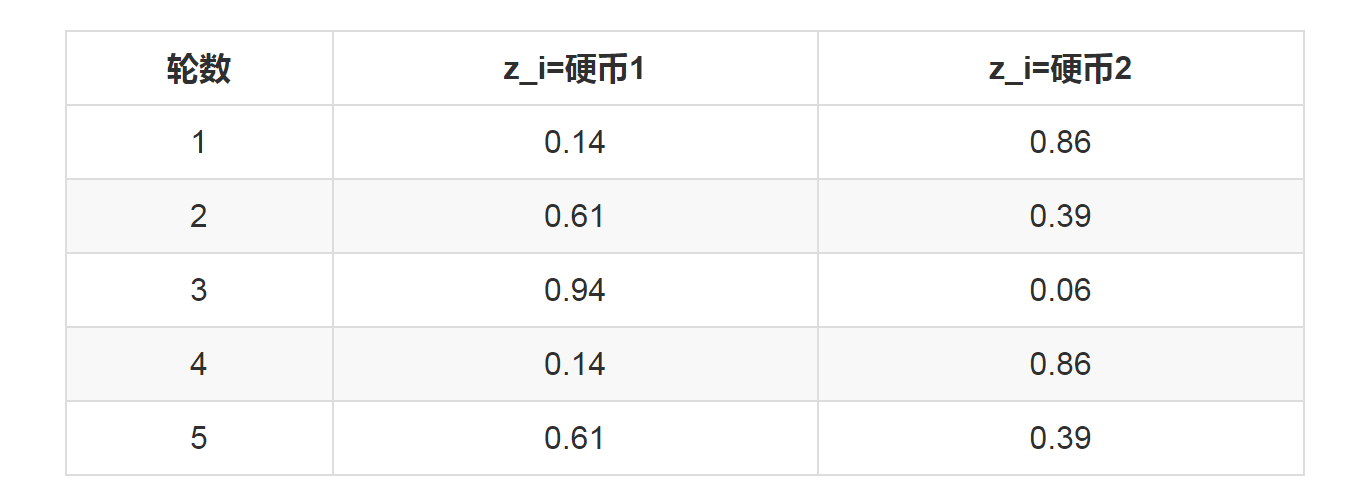
上表中的右两列表示期望值。看第一行,0.86表示,从期望的角度看,这轮抛掷使用硬币2的概率是0.86。相比于前面的方法,我们按照最大似然概率,直接将第1轮估计为用的硬币2,此时的我们更加谨慎,我们只说,有0.14的概率是硬币1,有0.86的概率是硬币2,不再是非此即彼。这样我们在估计P1或者P2时,就可以用上全部的数据,而不是部分的数据,显然这样会更好一些。 这一步,我们实际上是估计出了z的概率分布,这步被称作E步。 结合下表:
我们按照期望最大似然概率的法则来估计新的P1和P2:
以P1估计为例,第1轮的3正2反相当于 0.14*3=0.42正 0.14*2=0.28反
这里有必要对这个进行解释一下,因为我看到这里的时候也有点没转过弯。 P1: 硬币1抛正面的概率,如何求呢? P1 = (用硬币1抛正面的次数)/(用硬币1抛的正反面所有次数)
我们平时认为次数都是整数,但这里引入了概率,所以有了0.14 原来:要么是硬币1,要么是硬币2, 如果第一轮确定用硬币1,则次数正面次数是3,反面是2,则P1的概率为3/(3+2)=0.6 现在:用硬币1的概率是0.14, 所以第一轮用硬币1抛正面的次数是0.14 * 3, 反面是0.14 * 2 现在是对「次数」 乘了 「用硬币1的概率」,0.14仅仅是为了说明在第二轮到第五轮抛掷的时候,使用硬币1的概率是不同的。
但本质上,还是用下面的公式在计算:
P1 = (用硬币1抛正面的次数)/(用硬币1抛的所有次数)
依次算出其他四轮,列表如下:
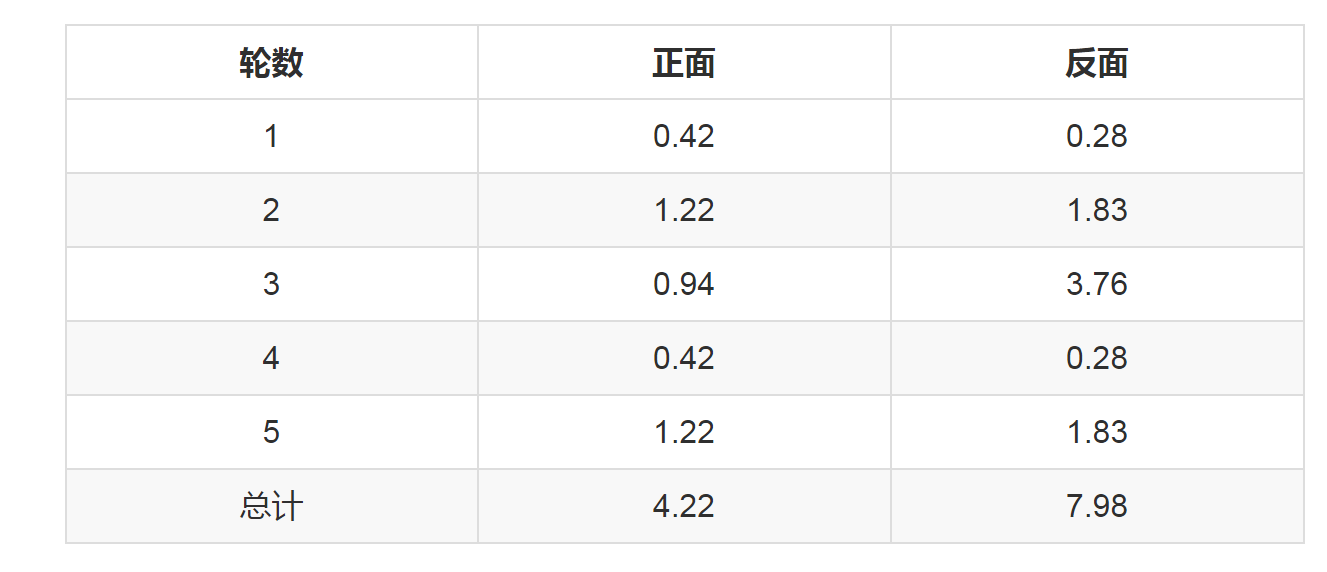
P1=4.22/(4.22+7.98)=0.35
可以看到,改变了z值的估计方法后,新估计出的P1要更加接近0.4。原因就是我们使用了所有抛掷的数据,而不是之前只使用了部分的数据。
这步中,我们根据E步中求出的z的概率分布,依据最大似然概率法则去估计P1和P2,被称作M步。
101、总结
以上,我们用一个实际的小例子,来实际演示了EM算法背后的idea,共性存于个性之中,通过这个例子,我们可以对EM算法究竟在干什么有一个深刻感性的认识,掌握EM算法的思想精髓。
英文文章:What is the expectation maximization algorithm? Chuong B Do & Serafim Batzoglou
原文文章:如何感性地理解EM算法?