Dijkstra算法是由荷兰计算机科学家狄克斯特拉(Dijkstra)于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。
其基本原理是:每次新扩展一个距离最短的点,更新与其相邻的点的距离。当所有边权都为正时,由于不会存在一个距离更短的没扩展过的点,所以这个点的距离永远不会再被改变,因而保证了算法的正确性。不过根据这个原理,用Dijkstra求最短路的图不能有负权边,因为扩展到负权边的时候会产生更短的距离,有可能就破坏了已经更新的点距离不会改变的性质。
举例来说,如果图中的顶点表示城市,而边上的权重表示著城市间开车行经的距离。 Dijkstra算法可以用来找到两个城市之间的最短路径。
图是由节点和连接节点的边构成的。节点之间可以由路径,即边的序列。根据路径,可以从一点到达另一点。在一个复杂的图中,图中两点可以存在许多路径。最短路径讨论了一个非常简单的图论问题,图中从A点到B点 ,那条路径耗费最短? 这个问题又异常复杂,因为网络的构成状况可能很复杂。一个最简单的思路,是找出所有可能的从A到B的路径,再通过比较,来寻找最短路径。然而,这并没有将问题简化多少。因为搜索从A到B的路径,这本身就是很复杂的事情。而我们在搜索所有路径的过程中,有许多路径已经绕了很远,完全没有搜索的必要。比如从上海到纽约的路线,完全没有必要先从上海飞到南极,再从南极飞到纽约,尽管这一路径也是一条可行的路径。
所以,我们需要这样一个算法:它可以搜索路径,并当已知路径包括最短路径时,即停止搜索。我们先以无权网络为例,看一个可行的最短路径算法。
无权网络
无权网络(unweighted network)是相对于加权网络的,这里的“权”是权重。每条边的耗费相同,都为1。路径的总耗费即为路径上边的总数。
我们用“甩鞭子”的方式,来寻找最短路径。鞭子的长度代表路径的距离。
手拿一个特定长度的鞭子,站在A点。甩出鞭子,能打到一些点。比如C和D。
将鞭子的长度增加1。再甩出鞭子。此时,从C或D出发,寻找距离为1的邻接点,即E和F。这些点到A点的距离,为此时鞭子的长度。
记录点E和F,并记录它们的上游节点。比如E(C), F(D)。我们同样可以记录此时该点到A的距离,比如5。
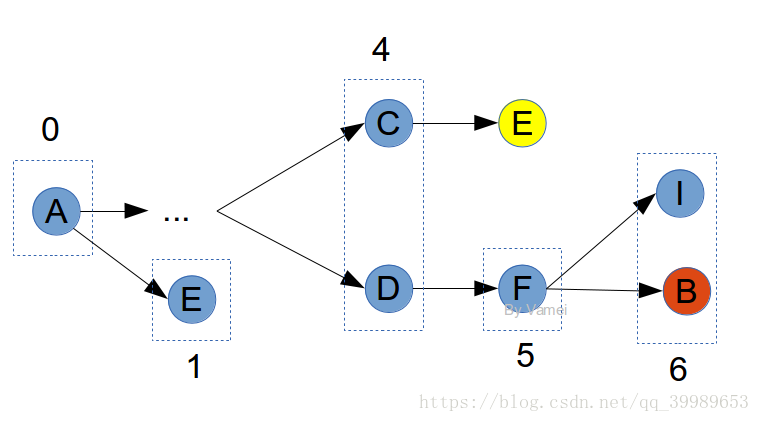
如果要记录节点E时,发现它已经出现在之前的记录中,这说明曾经有更短的距离到E。此时,不将E放入记录中。毕竟,我们感兴趣的是最短路径。如下图中的E:
黄色的E不被记录
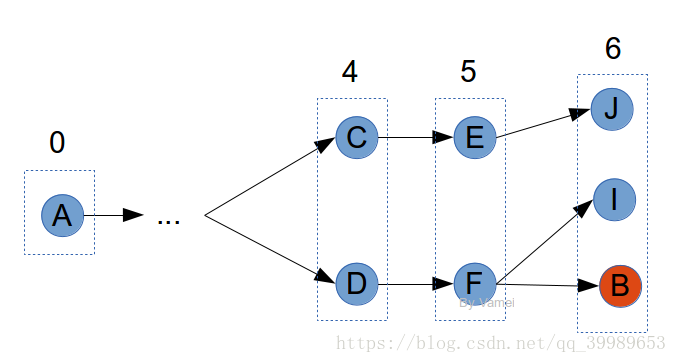
最初的鞭子长度为0,站在A点,只能打到A点自身。当我们不断增加鞭子长度,第一次可以打到B时,那么此时鞭子的长度,就是从A到B的最短距离。循着我们的记录,倒推上游的节点,就可以找出整个最短路径。我们的记录本是个很有意思的东西。某个点放入记录时,此时的距离,都是A点到该点的最短路径。根据记录,我们可以反推出记录中任何一点的最短路径。这就好像真诚对待每个人。这能保证,当你遇到真爱时,你已经是在真诚相待了。实际上,记录将所有节点分割成两个世界:记录内的,已知最短距离的;记录外的,未知的。
加权网络
在加权网络中(weighted network),每条边有各自的权重。当我们选择某个路径时,总耗费为路径上所有边的权重之和。
加权网络在生活中很常见,比如从北京到上海,可以坐火车,也可以坐飞机。但两种选择耗费的时间并不同。再比如,我们打出租车和坐公交车,都可以到市区,但车资也有所不同。在计算机网络中,由于硬件性能不同,连接的传输速度也有所差异。加权网络正适用于以上场景。无权网络是加权网络的一个特例。
这个问题看起来和无权网络颇为类似。但如果套用上面的方法,我们会发现,记录中的节点并不一定是最短距离。我们看下面的例子: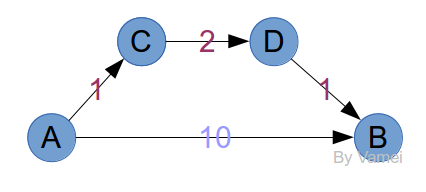
很明显,最短路径是A->C->D->B,因为它的总耗费只有4。按照上面的方法,我们先将A放入记录。从A出发,有B和C两个如果将B和C同时放入记录,那么记录中的B并不符合最短距离的要求。
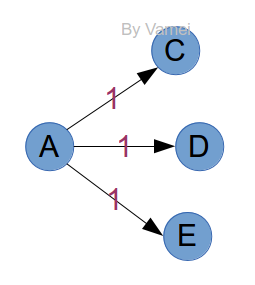
那么,为什么无权网络可行呢?假设某次记录时,鞭子长度为5,那么这次记录点的邻接点,必然是距离为6的点。如果这些邻接点没有出现过,那么6就是它们的最短距离。所有第一次出现的邻接点,都将加入到下次的记录中。比如下面的例子,C/D/E是到达A的邻接点,它们到A的最短距离必然都是1。
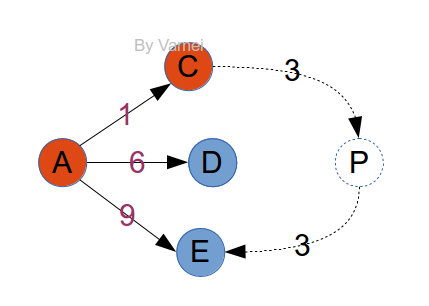
对于加权网络来说,即使知道了邻接点,也无法判断它们是否符合最短距离。在记录C/D/E时,我们无法判断未来是否存在如下图虚线的连接,导致A的邻接点E并不是下一步的最短距离点:
但情况并没有我们想的那么糟糕。仔细观察,我们发现,虽然无法一次判定所有的邻接点为下一步的最短距离点,但我们可以确定点C已经处在从A出发的最短距离状态。A到C的其它可能性,比如途径D和E,必然导致更大的成本。
也就是说,邻接点中,有一个达到了最短距离点,即邻接点中,到达A距离最短的点,比如上面的C。我们可以安全的把C改为已知点。A和C都是已知点,点P成为新的邻接点。P到A得距离为4。
出于上面的观察,我们可以将节点分为三种:
· 已知点:已知到达A最短距离的点。“我是成功人士。”
· 邻接点:有从记录点出发的边,直接相邻的点。“和成功人士接触,也有成功的机会哦。”
· 未知点:“还早得很。”
最初的已知点只有A。已知点的直接下游节点为邻接点。对于邻接点,我们需要独立的记录它们。我们要记录的有:
· 当前情况下,从A点出发到达该邻接点的最短距离。比如对于上面的点D,为6。
· 此最短距离下的上游节点。对于上面的点D来说,为A。
每次,我们将邻接点中最短距离最小的点X转为已知点,并将该点的直接下游节点,改为邻接点。我们需要计算从A出发,经由X,到达这些新增邻接点的距离:新距离 = X最短距离 + QX边的权重。此时有两种情况,
· 如果下游节点Q还不是邻接点,那么直接加入,Q最短距离 = 新距离,Q上游节点为X。
· 如果下游节点Q已经是邻接点,记录在册的上游节点为Y,最短距离为y。如果新距离小于y,那么最小距离改为新距离,上游节点也改为X。否则保持原记录不变。
我们还用上面的图,探索A到E的路径:
第一步
|
状态 |
已知距离 |
上游 |
A |
已知 |
0 |
A |
C |
邻接 |
1 |
A |
D |
邻接 |
6 |
A |
E |
邻接 |
9 |
A |
P |
未知 |
无穷 |
|
第二步
|
状态 |
已知距离 |
上游 |
A |
已知 |
0 |
A |
C |
已知 |
1 |
A |
D |
邻接 |
6 |
A |
E |
邻接 |
9 |
A |
P |
邻接 |
4 |
C |
第二步
|
状态 |
已知距离 |
上游 |
A |
已知 |
0 |
A |
C |
已知 |
1 |
A |
D |
邻接 |
6 |
A |
E |
邻接 |
7 |
P |
P |
已知 |
4 |
C |
第三步
|
状态 |
已知距离 |
上游 |
A |
已知 |
0 |
A |
C |
已知 |
1 |
A |
D |
已知 |
6 |
A |
E |
邻接 |
7 |
P |
P |
已知 |
4 |
C |
最后,E成为已知。倒退,可以知道路径为E, P, C, A。正过来,就是从A到E的最短路径了。
上面的算法是经典的Dijkstra算法。本质上,每个邻接点记录的,是基于已知点的情况下,最好的选择,也就是所谓的“贪婪算法”(greedy algorithm)。当我们贪婪时,我们的决定是临时的,并没有做出最终的决定。转换某个点成为已知点后,我们增加了新的可能性,贪婪再次起作用。根据对比。随后,某个邻接点成为新的“贪无可贪”的点,即经由其它任意邻接点,到达该点都只会造成更高的成本; 经由未知点到达该点更不可能,因为未知点还没有开放,必然需要经过现有的邻接点到达,只会更加绕远。好吧,该点再也没有贪婪的动力,就被扔到“成功人士”里,成为已知点。成功学不断传染,最后感染到目标节点B,我们就找到了B的最短路径。
总结: 这个算法只能计算单元最短路,而且不能计算负权值,这个算法是贪心的思想, dis数组用来储存起始点到其他点的最短路,但开始时却是存的起始点到其他点的初始路程。通过n-1遍的遍历找最短。每次在剩余节点中找dist数组中的值最小的,加入到s数组中,并且把剩余节点的dist数组更新。
程序待续。。。。。。