1. 使用回归进行分类
机器学习中分类是指输入一个样本点,输出这个样本点所属的类别,预测的是一个离散值,如类别(1,2)。
而回归问题是输入一个样本点,预测一个值,这个值是连续值,可以介于\([1,2]\)之间。
以二分类问题为例,我们可不可以通过回归的方法来进行分类呢?比如输入一个样本点,如果是第1类,就让他输出1,如果是第2类就输出-1。通过线性回归的损失函数\(\frac{1}{m}\sum_{i=1}^n(y_i-\hat y)^2\),进行梯度下降,来求参数\(w,b\)最终获得一个超平面进行分类。
这种方法是不行的。因为如下图。
问题:
- 对于左边的图,我们求得是理想的分界线,但是对于右边的图,右下角部分的点属于1类,如果使用绿线的参数来预测右下角点,值会远远大于1,表示分类很正确。但是我们设定损失函数的时候,希望属于第1类的点预测值等于1,因此会使调整参数使右下角的点预测值变小接近1,结果就会使绿线变为紫线,分类不准确
- 对于多分类问题,如类1输出1,类2输出2,类3输出3。回归问题就会假想这三个类别有某种关系,比如类3跟类2比较接近,类2跟类3比较接近,因为输出值离得的比较近。但是实际上没有关系。得不到好结果。

2. 通过概率理解分类问题
我们想,通过求某个样本属于某个类别的概率,在比较属于哪个类别的概率比较大,来判断此样本属于哪个类别。这个想法也叫产生式模型。与之对应的还有判别式模型。两者有什么区别呢。
生成模型:假如有\(C_1,C_2,C_3\)三个类别,求样本\(x\)属于哪个类别。对于产生式模型是,先通过训练集分别求出每个类\(C_1,C_2,C_3\)的联合概率分布。在通过每个联合概率分布求得样本\(x\)属于哪个类别的概率,通过比较属于哪个类别概率大来判断类别。
如朴素贝叶斯模型
判定模型:通过一系列的训练集样本,直接生成一个决策边界,给定一个样本,可以直接带入函数中求得属于哪一类。即处在决策边界的哪一方。
如逻辑回归,支持向量机
下图展示了判定模型跟生成模型:可以看出判定模型是求出了决策边界,生成模型是求得联合概率分布
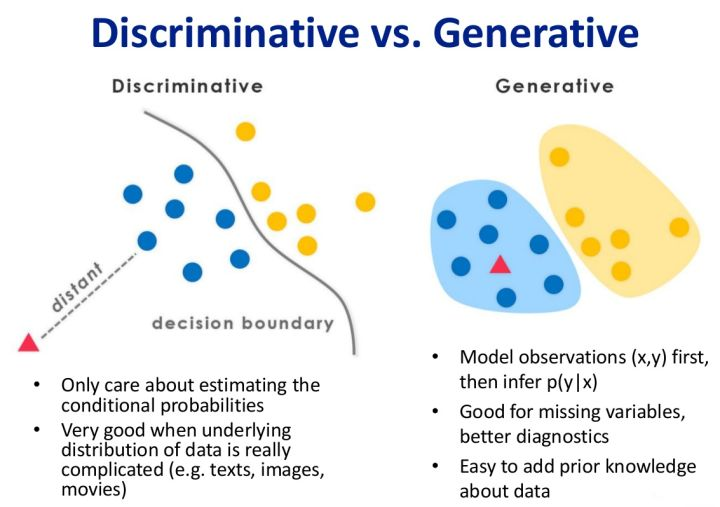
优缺点:
- 生成模型需要的样本数量少,因为只需进行统计技术来获得模型。
- 生成模型准确率一般不高,因为需要人为指定属于哪一种分布。
- 生成模型对噪声有更好的鲁棒性
- 判定模型准确率高,可直接学习求得参数,简化学习。
假设分布符合高斯分布,则给定训练集,对每一类的数据集我们可以求得一个分布函数,其中\(\mu\)为此类所有样本的平均值,\(\Sigma\)为此类样本维度对应的协方差矩阵。
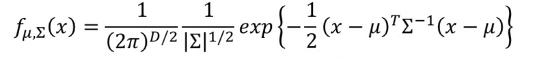
有了分布函数,给定一个样本\(x\)我们就可以求得此样本在此类分布中出现的可能行。对于某类的高斯分布函数,属于这一类的样本点的概率和是最大的。即
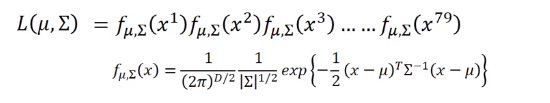
但平时我们不会为每个类别建立一个高斯分布函数,而是共用一个协方差,即求这样一个高斯分布函数,使函数值最大,其中\(\mu_1,u_2\)是训练集中每个类的样本的平均值,\(\Sigma\) 等于每个类对应的比例的协方差之和,即假如有79个1类样本,61个类样本,一共140个样本,\(\Sigma=\frac{79}{140}\Sigma_1+\frac{61}{140}\Sigma_2\)
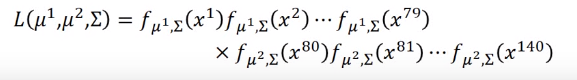
若所有样本的每一个维度都相互独立,\(x_1,x_2 \cdots x_k\)为\(x\)的每一个维度,那我们可以令:
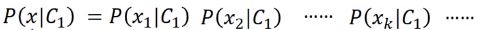
但实际中,每个属性不是相互独立的,这个模型类效果不会很好。
下面看sigmoid函数跟后验概率的联系。

可以看到若将\(ln\frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)}\)带入sigmoid中得到的就是样本\(x\)属于类1的概率,在将z进行化简,\(C_1,C_2\)共用协方差得到
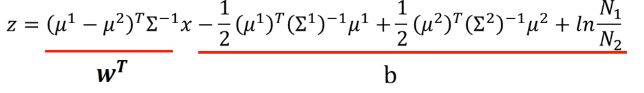
即我们可以简化为求解向量\(w^T\)跟常数\(b\)来求解样本\(x\)所属的类1的概率。
3. 逻辑回归
有了sigmoid函数后我们看如何来建立逻辑回归模型解决分类问题。
我们的假设函数为\(f_{w,b}(x)=\sigma(\sum_i w_i x_i+b)\)带入样本\(x\)输出值\((0,1)\)的预测值,\(\sigma\)为sigmoid函数。那我们的损失函数为应该设为什么样子。首先想到的是求平方差的方法,即设
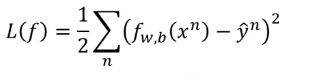
在通过梯度下降的方式求得参数\(w,b\) ,直觉上行的通,但是通过下图我们可以看出,通过求平方差设定的损失函数的图是红色网格。在整个样本空间中每个点的梯度值都很小,参数很难更新,因此我们得寻找其他方法。
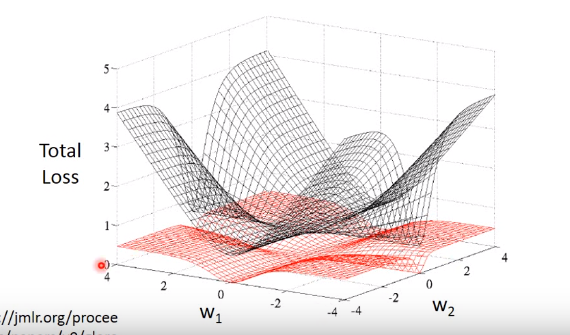
设函数为下面公式,其中\(x^1,x^2 \cdots x^N为样本点\),\(x^1,x^2,x^N\)为类1,\(x^3\)为类2

我们要求得的参数$w^,b^ $就是使函数最大的值。对函数L做如下转化
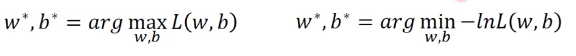
设第一类的标签为1,第二类的标签为0,可以得到如下式子,这其实使伯努利的交叉熵形式。
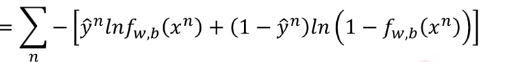
下面简要介绍交叉熵
先说信息量,信息量的公式为\(-log_2p\),\(p\)为某个时间事件发生的概率。通过公式我们可以看到,信息量与概率呈反比。这其实有很直观的解释,如果我们对某件事很确定,那这件事带给我们的信息量就很少,如果对某件事一点把握都没有,那他的信息量就很大。
信息熵:信息熵是信息量的期望公式如下,因此信息熵是平均而言发生一个事件我们得到的信息量的大小。熵越大不确定就越大,熵越小不确定性就越小。

对于每个系统,它都有个真实分布记,通过这个真实分布我们可以通过信息熵的公式求出这个系统的不确定性大小。
交叉熵:其用来衡量\(p\)的分布与\(q\)的分布有多接近
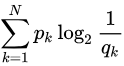
\(p_k\)为真实分布的概率,即训练集中标签,\(q_k\)为我们模拟的分布函数求得的概率,交叉熵的值越小,\(q_k\)的值越接近$q _k $,即我们模拟的函数越接近真实分布,预测越准确。因此我们在机器学习分类算法中,我们会最小化交叉熵,交叉熵越小,我们的预测就越准确。回到我们定义的损失函数,我们最小化我们的损失函数,就可以使我们的预测值,接近标签值。
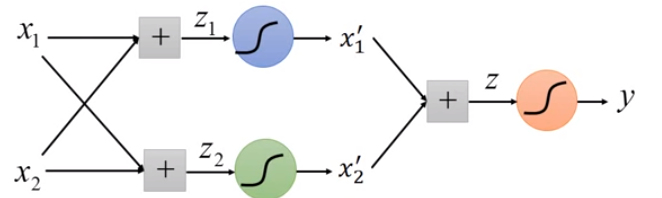
逻辑回归的一个局限性是只能产生线性分界线,可以通过进行特征转化,来将之前非线性可分的数据转换为线性可分。还可以通过组合多个逻辑回归来产生非线性分界线。其实就是神经网络。
4. 参考
- 李宏毅机器学习
- 信息熵是什么? - 滴水的回答 - 知乎
https://www.zhihu.com/question/22178202/answer/49929786 - 如何通俗的解释交叉熵与相对熵? - Noriko Oshima的回答 - 知乎
https://www.zhihu.com/question/41252833/answer/108777563