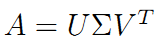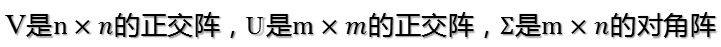1. 最小二乘问题的优化理论

1. 1 问题描述

最小二乘问题是找到最符合实际测量值的观测模型，使得模型和测量值之间的误差最小化：
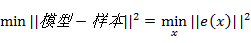
在这里插入图片描述
其中e(x)为模型和样本之间的误差，在SLAM中亦可以看作为观测值和估计值之间的误差。通过求解该问题我们就能够优化我们的模型函数使之更接近与真实的函数模型

1.2 求解思路

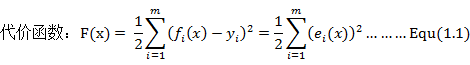
在这里插入图片描述
假如该问题为线性的我们可以直接对目标函数求导，并且令其等于零，以此求得其极值，并通过比较求取全局最小值(Global Minimizer)，并将其最为目标函数的解。
但是如果问题为非线性，由于函数复杂，此时我们通常无法直接写出其导数形式，因此我们不再去试图直接找到全局最小值，而是退而求其次通过不停的迭代计算寻找最好的增量 ${\Delta}x$ ,使得代价函数不断减小直到不能减小为止。

1.3寻找增量的方法

1.一阶梯度法
类似神经网络的反向传播算法（BP），我们参考公式1.2对函数进行一阶泰勒展开：
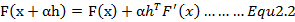
在这里插入图片描述
此处我们将公式1.1中的 ${\Delta}x$ 拆解为迭代方向 $h^T$ 和步长 $\alpha$
函数的下降方向（增量迭代方向）将永远为函数的负梯度方向。该结论亦可通过下面两张图进行直观的说明:

当迭代点在极小值左侧时，梯度（近似倒数）为负数，增量迭代方向为正数;当迭代点在极小值右侧时，梯度（近似倒数）为正数，增量迭代方向为负数
2.二阶梯度法
但是由于该算法过于贪婪，只考虑一阶梯度，步长确定困难，存在优化非线性问题难以收敛的问题，一般不考虑此种方法。
牛顿法，也叫二阶梯度法解决了一阶梯度法难以收敛的问题，我们参考公式1.2对函数进行二阶泰勒展开：
$F(x+{\Delta}x)=F(x)+J(x){\Delta}x+1/2{\Delta}x^TH(x){\Delta}x.... ...Equ2.3$
式中，J(x)为雅克比矩阵（多元函数的偏微分矩阵），也就是是F(x)关于x的导数；而H就是二阶倒数，也被称为海赛矩阵。
对式2.3求解增量，也就是对等式右侧求关于 ${\Delta}x$ 的导数，并另之等于0，求得：
$H{\Delta}x=-J^T$
但是海赛矩阵求解繁琐，一般用GN法近似求解。
3. 高斯牛顿法（GN）
高斯牛顿法是一种求解非线性最小二乘的简单算法，该算法的基本思想是将函数非线性F(x)进行一阶泰勒展开（此处我们展开的只是函数e(x)而非代价函数F(x)）：
$e(x+{\Delta}x)=e(x)+J(x){\Delta}x.... ...Equ2.4$
代入代价函数得到：
$1/2(e(x+{\Delta}x))^2 =1/2(\parallel$ e(x) $\parallel$ ^2+ $2e(x)^2$ J(x) ${\Delta}x+{\Delta}x^TJ(x)^TJ(x){\Delta}x).... ...Equ2.4$
对式2.4右侧求关于 ${\Delta}x$ 的导数，并另之等于0，求得：
$J(x)^TJ(x)$ ${\Delta}$ x= $-J(x)^T$ e(x),
另之为H(x) ${\Delta}$ x=g…Euq4.9为增量方程
求解步骤：
在这里插入图片描述
4. 列文伯格.马夸尔特法（LM）
由于式中的 $J(x)^TJ(x)$ 只是近似二阶海赛矩阵，只有半正定性，不一定有逆矩阵，所以有了LM法对GN进行优化
LM算法是基于信赖区域理论(Trust Region Method)进行计算的。这是因为高斯牛顿法中的泰勒展开只有在展开点附近才会有比较好的效果，因此为了确保近似的准确性我们需要设定一个具有一定半径的区域作为信赖区域。
采用信赖区域法我们就需要明确该区域该怎么确定。在LM算法中信赖区大小的确定也是运用增益比例来进行判定的：
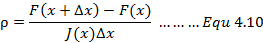
在这里插入图片描述
基于信赖区域我们能够重新构建一个更有效的优化框架：

引入拉格朗日乘子将该有约束优化问题转化为无约束优化问题后我们能够得到：

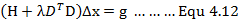
简化形式，D=I（单位矩阵），又有最终的LM增量方程：

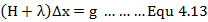
2. 利用Eign对线性方程求解

得到增量方程之后，通常可以通过正规方程、QR 分解、乔姆斯基分解(Cholesky decomposition)和奇异值分解(SVD)等方法求解。

2.1 正规方程

判定线性方程组有解且唯一的定理为克拉默法则，具体为：线性方程组 Ax = b 的系数矩阵 A（nxn）的行列式 d =| A | 不等于0 ,那么 x 是有解且唯一的
若A不是方阵,将通过正规方程求其广义逆矩阵:
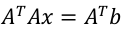
在这里插入图片描述
求解:

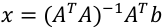
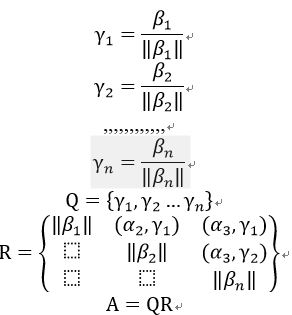
2.2 QR 分解

QR 分解原理是 Gram–Schmidt 正交化方法

令:
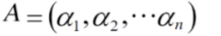
在这里插入图片描述
Gram–Schmidt 正交化:

3.3 乔姆斯基分解（Cholesky）

若A为实对称正定矩阵:
对称矩阵A对任意非零向量x，满足x’Ax>0，则定义A正定。
然后对称矩阵是实矩阵的时候，满足上边定义我们叫他“正定矩阵”
矩阵分解步骤:
在这里插入图片描述

3.4 奇异值分解(SVD)

SVD不仅是一个数学问题，在工程应用中的很多地方都有它的身影，用SVD可以很容易得到任意矩阵的满秩分解，用满秩分解可以对数据做压缩。可以用SVD来证明对任意M*N的矩阵均存在如下分解：
在这里插入图片描述
简单介绍:

3.5 Eigen编程实践

在这里插入图片描述
测试代码如下：

//AUTHOR:JIANGCHENG
//求解线性方程问题
#include <iostream>
#include <ctime>
using namespace std;

#include <Eigen/Core>
#include <Eigen/Dense>
#define MATRIX_SIZE 100

int main(){
    Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic> matrix_NN;
    Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic> v_Nd;
    matrix_NN = Eigen::MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
    v_Nd=Eigen::MatrixXd::Random(MATRIX_SIZE, 1);
//    cout<<"100x100的矩阵A为:\n"<<matrix_NN<<endl;
    cout<<"b向量为：\n"<<v_Nd<<endl;
// 对随机矩阵v_Nd处理，生成实对称正定矩阵A_sym
    Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic> matrix_NN_sym;
    matrix_NN_sym = matrix_NN;
    for (int i=0; i<MATRIX_SIZE; i++){
        for (int j=0; j<MATRIX_SIZE; j++){
            if(i>j){

                matrix_NN_sym(i,j)=matrix_NN_sym(j,i);
            }
        }
    }
//    cout<<"100x100的正定矩阵A_sym为:\n"<<matrix_NN_sym<<endl;

//直接用逆求解
    clock_t time_stt = clock();
    Eigen::Matrix<double,MATRIX_SIZE,1> x_inverse = matrix_NN_sym.inverse()*v_Nd;
    cout<<"直接求逆，耗时:\n"<<(clock()-time_stt)/(double)
           CLOCKS_PER_SEC<<"ms"<<endl;
//QR求解
    clock_t time_stt1 = clock();
    Eigen::Matrix<double,MATRIX_SIZE,1> x_QR = matrix_NN_sym.colPivHouseholderQr().solve(v_Nd);
    cout<<"QR分解，耗时:\n"<<(clock()-time_stt1)/(double)
           CLOCKS_PER_SEC<<"ms"<<endl;
//LDL^T Cholesky求解
    clock_t time_stt2 = clock();
    Eigen::Matrix<double,MATRIX_SIZE,1> x_Cholesky_ldlt = matrix_NN_sym.ldlt().solve(v_Nd);
    cout<<"LDL^T分解，耗时:\n"<<(clock()-time_stt2)/(double)
           CLOCKS_PER_SEC<<"ms"<<endl;
//SVD分解
    clock_t time_stt3 = clock();
    Eigen::Matrix<double,MATRIX_SIZE,1> x_bdc_svd =matrix_NN_sym.bdcSvd(Eigen::ComputeFullU|Eigen::ComputeFullV).solve(v_Nd);
    cout<<"SVD分解，耗时:\n"<<(clock()-time_stt3)/(double)
           CLOCKS_PER_SEC<<"ms"<<endl;
    return 0;
}

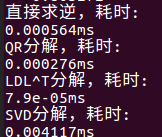
分别用时:
在这里插入图片描述

扫描二维码关注公众号，回复： 5680440 查看本文章

视觉slam14讲学习（三）之非线性最小二乘理论