积分之自适应辛普森法 [学习笔记]

版权声明：https://blog.csdn.net/huashuimu2003 https://blog.csdn.net/huashuimu2003/article/details/86772247

声明

本文证明和积分知识普及基本来自xyz32768。

一.预备技能

积分

积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种。直观地说，对于一个给定的正实值函数，在一个实数区间上的定积分可以理解为在坐标平面上，由曲线、直线以及轴围成的曲边梯形的面积值（一种确定的实数值）。
积分的一个严格的数学定义由波恩哈德·黎曼给出（参见条目“黎曼积分”）。黎曼的定义运用了极限的概念，把曲边梯形设想为一系列矩形组合的极限。从十九世纪起，更高级的积分定义逐渐出现，有了对各种积分域上的各种类型的函数的积分。比如说，路径积分是多元函数的积分，积分的区间不再是一条线段（区间[a,b]），而是一条平面上或空间中的曲线段；在面积积分中，曲线被三维空间中的一个曲面代替。对微分形式的积分是微分几何中的基本概念。——摘自某度

其实，没那么麻烦，这样解释，可能更容易懂些（就是加颜色的话）：
积分（integral）的几何意义是函数的曲线上 $x$ 的一段区间与 $x$ 轴围成的曲边梯形的面积：

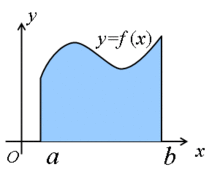
$x$ 的区间为 $[a,b]$
公式： $\int ^{b}_{a}f\left( x\right) dx$

计算方法一：分割成无穷多个小区间。
$\int ^{b}_{a}f\left( x\right) dx=\lim _{x\rightarrow \infty }\sum ^{n}_{i=1}\dfrac {b-a}{n}f\left(a +\dfrac {b-a}{n}i\right)$

计算方法二：牛顿-莱布尼茨公式。
定义:
如果函数 $f(x)$在区间 $[a,b]$上连续，并且存在原函数 $F(x)$ ，
则
$\int ^{b}_{a}f\left( x\right) dx=F(b)-F(a)=F\left( x\right) | ^{b}_{a}$

如果容易求出 $n$ 趋近于无穷大时 $f$ 的和，可以使用方法一，如 $f(x)=x^{2}$。
而这时 $f(x)=\dfrac {1}{x}$就不适用。
如果容易求得 $F$ ，可以使用方法二，如 $f(x)=\dfrac {1}{x}$ 。
但如果两个特点都不满足，那么两种方法都无法使用。
于是，我们引入了数值积分。
最常用的就是自适应辛普森积分。

二.辛普森公式

借用一下大佬xyz32768的证明：
$\int ^{b}_{a}f\left( x\right) dx\approx\int ^{b}_{a}\left( Ax^{2}+Bx+C\right) dx$
$=\frac{A}{3}(b^3-a^3)+\frac{B}{2}(b^2-a^2)+C(a-b)$
$=\frac{(b-a)}{6}(2A(b^2+ab+a^2)+3B(b+a)+6C)$
$=\frac{(b-a)}{6}(2Ab^2+2Aab+2Aa^2+3Bb+3Ba+6C)$
$=\frac{(b-a)}{6}(Aa^2+Ba+C+Ab^2+Bb+C+4A(\frac{a+b}{2})^2+4B(\frac{a+b}{2})+4C)$
$=\frac{(b-a)}{6}(f(a)+f(b)+4f(\frac{a+b}{2}))$
我们得到辛普森公式：
$\int ^{b}_{a}f\left( x\right) dx\approx \dfrac {\left( b-a\right) \left( f\left( a\right) +f\left( b\right) +4f\left( \dfrac {a+b}{2}\right) \right) }{6}$
b−a 的值越小，上式两边越接近。

三.处理精度问题

同样来自上面的大佬。

有了 $Simpson$ 公式，一个自然的想法是把积分区间拆成多个小区间后求和。
但是分成区间的个数和长度因积分区间和精度要求甚至被积函数而异。
换句话说，分的区间数太少不满足精度要求，太多了会 TLE 。
「自适应」就是求积分时能够自动控制切割的区间大小和长度，使精度能满足要求。
具体地： $solve(l,r,f)$表示求 $\int ^{r}_{l}f(x)dx$。
（1）取 $mid=\dfrac {l+r}{2}$。
（2）用 $Simpson$ 公式近似计算 $f(x)$ 在区间 $[l,mid]$和区间 $[mid,r]$内的积分，分别为 $ls$ 和 $rs$ ，及 $[l,r]$的近似积分 $sum$ 。
（3）如果 $ls+rs$ 与 $sum$的误差允许，则返回 $sum$ 。
（4）否则递归 $solve(l,mid)$和 $solve(mid,r)$，返回这两个递归计算结果的和。

四.例题

P4525 【模板】自适应辛普森法1

title

LUOGU 4525

题目描述
计算积分
$\int ^{R}_{L}\dfrac {cx+d}{ax+b}dx$
结果保留至小数点后6位。
数据保证计算过程中分母不为0且积分能够收敛。
输入输出格式
输入格式：
一行，包含6个实数a,b,c,d,L,R
输出格式：
一行，积分值，保留至小数点后6位。
输入输出样例
输入样例#1：
1 2 3 4 5 6
输出样例#1：
2.732937
说明
a,b,c,d∈[-10,10]
-100≤L<R≤100 且 R-L≥1

analysis

嗯，感觉是在套板子写。

code

#include<bits/stdc++.h>
const double eps=1e-12;
static double a,b,c,d;

inline double F(double x)
{
    return (c*x+d)/(a*x+b);
}

inline double Simpson(double l,double r)
{
    return (r-l)*(F(l)+4.0*F((l+r)/2.0)+F(r))/6.0;
}

inline double Adaptive(double l,double r,double ans)
{
    double mid=(l+r)/2.0,left=Simpson(l,mid),right=Simpson(mid,r);
    if (fabs(left+right-ans)<eps)
        return left+right;
    else
        return Adaptive(l,mid,left)+Adaptive(mid,r,right);
}

int main()
{
    static double L,R;
    scanf("%lf %lf %lf %lf %lf %lf",&a,&b,&c,&d,&L,&R);
    printf("%.6lf",Adaptive(L,R,Simpson(L,R)));
    return 0;
}

P4526 【模板】自适应辛普森法2

title

LUOGU 4526

题目描述
计算积分
$\int ^{\infty }_{0}x^{\dfrac {a}{x}-x}dx$
保留至小数点后5位。若积分发散，请输出"orz"。
输入输出格式
输入格式：
一行，包含一个实数，为a的值
输出格式：
一行，积分值或orz
输入输出样例
输入样例#1：
2.33
输出样例#1：
1.51068
说明
a<=50
请注意时空限制。

analysis

这道同样是套板子，不过不要被式子的无穷大吓到了。将函数图像画出来，可以轻易地发现，当大于一定值时，函数趋于 $0$，对答案基本没有贡献。这个值随着 $a$增大增大，然而当 $a=50$时，这个值不超过 $8$，为了求稳就可以从 $eps$积分到 $20$。为什么不从 $0$开始?因为当 $a=0$时， $f(0)=1$而不是 $0$，所以计算会出现错误。避免特殊点对积分产生影响也是辛普森自适应积分的一个重点。记得 $eps$开小一点，最好开小 $4$个数量级。

什么时候无解?画一下图可以发现，当 $a&lt;0$时， $\lim\limits_{x\to 0} f(x)\to+\infty$，函数不收敛。直接判掉即可。——Great_Influence

code

#include<bits/stdc++.h>
using namespace std;
const double eps=1e-9;
static double a;

inline double F(double x)
{
    return pow(x,(a/x)-x);
}//原函数

inline double Simpson(double l,double r)
{
    return (r-l)*(F(l)+4.0*F((l+r)/2.0)+F(r))/6.0;
}//三点辛普森法

inline double Adaptive(double l,double r,double ans)
{
    double mid=(l+r)/2.0,left=Simpson(l,mid),right=Simpson(mid,r);
    if (fabs(left+right-ans)<=eps)
    	return ans;
    else
    	return Adaptive(l,mid,left)+Adaptive(mid,r,right);
}//自适应辛普森法

int main()
{
    scanf("%lf",&a);
    if (a<0)
        return puts("orz"),0;//判断收敛/发散
    printf("%.5lf",Adaptive(eps,20,Simpson(eps,20)));
    return 0;
}

summary

代码真心不长，证明略有难度，不过记住结论就行了，然后，很重要的是，告诉我们，积分并不难（除了不定积分，这玩意儿我到现在都不知道是啥，只知道有个这东西）。