学习权重

你了解了如何使用感知器来构建 AND 和 XOR 运算，但它们的权重都是人为设定的。如果你要进行一个运算，例如预测大学录取结果，但你不知道正确的权重是什么，该怎么办？你要从样本中学习权重，然后用这些权重来做预测。

要了解我们将如何找到这些权重，可以从我们的目标开始考虑。我们想让网络做出的预测与真实值尽可能接近。为了能够衡量，我们需要有一个指标来了解预测有多差，也就是误差 (error)。一个普遍的指标是误差平方和 sum of the squared errors (SSE)：

$\frac{1}{2}\sum_\mu \sum_j \left[ y^{\mu}_j - \hat{y} ^{\mu} _j \right]^2E=21∑μ∑j[yjμ−y^jμ]2$

这里 $\hat yy^ 是预测值 yy 是真实值。一个是所有输出单元 jj 的和，另一个是所有数据点 \muμ 的和。这里看上去很复杂，但你一旦理解了这些符号之后，你就能明白这是怎么回事了。$

首先是内部这个对 $\hat yy^ 与真实值 yy 之间的差的平方，再求和。$

另一个对 $\muμ 的求和是针对所有的数据点。也就是说，对每一个数据点，计算其对应输出单元的方差和，然后把每个数据点的方差和加在一起。这就是你整个输出的总误差。$

SSE 是一个很好的选择有几个原因：误差的平方总是正的，对大误差的惩罚大于小误差。同时，它对数学运算也更友好。

回想神经网络的输出，也就是预测值，取决于权重

$\hat{y}^{\mu}_j = f \left( \sum_i{ w_{ij} x^{\mu}_i }\right)y^jμ=f(∑iwijxiμ)$

相应的，误差也取决于权重

$\frac{1}{2}\sum_\mu \sum_j \left[ y^{\mu}_j - f \left( \sum_i{ w_{ij} x^{\mu}_i }\right) \right]^2E=21∑μ∑j[yjμ−f(∑iwijxiμ)]2$

我们想让网络预测的误差尽可能小，权重是让我们能够实现这个目标的调节旋钮。我们的目的是寻找权重 $w_{ij}wij 使得误差平方 EE 最小。通常来说神经网络通过梯度下降来实现这一点。$

梯度下降

如 Luis 所说，用梯度下降，我们通过多个小步骤来实现目标。在这个例子中，我们希望一步一步改变权重来减小误差。借用前面的比喻，误差就像是山，我们希望走到山下。下山最快的路应该是最陡峭的那个方向，因此我们也应该寻找能够使误差最小化的方向。我们可以通过计算误差平方的梯度来找到这个方向。

梯度是改变率或者斜度的另一个称呼。如果你需要回顾这个概念，可以看下可汗学院对这个问题的讲解。

要计算变化率，我们要转向微积分，具体来说是导数。一个函数 $x^2x2 ，x^2x2 的导数是 f'(x) = 2xf′(x)=2x。所以，在 x = 2x=2 这个点斜率 f'(2) = 4f′(2)=4。画出图来就是：$

梯度示例

梯度就是对多变量函数导数的泛化。我们可以用微积分来寻找误差函数中任意一点的梯度，它与输入权重有关，下一节你可以看到如何推导梯度下降的步骤。

下面我画了一个拥有两个输入的神经网络误差示例，相应的，它有两个权重。你可以将其看成一个地形图，同一条线代表相同的误差，较深的线对应较大的误差。

每一步，你计算误差和梯度，然后用它们来决定如何改变权重。重复这个过程直到你最终找到接近误差函数最小值的权重，即中间的黑点。

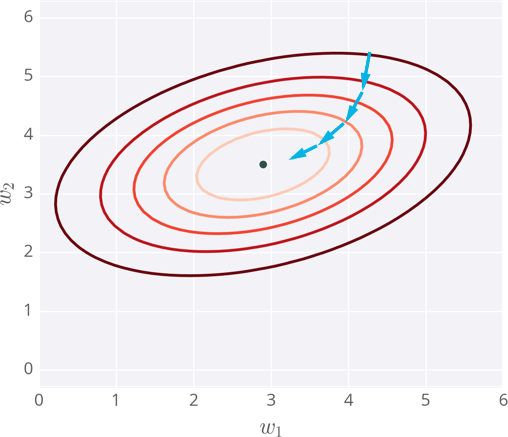
Gradient descent steps to the lowest error

因为权重会走向梯度带它去的位置，它们有可能停留在误差小，但不是最小的地方。这个点被称作局部最低点。如果权重初始值有错，梯度下降可能会使得权重陷入局部最优，例如下图所示。

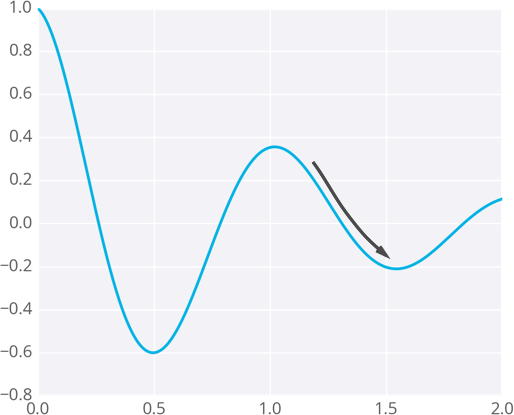
梯度下降引向局部最低点

有方法可以避免这一点，被称作 momentum.