[tensorflow应用之路]什么是深度神经网络——通过实现简单的神经网络理解DNN

在之前的文章中，我们学习了如何使用tensorflow保存和载入一个深度神经网络，如果是抄别人的网络然后用一下，这些知识肯定足够了。但对于学习tensorflow的大多数算法工程师们来说，不自己实现一个深度网络肯定是浑身难受。本章将介绍深度神经网络中最基本的四个概念：
- 前向预测(forward propagation)
- 激活和损失函数(activation function & loss function)
- 反向传播(backward propagation)
- 梯度优化(gradient optimizer)
围绕以上四点，我们使用tensorflow（你也可以使用numpy作为练习）自己动手实现一个麻雀网络（麻雀虽小五脏俱全之意）。如果你认真看完本章，将会对深度神经网络有一个全面的了解。

1.前向预测

传统的人工神经网络（ANN）由三部分组成：输入层，隐藏层，输出层，这三部分各占一层。而深度神经网络的“深度”二字表示它的隐藏层大于2层，这使它有了更深的抽象和降维能力。具体的区别可以参考这篇文章：What is the difference between a neural network and a deep neural network?
在下图中，我们模拟了一个最最简单的深度神经网络。
这里写图片描述
其中，i表示输入层（最左），h1和h2表示隐藏层（中间两个），o表示输出层（最右）。z1和z2表示激活函数处理后的结果，如果你现在不理解，可以先忽略这两个数，稍后再说。
前向预测部分如下：

h_{1} = w_{1} * i + b_{1} z_{1} = σ (h_{1}) h_{2} = w_{2} * z_{1} + b_{2} z_{2} = σ (h_{2}) o = w_{3} * z_{2} + b_{3}

$h_{1}=w_{1}*i+b_{1}\\z_{1}=\sigma (h_{1})\\ h_{2}=w_{2}*z_{1}+b_{2}\\z_{2}=\sigma (h_{2})\\ o=w_{3}*z_{2}+b_{3}$
一般的，w称为权重（weight），b称为偏置（bias）,这两个为需要求解的值。

σ

$\sigma$ 称为激活函数。
使用tensorflow实现它：

import tensorflow as tf

inputs=tf.placeholder(tf.float32,(10,1))
labels=tf.placeholder(tf.float32,(1,1))

w1 = tf.Variable(tf.random_uniform((7, 10,),0.0,1.0))
b1 = tf.Variable(tf.random_uniform((7, 1,),.0,1.0))
w2 = tf.Variable(tf.random_uniform((3, 7,),.0,1.0))
b2 = tf.Variable(tf.random_uniform((3, 1,),.0,1.0))
w3 = tf.Variable(tf.random_uniform((1, 3,),.0,1.0))
b3 = tf.Variable(tf.random_uniform((1, 1,),.0,1.0))

h1=w1@inputs+b1
z1=activation(h1)
h2=w2@z1+b2
z2=activation(h2)
h3=w3@z2+b3
output=h3

这段代码中，赋予了一个(10,1)的输入数组和(1,1)的标签，和初始在(0,1)随机均匀分布的权重和偏置。有3个需要注意的地方：

tf.placeholder表示一个占位数，等待运行时填值。这和tensorflow的静态图机制有关，tensorflow所有的值初始化和运算都在一个会话（Session）中，这一点大大提升了网络创建的速度，也利于运行时分配显存和分布式训练，但调试比较麻烦（最近tensorflow推出了eager模式，模仿pytorch的动态图机制，详情）。下面是tensorflow的数据在静态图中运算方式。
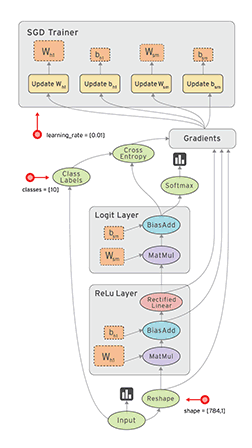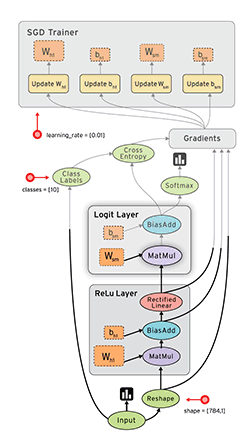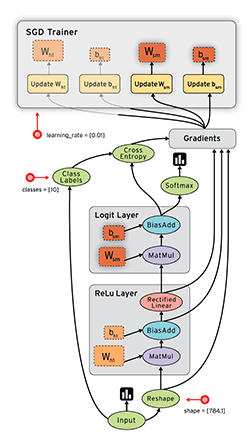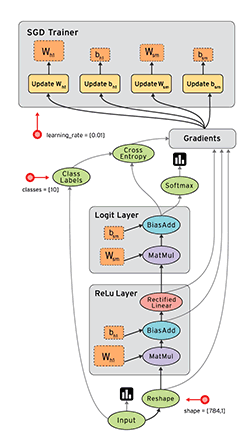
tf.Variable表示可以训练的参数（默认trainable=True），该参数在运行中是可以改变的。如果仅使用tf.random_uniform或tf.constant，那么这个参数是一个固定常量，无法在训练过程中改变。
@是python3中矩阵乘法的操作符。

2.激活和损失函数

2.1激活函数

激活函数赋予了深度网络深层和非线性的能力。假设网络中去掉激活函数，那么隐藏层就会变成这样：

h_{1} = w_{1} * i + b_{1} h_{2} = w_{2} * h_{1} + b_{2} = w_{2} * (w_{1} * i + b_{1}) + b_{2} = w_{2} * w_{1} * i + w_{1} * b_{1} + b_{2} = W * i + B

$h_{1}=w_{1}*i+b_{1}\\ h_{2}=w_{2}*h_{1}+b_{2}=w_{2}*(w_{1}*i+b_{1})+b_{2}=\\ w_{2}*w_{1}*i+w_{1}*b_{1}+b_{2}=W*i+B$
看到了吗?如果没有激活函数，二层隐藏层实际就成了一层。 没有激活函数，加深网络是没有意义的。
另外，激活函数还给予了网络非线性的能力。比如使用一个sigmoid的激活函数（

y = \frac{1}{e^{- x} + 1}

$y=\frac{1}{e^{-x}+1}$ ），函数图形如下：

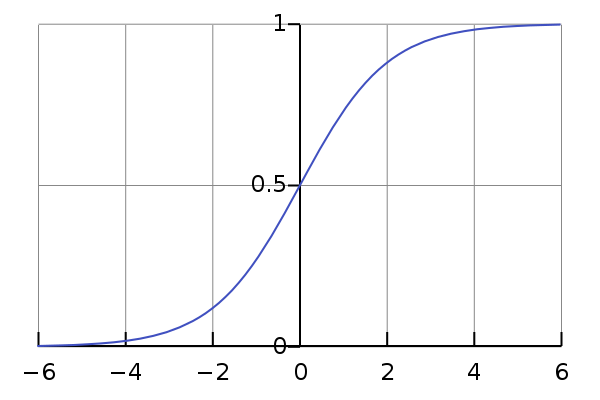
这时我们输入一个[-2,-1,0,1,2]的数组，输出就变为[ 0.12,0.27,0.5,0.73,0.88]。不仅输入变成了(0,1)间的数（正则化），而且分布变为两段密，中间疏（非线性）。
在麻雀网络中，我们使用elu作为激活函数，它的好处有很多。你也可以使用relu,sigmoid或tanh作为激活函数，下章会讲一下它们的优劣。elu函数定义如下：

σ (x) = {\begin{matrix} x & , x \geq 0 \\ e^{x} - 1 & , x < 0 \end{matrix} σ^{'} (x) = {\begin{matrix} 1 & , x \geq 0 \\ e^{x} & , x < 0 \end{matrix}

$\sigma (x)=\left\{\begin{matrix} x & ,x\geq 0\\ e^{x}-1 & ,x<0 \end{matrix}\right.\\ \sigma' (x)=\left\{\begin{matrix} 1 & ,x\geq 0\\ e^{x} & ,x<0 \end{matrix}\right.$
这里需要额外求出激活函数的导数，便于后面反向传播使用。这段公式的tensorflow实现如下：

activation=lambda x:tf.where(tf.greater(x,0),x,tf.exp(x)-1.0)
activation_del=lambda x:tf.where(tf.greater(x,0),tf.ones_like(x,tf.float32),tf.exp(x))

其中：
- lambda是python中的匿名函数，你也可以使用def关键词来定义，这是完全等价的。
- tf.where相当于我们常用的if，tf.where(a,b,c)满足a条件的选择b，不满足的选择c。注意tf.where在自动求导中是没有梯度的。

2.2损失函数

损失函数是在深度学习中常常提到的一个概念，通俗地讲，它定义了网络要优化的目标，损失越小，代表输出和目标越接近。损失函数有很多，比如L1,L2,logit等，下次讲一下它们的区别。本文采用L2损失函数，就是平常讲的平方函数:

E = \frac{1}{2} * (o - l a b e l)^{2} E^{'} = o - l a b e l

$E=\frac{1}{2}*(o-label)^{2}\\ E'=o-label$
同样求出了它的导数备用。tensorflow实现如下：

loss=1/2*tf.pow(output-labels,2)
dloss=output-labels

3.反向传播

反向传播算法是深度神经网络能实现的基础，也是DNN中相对最难的部分。反向传播将损失反向累加到权重和偏置上，使下一次的网络运行结果更靠近我们的预期。为什么要使用反向传播算法呢？因为使用前向计算误差的会有大量的冗余计算。在整段网络中，需要更新（训练）的参数有6个，分别是 $w_{1},b_{1},w_{2},b_{2},w_{3},b_{3}$ 。根据链式法则，对它们求导过程如下：

▽ b_{3} = \frac{\partial E}{\partial b_{3}} = \frac{\partial E}{\partial o} * \frac{\partial o}{\partial b_{3}} ▽ w_{3} = \frac{\partial E}{\partial w_{3}} = \frac{\partial E}{\partial o} * \frac{\partial o}{\partial w_{3}} ▽ b_{2} = \frac{\partial E}{\partial b_{2}} = \frac{\partial E}{\partial z_{2}} * \frac{\partial z_{2}}{\partial b_{2}} ▽ w_{2} = \frac{\partial E}{\partial w_{2}} = \frac{\partial E}{\partial z_{2}} * \frac{\partial z_{2}}{\partial w_{2}} ▽ b_{1} = \frac{\partial E}{\partial b_{1}} = \frac{\partial E}{\partial z_{1}} * \frac{\partial z_{1}}{\partial b_{1}} ▽ w_{1} = \frac{\partial E}{\partial w_{1}} = \frac{\partial E}{\partial z_{1}} * \frac{\partial z_{1}}{\partial w_{1}}

$\\\bigtriangledown b_{3}=\frac{\partial E}{\partial b_{3}}=\frac{\partial E}{\partial o}*\frac{\partial o}{\partial b_{3}} \\ \bigtriangledown w_{3}=\frac{\partial E}{\partial w_{3}}=\frac{\partial E}{\partial o}*\frac{\partial o}{\partial w_{3}}\\ \\\bigtriangledown b_{2}=\frac{\partial E}{\partial b_{2}}=\frac{\partial E}{\partial z_{2}}*\frac{\partial z_{2}}{\partial b_{2}} \\ \bigtriangledown w_{2}=\frac{\partial E}{\partial w_{2}}=\frac{\partial E}{\partial z_{2}}*\frac{\partial z_{2}}{\partial w_{2}}\\ \\\bigtriangledown b_{1}=\frac{\partial E}{\partial b_{1}}=\frac{\partial E}{\partial z_{1}}*\frac{\partial z_{1}}{\partial b_{1}} \\ \bigtriangledown w_{1}=\frac{\partial E}{\partial w_{1}}=\frac{\partial E}{\partial z_{1}}*\frac{\partial z_{1}}{\partial w_{1}}\\$
这时有一个中间变量，也就是损失的梯度E对激活函数的输入求导，这个变量很关键，假设这个变量为

δ_{n}

$\delta_{n}$ ,那么有:

δ_{n} = \frac{\partial E}{\partial z_{n}}

$\delta_{n}=\frac{\partial E}{\partial z_{n}}$
因为输出层没有激活函数，所以实际上

z_{3} = o, δ_{3} = \frac{\partial E}{\partial o} = o - l a b e l

$z_{3}=o,\delta_{3}=\frac{\partial E}{\partial o}=o-label$ 。
再仔细观察前向预测部分的公式，可以得到：

δ_{2} = \frac{\partial E}{\partial z_{3}} * \frac{\partial z_{3}}{\partial z_{2}} = \frac{\partial E}{\partial o} * \frac{\partial o}{\partial z_{2}} = w_{3}^{T} δ_{3} σ^{'} (h_{2}) δ_{1} = \frac{\partial E}{\partial z_{2}} * \frac{\partial z_{2}}{\partial z_{1}} = w_{2}^{T} δ_{2} σ^{'} (h_{1})

$\delta_{2}=\frac{\partial E}{\partial z_{3}}*\frac{\partial z_{3}}{\partial z_{2}}=\frac{\partial E}{\partial o}*\frac{\partial o}{\partial z_{2}}=w_{3}^{T}\delta_{3}\sigma '(h_{2})\\ \delta_{1}=\frac{\partial E}{\partial z_{2}}*\frac{\partial z_{2}}{\partial z_{1}}=w_{2}^{T}\delta_{2}\sigma' (h_{1})\\$
基于上式，在无限长的隐藏层中，有

δ_{n} = \frac{\partial E}{\partial z_{n + 1}} * \frac{\partial z_{n + 1}}{\partial z_{n}} = w_{n + 1}^{T} δ_{n + 1} σ^{'} (h_{n})

$\delta_{n}=\frac{\partial E}{\partial z_{n+1}}*\frac{\partial z_{n+1}}{\partial z_{n}}=w_{n+1}^{T}\delta_{n+1}\sigma' (h_{n})$ 。结合

w_{3}, b_{3}

$w_{3},b_{3}$ 的求导过程，我们可以得到

▽ b_{n} = δ_{n} * 1, ▽ w_{n} = δ_{n} z_{n - 1}^{T}

$\bigtriangledown b_{n}=\delta_{n}*1,\bigtriangledown w_{n}=\delta_{n}z_{n-1}^{T}$ ，从而最终求出权重和偏置的梯度。在实际操作中，一般是先反向求这个中间变量，再分别求

w, b

$w,b$ 的梯度，达到去除冗余计算的目的。
用tensorflow反向求梯度代码如下：

d_th3=dloss
d_th2=tf.transpose(w3)@d_th3*activation_del(h2)
d_th1=tf.transpose(w2)@d_th2*activation_del(h1)
d_w3=d_th3@tf.transpose(z2)
d_w2=d_th2@tf.transpose(z1)
d_w1=d_th1@tf.transpose(inputs)

4.梯度优化

得到了梯度之后，怎么将其更新给参数呢?一般采用一些梯度优化方法，比如梯度下降、SGD、BSGD、动量、Adam等，如何选择一个好的优化算法是非常重要的工作，我们以后再分析这些方法。这里使用一种最简单的优化方法——梯度下降法。梯度下降法优化公式如下:

x^{t + 1} = x_{t} - η ▽ x^{t}

$x^{t+1}=x_{t}-\eta \bigtriangledown x^{t}$
其中，

η

$\eta$ 表示学习率，这是深度神经网络中最常见的超参数（需要手工调整的参数）。通过调节学习率，你可以调整参数拟合的速度，避免陷入局部极值和震荡。
这用tensorflow实现非常简单，毕竟tensorflow主要就是干优化的活：

optimize=[
    tf.assign(b3,tf.subtract(b3,lr*d_th3)),
    tf.assign(w3,tf.subtract(w3,lr*d_w3)),
    tf.assign(b2,tf.subtract(b2,lr*d_th2)),
    tf.assign(w2,tf.subtract(w2,lr*d_w2)),
    tf.assign(b1,tf.subtract(b1,lr*d_th1)),
    tf.assign(w1,tf.subtract(w1,lr*d_w1))
]

其中:

tf.assign表示赋值操作。
tf.subtract表示减，tf.subtract(b3,lr*d_th3)的写法完全等价于b3-lr*d_th3。

至此为止，我们已经完成了所有网络定义的任务，是时候展现一下神经网络的威力了。

5.尝试用它解一道数学应用题

训练神经网络，实际上就是求映射 $f()$ ，这个映射满足对于输入的x，得到希望的y，也就是 $f(x)->y$ 。具体的讲，给一段数据，网络输出它的类别，并且和真实的类别差距尽量小。
那么我们就来设计一个任务，随机给的10个数字求和，并除以2。用python实现非常简单：

import numpy as np

src=np.random.rand(10,1)*5
label=np.sum(src)/2

实现这样一个任务，一秒都不需要。但问题难在哪里呢？很多时候，人们只有这样一堆样本和结果，但不知道这个函数（映射）到底是什么。但人们希望在给定另外一批样本时，计算机也能算出符合预期的结果。这就是深度神经网络的任务，它有非线性能力拟合出一个逼近真实映射的函数，网络越深，这种拟合能力越强。这种能力有多强呢？ Hava Siegelmann和Eduardo D. Sontag的工作证明了，一个具有有理数权重值的特定递归结构（与全精度实数权重值相对应）相当于一个具有有限数量的神经元和标准的线性关系的通用图灵机(On the Computational Power of Neural Nets)。这说明神经网络可以模拟基本数学运算、逻辑控制、递归计算等过程。我们利用它来解决这个问题。

tensorflow代码如下：

train_num=100
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(train_num):
        src,label=feed_data()
        sess.run(optimize,feed_dict={inputs:src,labels:label})
        print(sess.run(loss, feed_dict={inputs: src,labels:label}))
    src, label = feed_data()
    print(src,sess.run(output,feed_dict={inputs:src}),label)

tensorflow代码都是在会话(session)上运行的，所以首先创建一个会话。
tf.global_variables_initializer()会将默认网络中的参数进行初始化，也就是把权重和偏置的初值固定，之前我们定义了初值是在（0，1）内平均分布的随机值。
会话中运行optimize，该运算我们之前定义过，就是用梯度下降法更新权重和偏置。因为神经网络正向预测和反向传播分别需要输入和标签，所以将两个数组反馈给网络(feed_dict)。
训练100次之后，用新的权重和偏置取预测一段数据，并得到结果。
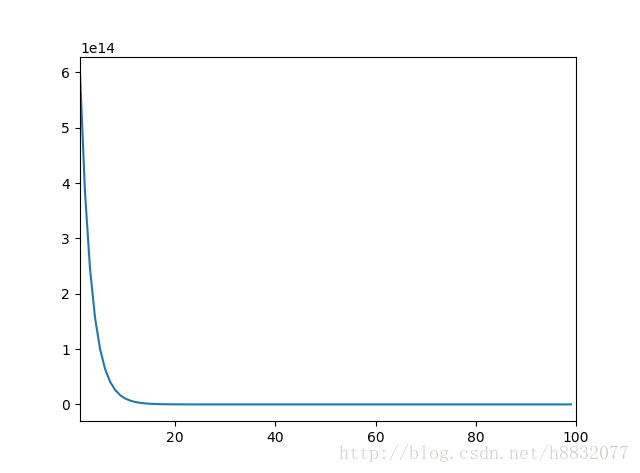
运行损失如下(y轴损失，x轴训练次数)：

最后测试时，随机输入一段10x1的数：

[[ 3.52792097] [ 3.44786069] [ 0.62893607] [ 3.28180785] [ 0.27414099] [ 4.69292455] [ 1.85201189] [ 4.87615163] [ 0.82248265] [ 0.46025282]]

真实的结果应该是：11.93224506
最后我们得到结果是：13.4375
我们发现训练100次的模型预测结果已经和真实结果接近了（值差了1.5,初始网络预测结果和真实结果差了1e7），说明深度网络确实有逼近一个连续函数的能力。

完整的麻雀网络代码如下：

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

lr=0.05
train_num=100

w1 = tf.Variable(tf.random_uniform((7, 10,),0.0,1.0))
b1 = tf.Variable(tf.random_uniform((7, 1,),.0,1.0))
w2 = tf.Variable(tf.random_uniform((3, 7,),.0,1.0))
b2 = tf.Variable(tf.random_uniform((3, 1,),.0,1.0))
w3 = tf.Variable(tf.random_uniform((1, 3,),.0,1.0))
b3 = tf.Variable(tf.random_uniform((1, 1,),.0,1.0))

inputs=tf.placeholder(tf.float32,(10,1))
labels=tf.placeholder(tf.float32,(1,1))
activation=lambda x:tf.where(tf.greater(x,0),x,tf.exp(x)-1.0)
activation_del=lambda x:tf.where(tf.greater(x,0),tf.ones_like(x,tf.float32),tf.exp(x))

h1=w1@inputs+b1
z1=activation(h1)
h2=w2@z1+b2
z2=activation(h2)
h3=w3@z2+b3
output=h3

loss=1/2*tf.pow(output-labels,2)
dloss=output-labels

d_th3=dloss
d_th2=tf.transpose(w3)@d_th3*activation_del(h2)
d_th1=tf.transpose(w2)@d_th2*activation_del(h1)
d_w3=d_th3@tf.transpose(z2)
d_w2=d_th2@tf.transpose(z1)
d_w1=d_th1@tf.transpose(inputs)

optimize=[
    tf.assign(b3,tf.subtract(b3,lr*d_th3)),
    tf.assign(w3,tf.subtract(w3,lr*d_w3)),
    tf.assign(b2,tf.subtract(b2,lr*d_th2)),
    tf.assign(w2,tf.subtract(w2,lr*d_w2)),
    tf.assign(b1,tf.subtract(b1,lr*d_th1)),
    tf.assign(w1,tf.subtract(w1,lr*d_w1))
]


def feed_data():
    src=np.random.rand(10,1)*5
    label=np.sum(src)/2
    return src,np.reshape(label,(1,1))

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    ans=[]
    for i in range(train_num):
        src,label=feed_data()
        _,l=sess.run([optimize,loss],feed_dict={inputs:src,labels:label})
        print(l)
        ans+=[l]
    plt.plot(np.squeeze(np.array(ans)))
    plt.xlim(1,100)
    plt.show()
    src, label = feed_data()
    print(src,sess.run(output,feed_dict={inputs:src}),label)

建议读者按自己能力依次完成以下额外任务：

用numpy重写麻雀网络，加深对网络的理解。
麻雀网络运行后，输出有几率变为nan，即梯度爆炸；也有可能变为0，即梯度消失。请尝试通过改变参数初始化，加入正则化、改变激活函数、更改网络结构、调整优化算法等方式解决这个问题。
尝试用深度神经网络解决逻辑判断和递归问题。

最后祝您身体健康，再见！