机器学习进阶之（四）XGBoost-LightGBM

1. 回顾XGboost

XGBoost在竞赛与工业界都使用频繁。XGBoost是决策树的一种，那么要使用决策树过程，下面有两个弱分类器，一个以年龄性别，另一个以是否使用电脑，这是一种集成的思想，我们利用叶子节点与权值来表示预测值。

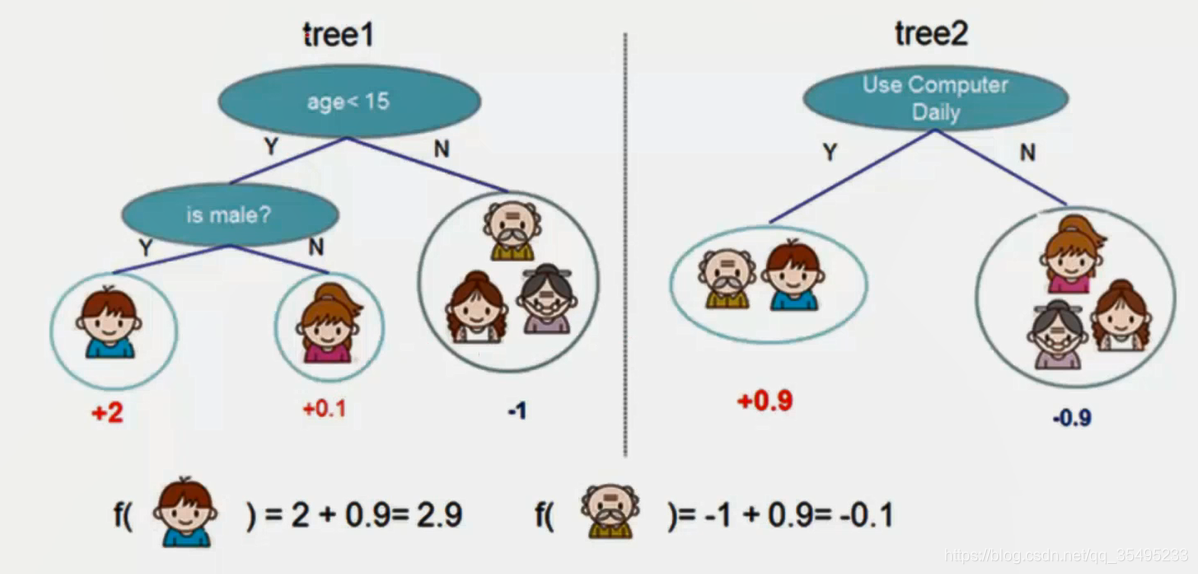
1.1 Boosting思想

Boosting是一个加法模型，从常数开始迭代，每一轮迭代增加一个函数，每次新添加的函数是基于以往所有的学习结果的和与真实值之间的残差上学习模型。
$\vec y_i^{(0)} = 0$ $\vec y_i^{(1)}=f_1(x_i)=\vec y_i^{(0)} + f_1(x_i)$ $\vec y_i^{(2)}=f_1(x_i)+f_2(x_i)=\vec y_i^{(1)}+f_2(x_i)$ $...$ $\vec y_i^{(t)}=\sum_{k=1}^t f_k(x_i)=\vec y_i^{(t-1)}+f_t(x_i)$

1.2 XGBoost损失函数

XGBoost需要对每棵树都进行综合考虑，优化目标是一个损失函数。
我们的目标函数是： $l(y_i, \overline y_i)=(y_i - \overline y_i)^2$，那么我们如何求 最优函数呢？ $F^*(\vec x)=argminE_{(x,y)}[L(y,F(\vec x))]$集成算法表示： $\vec y_i =\sum_{k=1} ^ K f_k(x_i), f \in F$

XGBoost其最核心最本质的解决思路：我们构建一棵树，再构建一棵树，是有一个明显的提升的，所以在每加一棵树时，效果都有明显的提升。
$\vec y_i^{(0)} = 0$ $\vec y_i^{(1)}=f_1(x_i)=\vec y_i^{(0)} + f_1(x_i)$ $\vec y_i^{(2)}=f_1(x_i)+f_2(x_i)=\vec y_i^{(1)}+f_2(x_i)$ $...$ $\vec y_i^{(t)}=\sum_{k=1}^t f_k(x_i)=\vec y_i^{(t-1)}+f_t(x_i)$
其中， $\vec y_i^{(t)}$是第 $t$轮模型预测， $\vec y_i^{(t-1)}$保留前面 $t-1$轮模型预测， $f_t(x_i)$为加入的一个新函数，那么没加入一棵树都有一定的损失函数，我们可以将 $f_{x}(x_i)$看成是一棵树，每加入一棵新的树所构造出来的模型。

1.3 正则化构建公式

根据决策树来构建树，那么我们需要限制叶子结点的个数，那么我们在做损失函数（也就是目标函数）时，考虑加入正则化项来防止过拟合。这里采用L2正则化，需要重新定义 $\Omega(f_t)=\gamma T + \frac{1}{2} \sum_{j=1}^T \omega_j^2$

这个 $\Omega$表示对于这个XGboost来说，这个正则化惩罚项是如何表示的，目标函数为：
$Obj^{(t)}=\sum_{i=1}^{n}(y_i-(\vec y_i^{(t-1)} + f_t(x_i)))$ $=\sum_{i=1}^n [2(\vec y_i^{(t-1)}+f_t(x_i)+f_t(x_i)^2)]+\Omega(f_t)+constant$，也就是不断修正我们全部要预测的残差达到模型最准确的值。

1.4 泰勒展开公式

泰勒公式是一个用函数在某点的的信息描述其附近取值的公式，局部有效性。
$f(x)=∑_{n=0}^{\infin} \frac {f(x_0)^{(n)}}{n!} (x-x_0)^n$
一阶泰勒展开： $f(x) \approx f(x_0) + f'(x_0)(x-x_0)$
二阶泰勒展开： $f(x) \approx f'(x_0)(x-x_0) + \frac{1}{2} f''(x_0)(x-x_0)^2$
假设第 $t$次迭代的为 $x^{(t)}$，则 $t+1$次迭代为： $x^{(t+1)}=x^{(t)}+ Δx$，那么，在 $x^{(t+1)}$处进行泰勒展开，结果为： $f(x^{(t+1)}) \approx f(x^{(t)})+f'(x^{(t)})Δx + \frac{1}{2} f''(x^{(t)})(Δx)^2$

将样本上的遍历转换为叶子节点上的遍历：

1.5 寻找最优分裂点

对于一个叶子节点，如何进行分裂？
$Gain=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma$
公式中每个点如下：

• $\frac{G_L^2}{H_L+\lambda}$：左子树分数
• $\frac{G_R^2}{H_R+\lambda}$：右子树分数
  是右节点的得分值
• $\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}$ 不可分隔的叶子节点的分数
• $- \gamma$：是通过引入额外叶子节点所降低复杂度
  若 $Gain > 0$，那么节点应该分裂，若小于0，则不分裂。

1.6 算法流程

对于上述公式：
$Obj^{(t)} \approx ∑_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t)+const$ $=∑_{j=1}^T [(∑_{i \in j} g_i)w_i + \frac{1}{2}(∑_{i \in I_j}h_i + \lambda)w_j^2]$
其中，关于一阶导数，二阶导数有如下定义，其中 $i$为训练集中的第 $i$个样本， $I_j$为模型中第 $j$个叶子节点中所有的训练样本。
$G_i=∑_{i \in I_j}g_i，H_j=∑_{i \in I_j}h_i$
对于一元二次函数： $argmin_xG_x+\frac{1}{2}Hx^2=-\frac{G}{H},H>0$ $min_xG_x+\frac{1}{2}Hx^2=-\frac{1}{2}\frac{G^2}{H}$因此，对于目标函数进行最小化的时候，即二次函数在对称轴时，取得最值。 $minObj^{(t)}=∑_{j=1}^T[G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2]+\gamma T=\frac{1}{2}∑_{j=1}^T \frac{G_j^2}{H_j+\lambda}+\gamma T$对于正则化项， $w_i$为第 $i$个叶子节点的值。
$\Omega(f_t)=\gamma T+\frac{1}{2}\gamma ∑_{j=1}^T w_j^2$

• $T$：叶子节点的数量
• $∑_{j=1}^T w_j^2$:L2正则化叶子的得分值。

其中，在遍历每个叶子节点的过程时，每次遍历都是一个查看变换的过程。

1.7 实例分析

$Obj$代表了我们指定一棵树的时候，我们在目标上最多减多少分数 $structure score$，可以认为这类似于吉尼系数一样增加对于树结构进行打分的函数，下面是一个具体的打分函数实例：
$G$是一阶导， $H$是二阶导。

2. 回顾LightGBM

2.1 LightGBM模型实例

2.2 LightGBM参数实例

markdown公式参考：
(1). https://www.cnblogs.com/peaceWang/p/Markdown-tian-jia-Latex-shu-xue-gong-shi.html
(2). https://jzqt.github.io/2015/06/30/Markdown中写数学公式/