专题（一）优化算法

1.梯度下降

• 梯度下降是一种优化算法，通过迭代的方式寻找模型的最优参数
  • 所谓最优参数指的是使目标函数达到最小值时的参数；
  • 当目标函数是凸函数时，梯度下降的解是全局最优解；但在一般情况下，梯度下降无法保证全局最优。
• 微积分中使用梯度表示函数增长最快的方向；因此，神经网络中使用负梯度来指示目标函数下降最快的方向。
  • 梯度实际上是损失函数对网络中每个参数的偏导所组成的向量；
  • 梯度仅仅指示了对于每个参数各自增长最快的方向；因此，梯度无法保证全局方向就是函数为了达到最小值应该前进的方向。
  • 梯度的具体计算方法即反向传播。
• 负梯度中的每一项可以认为传达了两个信息：
  • 正负号在告诉输入向量应该调大还是调小（正调大，负调小）
  • 每一项的相对大小表明每个参数对函数值达到最值的影响程度；

1.1 随机梯度下降

基本的梯度下降法每次使用所有训练样本的平均损失来更新参数；

• 因此，经典的梯度下降在每次对模型参数进行更新时，需要遍历所有数据；
• 当训练样本的数量很大时，这需要消耗相当大的计算资源，在实际应用中基本不可行。
• **随机梯度下降（SGD）**每次使用单个样本的损失来近似平均损失

1.2 小批量随机梯度下降

• 为了降低随机梯度的方差，使模型迭代更加稳定，实践中会使用一批随机数据的损失来近似平均损失。
• 使用批训练的另一个主要目的，是为了利用高度优化的矩阵运算以及并行计算框架。

1.2.1 小批量 SGD 的更新过程

1. 在训练集上抽取指定大小 $batchsize$ 的一批数据 ${(x,y)}$
2. 前向传播将这批数据送入网络，得到这批数据的预测值 $y_{pred}$
3. 计算网络在这批数据上的损失，用于衡量 $y_{pred}$ 和 $y$ 之间的距离
4. 反向传播计算损失相对于所有网络中可训练参数的梯度 $g$
5. 将参数沿着负梯度的方向移动，即 $W -= lr * g$

1.2.2 “批”的大小对优化效果的影响

• 较大的批能得到更精确的梯度估计，但回报是小于线性的。
• 较小的批能带来更好的泛化误差，泛化误差通常在批大小为 1 时最好。
  • 因可能是由于小批量在学习过程中带来了噪声，使产生了一些正则化效果 (Wilson and Martinez, 2003)
  • 但是，因为梯度估计的高方差，小批量训练需要较小的学习率以保持稳定性，这意味着更长的训练时间。
• 当批的大小为 2 的幂 时能充分利用矩阵运算操作，所以批的大小一般取 32、64、128、256 等。

1.2.3 随机梯度下降存在的问题

• 随机梯度下降（SGD）放弃了梯度的准确性，仅采用一部分样本来估计当前的梯度；因此 SGD 对梯度的估计常常出现偏差，造成目标函数收敛不稳定，甚至不收敛的情况。
• 无论是经典的梯度下降还是随机梯度下降，都可能陷入局部极值点；除此之外，SGD 还可能遇到“峡谷”和“鞍点”两种情况
  • 峡谷类似一个带有坡度的狭长小道，左右两侧是“峭壁”；在峡谷中，准确的梯度方向应该沿着坡的方向向下，但粗糙的梯度估计使其稍有偏离就撞向两侧的峭壁，然后在两个峭壁间来回震荡。
  • 鞍点的形状类似一个马鞍，一个方向两头翘，一个方向两头垂，而中间区域近似平地；一旦优化的过程中不慎落入鞍点，优化很可能就会停滞下来。
    

1.2.4 随机梯度下降的改进方向

• SGD 的改进遵循两个方向：惯性保持和环境感知
  • 惯性保持指的是加入动量 SGD 算法：Momentum方法
  • 环境感知指的是根据不同参数的一些经验性判断，自适应地确定每个参数的学习速率：自适应学习率的优化算法

例如：训练词向量的例子

• 不同词出现的频率是不同的，数据的稀疏性会影响其参数的稀疏性；
• 具体来说，对低频词如果不加措施，其参数的梯度在多数情况下为 0；换言之，这些参数更新的频率很低，导致难以收敛。
• 在实践中，我们希望学习低频词的参数时具有较大的学习率，而高频词其参数的更新幅度可以小一些。

2. 动量（Momentum）算法

2.1 带动量的 SGD

• 引入动量（Momentum）方法一方面是为了解决“峡谷”和“鞍点”问题；一方面也可以用于SGD 加速，特别是针对高曲率、小幅但是方向一致的梯度。
  • 如果把原始的 SGD 想象成一个纸团在重力作用向下滚动，由于质量小受到山壁弹力的干扰大，导致来回震荡；或者在鞍点处因为质量小速度很快减为 0，导致无法离开这块平地。
  • 动量方法相当于把纸团换成了铁球；不容易受到外力的干扰，轨迹更加稳定；同时因为在鞍点处因为惯性的作用，更有可能离开平地。
  • 动量方法以一种廉价的方式模拟了二阶梯度（牛顿法）
    

2.1.1 参数更新公式

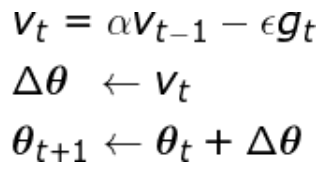
从形式上看， 动量算法引入了变量v充当速度角色，以及相相关的超参数α。
原始 SGD 每次更新的步长只是梯度乘以学习率；现在，步长还取决于历史梯度序列的大小和排列；当许多连续的梯度指向相同的方向时，步长会被不断增大；

2.1.2 动量算法描述

- 如果动量算法总是观测到梯度g，那么它会在−g方向上不断加速，直到达到最终速度。

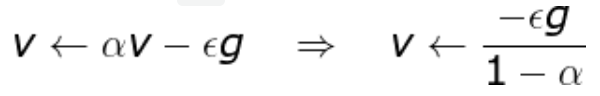
- 在实践中， α的一般取0.5, 0.9, 0.99，分别对应最大 2 倍、10 倍、100 倍的步长
- 和学习率一样，α也可以使用某种策略在训练时进行自适应调整；一般初始值是一个较小的值，随后会慢慢变大。

2.2 NAG 算法（Nesterov 动量）

• NAG 把梯度计算放在对参数施加当前速度之后。
• 这个“提前量”的设计让算法有了对前方环境“预判”的能力。Nesterov 动量可以解释为往标准动量方法中添加了一个修正因子。
• NAG 算法描述
  

3. 自适应学习率的优化算法

3.1 AdaGrad

• 该算法的思想是独立地适应模型的每个参数：具有较大偏导的参数相应有一个较大的学习率，而具有小偏导的参数则对应一个较小的学习率
• 具体来说，每个参数的学习率会缩放各参数反比于其历史梯度平方值总和的平方根
• AdaGrad 算法描述
  
  • 注意：全局学习率ϵ并没有更新，而是每次应用时被缩放

3.1.1 AdaGrad 存在的问题

• 学习率是单调递减的，训练后期学习率过小会导致训练困难，甚至提前结束
• 需要设置一个全局的初始学习率

3.2 RMSProp

• RMSProp主要是为了解决AdaGrad方法中学习率过度衰减的问题—— AdaGrad 根据平方梯度的整个历史来收缩学习率，可能使得学习率在达到局部最小值之前就变得太小而难以继续训练；
• RMSProp 使用指数衰减平均（递归定义）以丢弃遥远的历史，使其能够在找到某个“凸”结构后快速收敛；此外，RMSProp 还加入了一个超参数ρ用于控制衰减速率。
• 具体来说（对比 AdaGrad 的算法描述），即修改r为
  
  其中E表示期望，即平均；δ为平滑项，具体为一个小常数，一般取1e-8 ~ 1e-10（Tensorflow 中的默认值为1e-10）
  RMSProp 建议的初始值：全局学习率ϵ=1e-3，衰减速率ρ=0.9

3.2.1 RMSProp 算法描述

3.2.2 带 Nesterov 动量的 RMSProp

• 经验上，RMSProp 已被证明是一种有效且实用的深度神经网络优化算法。
• RMSProp 依然需要设置一个全局学习率，同时又多了一个超参数（推荐了默认值）。

• 3.3 AdaDelta

• AdaDelta 和 RMSProp 都是为了解决 AdaGrad 对学习率过度衰减的问题而产生的。
• AdaDelta 和 RMSProp 是独立发现的，AdaDelta 的前半部分与 RMSProp 完全一致；
• AdaDelta 进一步解决了 AdaGrad 需要设置一个全局学习率的问题
• 具体来说，即
  
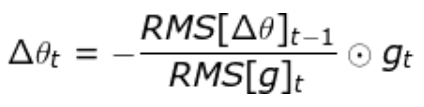
  此时，AdaDelta 已经不需要设置全局学习率了

3.4 Adam

• Adam 在 RMSProp 方法的基础上更进一步：
  • 除了加入历史梯度平方的指数衰减平均（r）外，
  • 还保留了历史梯度的指数衰减平均（s），相当于动量。
  • Adam 行为就像一个带有摩擦力的小球，在误差面上倾向于平坦的极小值。

3.4.1 Adam 算法描述

偏差修正

• 注意到，s和r需要初始化为 0；且 ρ1 和 ρ2 推荐的初始值都很接近 1（0.9 和 0.999）
• 这将导致在训练初期s和r都很小（偏向于 0），从而训练缓慢。
• 因此，Adam通过修正偏差来抵消这个倾向。

3.4.2 AdaMax

• Adam的一个变种，对梯度平方的处理由指数衰减平均改为指数衰减求最大值

3.4.3 Nadam

• Nesterov 动量版本的 Adam

4. 如何选择优化算法

• SGD各优化方法在损失曲面上的表现
  
• SGD各优化方法在鞍点处上的表现
  

5. 基于二阶梯度的优化算法

5.1 牛顿法

• 梯度下降使用的梯度信息实际上是一阶导数
• 牛顿法除了一阶导数外，还会使用二阶导数的信息
• 根据导数的定义，一阶导描述的是函数值的变化率，即斜率；二阶导描述的则是斜率的变化率，即曲线的弯曲程度——曲率

5.1.1 几何理解

• 牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面；而梯度下降法是用一个平面去拟合当前的局部曲面。
• 通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

5.1.2 通俗理解

• 比如你想找一条最短的路径走到一个盆地的最底部，
• 梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步；
• 牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。
• 所以，牛顿法比梯度下降法看得更远，能更快地走到最底部。

5.1.3 牛顿法的优缺点

• 优点
  • 收敛速度快，能用更少的迭代次数找到最优解
• 缺点
  • 每一步都需要求解目标函数的 Hessian 矩阵的逆矩阵，计算复杂