大致题意: 有一个\(n\)行\(m\)列的网格图,让你给每一条边设置一个通过次数(\(\ge1\)),使其成为欧拉回路,且通过次数总和最小。
初始化
首先,由于通过次数\(\ge1\),因此首先必然设置每条边通过次数为\(1\)。
对于一个\(n\)行\(m\)列的网格图,共有\(n(m-1)+m(n-1)\)条边,如下图:
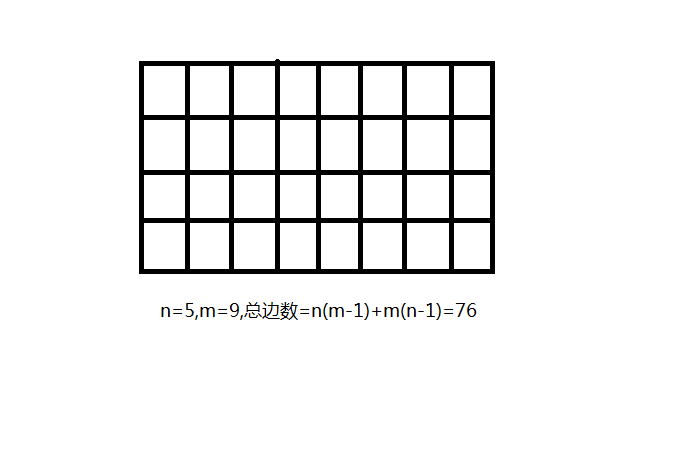
所以,初始化\(ans\)为\(n(m-1)+m(n-1)\)。
仔细观察上图,可以发现,中间的点以及四个角落的点都为偶点,因此只需给边上的点连边,使其全为偶点即可。
但又需要分类讨论。
当\(n,m\)都为偶数时
如图所示:
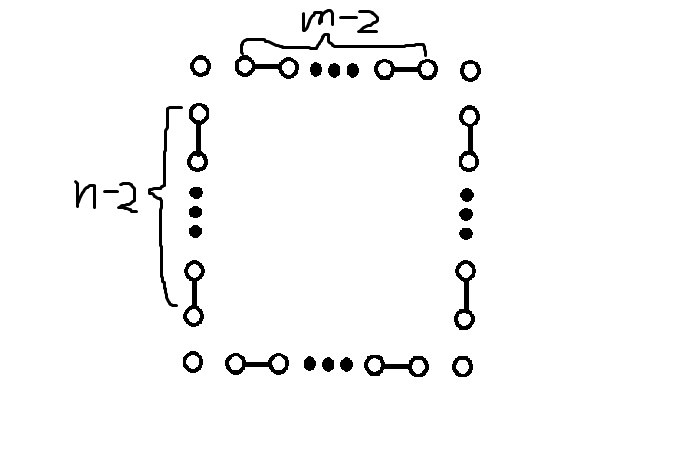
考虑将两条邻边作为一组。
则我们可以将同一组中两条边的交点向旁边两点连边,这样交点仍为偶点,而交点旁边这两个点也变成了偶点。
这样每条边上剩下的奇点个数就为偶数了。
则我们依然对相邻的两点之间连一条边,这样就可以使所有点都变成偶点了。
加的边数为:
\[2(\frac{n-2}2+\frac{m-2}2)=n+m-4\]
当\(n,m\)都为奇数时
如图所示:

考虑将两条邻边作为一组。
则我们可以将同一组中两条边的交点向旁边两点连边,这样交点仍为偶点,而交点旁边这两个点也变成了偶点。
这样每条边上剩下的奇点个数就为偶数了。
则我们依然对相邻的两点之间连一条边,这样就可以使所有点都变成偶点了。
加的边数为:
\[2(\frac{n-3}2+\frac{m-3}2)+4=n+m-2\]
当\(n,m\)一奇一偶时
如图所示(假设\(n\)为奇数,\(m\)为偶数):

我们把两条奇数边靠同一边的一个点一起向角上的点连边,然后剩下的\(n-3\)个点在相邻的两点之间连一条边。
其中被连过边的角上两点变成奇点,因此需向这条偶数边上两侧的点连一条边。此时这条边上剩下的\(m-4\)个点再在相邻的两点之间连一条边。
然后可以发现还有一条边上始终没有连过边,则直接在相邻的两点之间连一条边即可。
加的边数为:
\[2*\frac{n-3}2+\frac{m-4}2+\frac{m-2}2+4=n+m-2\]
不难发现\(m\)为奇数,\(n\)为偶数时同理。
当\(n=2\)或\(m=2\)时
上面的分类讨论看似包含了所有情况,实则还有一种特殊情况没有考虑,即\(n=2\)或\(m=2\)时。
如图所示:
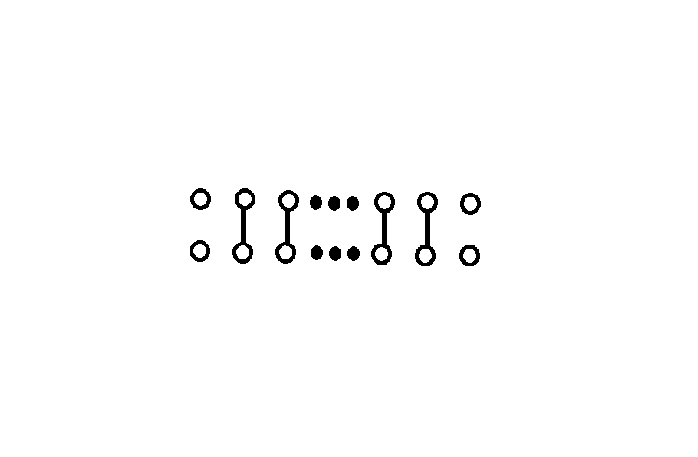
不难发现,\(n\)或\(m\)若有一个为\(2\),则另一边的点可以与对边上的点两两相连。
加的边数为:
\[n-2\ or\ m-2\]
总结
因此,对于给定的\(n\)和\(m\),先初始化\(ans\)为\(n(m-1)+m(n-1)\)。
接下来,特判\(n=2\)或\(m=2\)的情况。
然后分奇偶性讨论,从上面的分析可以发现,在有至少一个奇数时加边数为\(n+m-2\),若皆为偶数则加边数可以减\(2\)。
具体实现见代码。
代码
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
using namespace std;
int n,m;
int main()
{
scanf("%d%d",&n,&m);RI ans=n*(m-1)+m*(n-1);//读入+初始化ans
if(n==2) return printf("%d",ans+m-2),0;if(m==2) return printf("%d",ans+n-2),0;//特判n=2或m=2的情况
return ans+=n+m-2,!(n&1)&&!(m&1)&&(ans-=2),printf("%d",ans),0;//考虑一般情况,分奇偶性讨论
}