有限元笔记1-高斯积分

在有限元计算中，积分运算是非常重要的一种运算，比如刚度矩阵的运算（以二维问题为例）：

[K] = \int \int A [B] T [D] [B] h d x d y

$\left[ K \right] = {\int\!\!\!\int_A {\left[ B \right]} ^T}\left[ D \right]\left[ B \right]hdxdy$ 需要频繁地使用积分运算。

而在所有的积分方法中，最常采用的就是高斯点积分法。在针对刚度矩阵的积分计算中，高斯点的选取对积分刚度矩阵的计算结果有着非常重要的影响(具体可以参见’减缩积分’)。一般某一个方向积分的高斯点数 $n$ 和该方向的单元阶次 $p$ 满足 $N=int[(p+1)/2]+1$ 的经验关系。

所以在开始有限元的学习前非常有必要了解下高斯积分计算。

高斯积分的原理是，讲积分区间 $[a,b]$ 转换为 $[-1,1]$ ，然后利用高斯点和对应的权值来讲积分运算转换为离散形式的求和运算以得到积分结果，具体积分公式如下（以一维积分为例）：

\int 1 - 1 f (ξ) d ξ = \sum i = 1 n H i f (ξ i)

$\int_{ - 1}^1 {f\left( \xi \right)} d\xi = \sum\limits_{i = 1}^n {{H_i}f\left( {{\xi _i}} \right)}$

一般常用2点高斯积分或者3点高斯积分，其部分的取值情况如下所示：

n	$\pm {\xi _i}$	${H_i}$
2	0.5773502692	1.000000000
3	0.7745966692,0.0	0.55555555556,0.88888888889
4	0.8611363116,0.3399810436	0.3478548451,0.6521451549

这里本文分享一个可以生成任意数目高斯点的程序，代码如下：

void Lgwt(int n,double a,double b,double *gpt,double *gwt)
{
    int i,j,k;
    int n1,n2;
    double *xu,*y,*y0,**L,*Lp,pi,eps,temp;
    eps=1.e-8;

    pi=4.0*atan(1.0);
    n=n-1;n1=n+1;n2=n+2;

    xu=new double[n1+1];
    y=new double[n1+1];
    y0=new double[n1+1];
    L=new double*[n1+1];
    Lp=new double[n1+1];
    for(i=0;i<=n1;i++)
    {
        L[i]=new double[n2+1];
    }

    for(i=1;i<=n1;i++)
    {
        xu[i]=-1.0+(i-1)*2.0/(n1-1);
        y[i]=cos((2*(i-1)+1.0)*pi/(2*n+2))+
        (0.27/n1)*sin(pi*xu[i]*n/n2);
        y0[i]=2.0;
    }

    for(i=0;i<=n1;i++)
    {
        for(j=0;j<=n2;j++)
        {
            L[i][j]=0.0;
        }
        Lp[i]=0.0;
    }
    while(1)
    {
        temp=fabs(y[1]-y0[1]);
        for(i=2;i<=n1;i++)
        {
            if(fabs(y[i]-y0[i])>temp)
            {
                temp=fabs(y[i]-y0[i]);
            }
        }
        if(temp<1.e-12)
            break;

        for(i=1;i<=n1;i++)
        {
            L[i][1]=1.0;
            L[i][2]=y[i];
        }
        for(i=1;i<=n1;i++)
        {
            for(k=2;k<=n1;k++)
            {
                L[i][k+1]=((2*k-1)*y[i]*L[i][k]-(k-1)*L[i][k-1])/k;
            }
        }
        for(i=1;i<=n1;i++)
        {
            Lp[i]=n2*(L[i][n1]-y[i]*L[i][n2])/(1.0-y[i]*y[i]);
        }
        for(i=1;i<=n1;i++)
        {
            y0[i]=y[i];
            y[i]=y0[i]-L[i][n2]/Lp[i];
        }
    }

    for(i=1;i<=n1;i++)
    {
        gpt[i-1]=(a*(1.0-y[i])+b*(1.0+y[i]))/2.0;
        gwt[i-1]=(b-a)/((1.0-y[i]*y[i])*Lp[i]*Lp[i])*((n2*n2*1.0)/(n1*n1*1.0));
    }

    delete []xu;
    delete []y;
    delete []y0;
    delete []Lp;
    for(i=0;i<=n1;i++)
    {
        delete []L[i];
    }
    delete []L;

}

针对一维、二维积分情形，本文分别选取了

\int b a x d x = b 2 - a 2 2

$\int_a^b {xdx} = {{{b^2} - {a^2}} \over 2}$
和

\int x b x a \int y b y a x y d x d y = ( x 2 b - x 2 a ) ( y 2 b - y 2 a ) 4

$\int_{{x_a}}^{{x_b}} {\int_{{y_a}}^{{y_b}} {xydxdy} } = {{\left( {x_b^2 - x_a^2} \right)\left( {y_b^2 - y_a^2} \right)} \over 4}$ 来进行验证计算。

完整计算代码如下：

#include <iostream>
#include <cmath>

using namespace std;

void Lgwt(int n,double a,double b,double *gpt,double *gwt)
{
    int i,j,k;
    int n1,n2;
    double *xu,*y,*y0,**L,*Lp,pi,eps,temp;
    eps=1.e-8;

    pi=4.0*atan(1.0);
    n=n-1;n1=n+1;n2=n+2;

    xu=new double[n1+1];
    y=new double[n1+1];
    y0=new double[n1+1];
    L=new double*[n1+1];
    Lp=new double[n1+1];
    for(i=0;i<=n1;i++)
    {
        L[i]=new double[n2+1];
    }

    for(i=1;i<=n1;i++)
    {
        xu[i]=-1.0+(i-1)*2.0/(n1-1);
        y[i]=cos((2*(i-1)+1.0)*pi/(2*n+2))+
        (0.27/n1)*sin(pi*xu[i]*n/n2);
        y0[i]=2.0;
    }

    for(i=0;i<=n1;i++)
    {
        for(j=0;j<=n2;j++)
        {
            L[i][j]=0.0;
        }
        Lp[i]=0.0;
    }
    while(1)
    {
        temp=fabs(y[1]-y0[1]);
        for(i=2;i<=n1;i++)
        {
            if(fabs(y[i]-y0[i])>temp)
            {
                temp=fabs(y[i]-y0[i]);
            }
        }
        if(temp<1.e-12)
            break;

        for(i=1;i<=n1;i++)
        {
            L[i][1]=1.0;
            L[i][2]=y[i];
        }
        for(i=1;i<=n1;i++)
        {
            for(k=2;k<=n1;k++)
            {
                L[i][k+1]=((2*k-1)*y[i]*L[i][k]-(k-1)*L[i][k-1])/k;
            }
        }
        for(i=1;i<=n1;i++)
        {
            Lp[i]=n2*(L[i][n1]-y[i]*L[i][n2])/(1.0-y[i]*y[i]);
        }
        for(i=1;i<=n1;i++)
        {
            y0[i]=y[i];
            y[i]=y0[i]-L[i][n2]/Lp[i];
        }
    }

    for(i=1;i<=n1;i++)
    {
        gpt[i-1]=(a*(1.0-y[i])+b*(1.0+y[i]))/2.0;
        gwt[i-1]=(b-a)/((1.0-y[i]*y[i])*Lp[i]*Lp[i])*((n2*n2*1.0)/(n1*n1*1.0));
    }

    delete []xu;
    delete []y;
    delete []y0;
    delete []Lp;
    for(i=0;i<=n1;i++)
    {
        delete []L[i];
    }
    delete []L;

}

double F1(double x)
{
    //Analytical:(x2^2-x1^2)/2
    return x;
}

double F2(double x,double y)
{
    //Analytical:(x2^2-x1^2)*(y2^2-y1^2)/4
    return x*y;
}

int main()
{
    double xstart,xend,dx,x1,x2;
    double ystart,yend,dy,y1,y2;
    int xnum,ynum,i,j,ngp,ix,iy;
    double sum,analytical,err;

    double *xgpt,*xgwt,*ygpt,*ygwt;

    cout<<"Input the number of gauss points:";
    cin>>ngp;
    cout<<"Input x->[x0,xn]:";
    cin>>xstart>>xend;
    cout<<"Input y->[y0,yn]:";
    cin>>ystart>>yend;
    xnum=5;
    ynum=5;
    dx=(xend-xstart)/xnum;
    dy=(yend-ystart)/ynum;


    xgpt=new double[ngp];
    xgwt=new double[ngp];
    ygpt=new double[ngp];
    ygwt=new double[ngp];


    analytical=0.5*(xend*xend-xstart*xstart);
    sum=0.0;
    for(i=0;i<xnum;i++)
    {
        x1=xstart+i*dx;
        x2=x1+dx;
        Lgwt(ngp,x1,x2,xgpt,xgwt);
        for(j=0;j<ngp;j++)
        {
            sum+=F1(xgpt[j])*xgwt[j];
        }
    }
    cout<<"*********************************"<<endl;
    cout<<"**** One Dimension Results:  ****"<<endl;
    cout<<"**** Results:"<<sum<<endl;
    cout<<"**** Analytical Results:"<<analytical<<endl;
    cout<<"**** Error:"<<100.0*fabs(analytical-sum)/analytical<<" % "<<endl;
    cout<<"*********************************"<<endl<<endl;


    sum=0.0;
    analytical=(xend*xend-xstart*xstart)*(yend*yend-ystart*ystart)/4.0;
    for(ix=0;ix<xnum;ix++)
    {
        x1=xstart+ix*dx;
        x2=x1+dx;
        Lgwt(ngp,x1,x2,xgpt,xgwt);
        for(iy=0;iy<ynum;iy++)
        {
            y1=ystart+iy*dy;
            y2=y1+dy;
            Lgwt(ngp,y1,y2,ygpt,ygwt);
            for(i=0;i<ngp;i++)
            {
                for(j=0;j<ngp;j++)
                {
                    sum+=F2(xgpt[i],ygpt[j])*xgwt[i]*ygwt[j];
                }
            }
        }
    }
    cout<<endl<<endl;
    cout<<"*********************************"<<endl;
    cout<<"**** Two Dimension Results:  ****"<<endl;
    cout<<"**** Results:"<<sum<<endl;
    cout<<"**** Analytical Results:"<<analytical<<endl;
    cout<<"**** Error:"<<100.0*fabs(analytical-sum)/analytical<<" % "<<endl;
    cout<<"*********************************"<<endl<<endl;


    delete []xgpt;
    delete []ygpt;
    delete []xgwt;
    delete []ygwt;
    return 0;
}

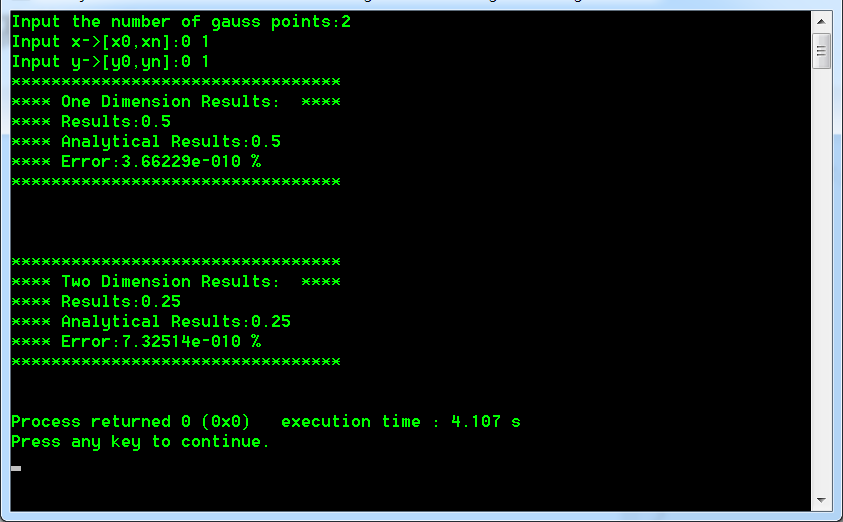
计算结果如下：
这里写图片描述

从误差对比上来看，只选取2个点的高斯积分已经很精确了！

有限元笔记1-高斯积分

猜你喜欢