参考文章:
四种方法求最长回文串
介绍一下几个概念:
回文(Pailndrome):
就是从左往右和从右往左读是一样的。就如标语“我为人人,人人为我”。
子串(substring):
子串,顾名思义,就是在原字符串中的子集,就叫子串。
串就是不能分割的,就是连在一起,这个要区别与子序列,子序列就是一段 一段的。
个人觉得这个参考文章中的代码风格值得自己学习,很多都是照搬别人的。请大家见谅。
1、暴力枚举:
枚举各个起点和终点,然后进行判断该子串是否为回文,最后就是更新最长的回文串。
枚举起点和终点 O(n^2),判断是否为回文O(n),最后复杂度为:O(n^3)
#include<bits/stdc++.h>
using namespace std;
string longestPailndrome(string &s){
int Len = s.size(); //字符串长度
int MaxLen = 1; //最长回文字符串长度
int st = 0; //最长回文字符串起始地址
for(int i = 0 ; i < Len ; i++ ){ //枚举开始位置
for(int j = i+1 ; j < Len ; j++ ){ //枚举结束位置
int tmp1=i,tmp2=j;
while( tmp1 < tmp2 && s.at(tmp1) == s.at(tmp2) ){
tmp1++; tmp2--;
}
if( tmp1 >= tmp2 && j-i+1 > MaxLen ){
MaxLen = j-i+1 ;
st=i;
}
}
}
return s.substr(st,MaxLen);
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(NULL);
string s;
cout<<"Input : \n"<<endl;
cin>>s;
cout<<"\nThe longest palindrome :\n"<<endl;
cout<<longestPailndrome(s)<<endl;
}
/*
Input:
adacbcae
The longest palindrome :
acbca
*/
运行结果:
Input:
adacbcae
The longest palindrome :
acbca2、动态规划:
设状态dp[L][R],从L开始到R这一段区域是否为回文。
明显的是:
L==R时,必回文。
L+1==R时,即相邻情况时:如果相同则说明这两端回文。
其他情况,即不再相邻时,这段回文取决于,两端点 字符相同 且 去掉两端点后会回文。
所以有:
复杂度:
因为这个只是单纯地枚举所有的两端点,其余的都是通过延伸过去得到的。
空间复杂度为O(n^2), 时间复杂度为O(n^2)
#include<bits/stdc++.h>
using namespace std;
const int N=1e2;
string longestPailndrome(string &s){
int Len = s.size(); //字符串长度
int MaxLen = 1; //最长回文字符串长度
int st = 0; //最长回文字符串起始地址
bool dp[N][N];
memset(dp,false,sizeof(dp));
for(int R=0 ; R < Len ; R++ ){
for(int L=R ; L >=0 ; L-- ){
if( R-L < 2 ){
dp[L][R]=(s[L]==s[R]);
}else{
dp[L][R]=(s[L]==s[R]&&dp[L+1][R-1]);
}
if( dp[L][R] && R-L+1 > MaxLen ){
MaxLen = R-L+1;
st=L;
}
}
}
return s.substr(st,MaxLen);
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(NULL);
string s;
cout<<"Input : \n"<<endl;
cin>>s;
cout<<"\nThe longest palindrome :\n"<<endl;
cout<<longestPailndrome(s)<<endl;
}
/*
Input:
adacbcae
The longest palindrome :
acbca
*/
运行结果:
Input:
adacbcae
The longest palindrome :
acbca3、中心扩展法:
这个中心扩展法:
其实应用的是,任意一个位置为中心,然后不断枚举两端点,只要相同即可往左右一直延伸,只要确定好奇偶性即可。
复杂度为:O(n^2),其实会比n^2更小,因为枚举过程中一旦不满足即可跳出。然后下一个中心开始。
这个比动态规划的要快,而且更加省空间。
#include<bits/stdc++.h>
using namespace std;
const int N=1e2;
string longestPailndrome(string &s){
int Len = s.size(); //字符串长度
int MaxLen = 1; //最长回文字符串长度
int st = 0; //最长回文字符串起始地址
for(int C = 0 ; C < Len ;C++ ){ //中心为C,L,R两边延伸,奇数回文
int L=C-1,R=C+1;
while( L >= 0 && R < Len && s[L]==s[R]){
if( R-L+1 > MaxLen ){
MaxLen = R-L+1;
st=L;
}
L--;R++;
}
}
for(int C= 0 ; C < Len ;C++ ){ //中心为C,L=C,偶数回文
int L=C,R=C+1;
while( L >= 0 && R < Len && s[L]==s[R]){
if( R-L+1 > MaxLen ){
MaxLen = R-L+1;
st=L;
}
L--;R++;
}
}
return s.substr(st,MaxLen);
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(NULL);
string s;
cout<<"Input : \n"<<endl;
cin>>s;
cout<<"\nThe longest palindrome :\n"<<endl;
cout<<longestPailndrome(s)<<endl;
}
/*
Input:
adacbcae
The longest palindrome :
acbca
*/
运行结果:
Input:
adacbcae
The longest palindrome :
acbca4、马拉车算法(Manacher):
推荐博客: 马拉车(Manacher)算法最通俗教学
题目练习:hiho裸题
【心路历程】:
强烈建议大家打开上面两个链接学习学习,我相信大家的水平,静下心来先把 hiho裸题中的提示全看完,然后看一下博客。真的什么叫做:“一图胜千言”,我看了两幅图,我就明白这个算法的实现了,一直都是被别人的代码带坏(以前用来套用模板做过一道题,但是那个代码很丑陋感觉就很难理解),一直以为很难很难,其实真的看懂之后我就觉得没有什么大不了。现在看完了,看懂了,感觉很好,很好 ^_^
回文串的特点:左右对称。
比如说,有一个字符串S为:*)~AxbxExbxA#%&
观察看出来了:最长回文子串当然是 以'E'为中心,长度为9的最长回文子串。
推论:
假如:在我们得到这个 “以'E'为中心,长度为9的最长回文子串”后
我们找到了在其中有一局部同样是 回文串,如A“xbx”ExbxA,
可以断言:在此 以E为中心的另一侧 同样存在相同的回文串:AxbxE“xbx”A
根据这一个推论我们就可以进行推导了:
我们现在手头上只具备,字符串S ,和刚才的一个推论。
还没有什么好的想法:
但是通过推论我们知道,必须知道 “某一位置上的最长回文长度”才进行推导。
大体思路:
我们需要设立一个数组,用于存储“某一位置上的最长回文长度”(用Len[ ]数组存储)。然后进行的操作是:对于每一位上的i( 1<=i<=len (S) )。然后每一位上我们需要一些辅助的变量,记录当前最长的位置到了哪里(即最右端:D)?并且这个最长的位置是哪一个位置为中心所得到的(即产生最右端的中心点:P)。在访问当前的位置时,只要是在最右端内,我们都可以以P为中心在前半段位置中找出对应的长度。一直往右更新即可。大家直接看Manacher的具体实现吧!!!
以下内容都是在仿造推荐博客上的。其中图都是从中偷来的,请大家谅解。
Manacher原理及其算法实现:
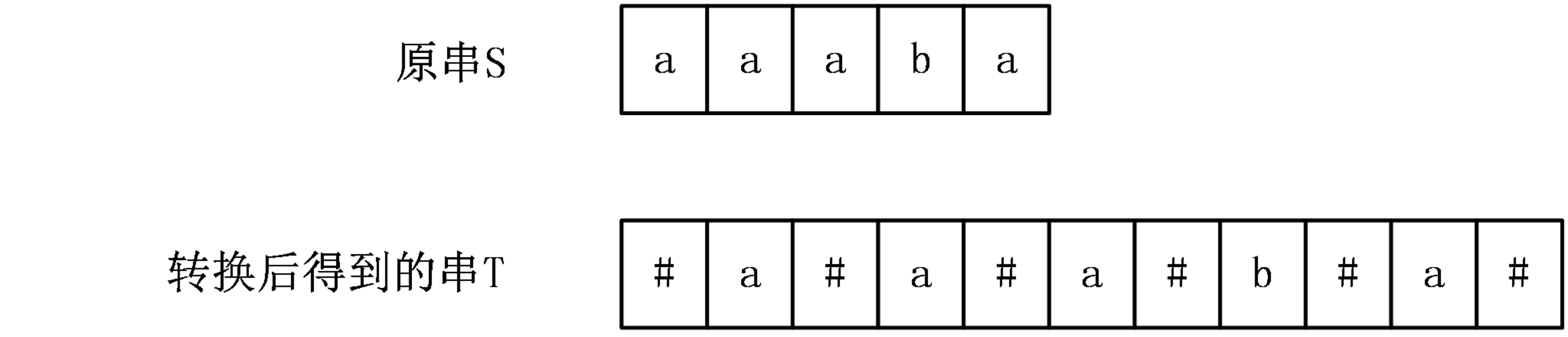
一、预处理:
观察一下:这样处理的好处是什么???
因为回文串是有奇偶性之分,类似与"ABBA",“ABA”。
偶数:对称轴是"AB | BA"
奇数:对称轴是“A ‘B' A”
偶数处理过后:“#A#B#B#A#”,我们的对称轴是“#A#B#B#A#”
奇数处理过后:“#A#B#A#” ,我们的对称轴是 “#A#B#A#”
这样处理过后可以把偶数中对称轴 为空隙的情况解决了。我们只要讨论转化后的T串,每一个位置上为中心都是尤其道理的。
二、辅助数组Len的简介与性质:
1、Len数组是什么?
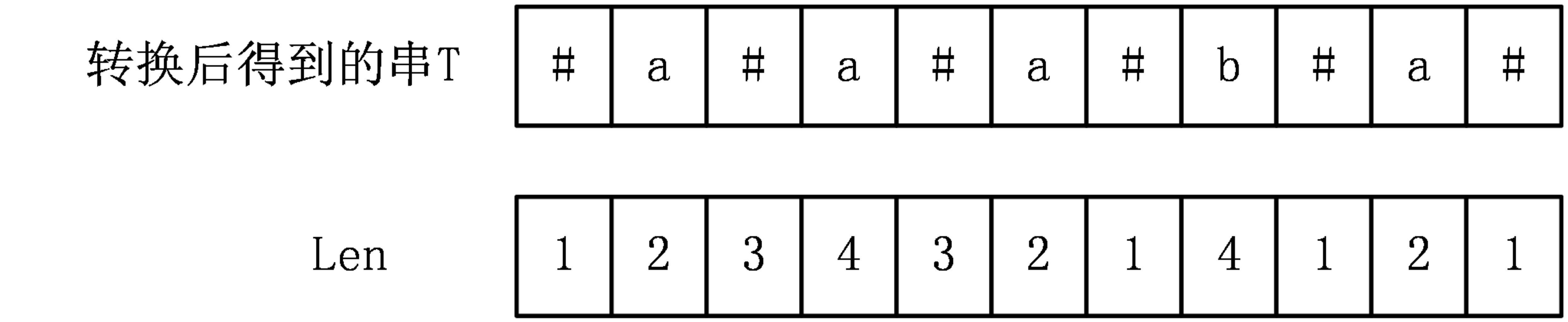
Manacher算法用一个辅助数组Len[i]表示以字符T[i]为中心的最长回文字串的最右字符到T[i]的长度(长度指的是中心到右端点的距离,两个端点都包括),比如以T[i]为中心的最长回文字串是T[l,r],那么Len[i]=r-i+1。如“#A#”,Len[ 2 ] = 2, 中心点"A" -> 右端点"#",包括了两个端点的位置,所以是Len[2]=3-2+1=2.
对于上面的例子,可以得出Len[i]数组为:
2、Len数组性质:
Len[i]-1 : 表示原字符串中S,在i位置上最长回文子串。(i为偶数时,表明的是以S[i]该字符为对称轴,i为奇数时,表明是以S[i],S[i+1]两个字符之间的空隙)
证明:
为了更好地表示最长回文子串(Longest Palindrome String)简写(LPS)
对于转化为字符串T后,所有的回文子串都转化为计算奇数回文子串的方法。(预处理中提到了,奇数是以字符为对称轴,偶数是以字符间的空隙为对称轴,当转化为T字符串后,空隙即为“#”)
计算当前在字符串T中,i为中心的最长回文子串长度(LPS)为:2*len[ i ] -1
∵在转化为T串时,分隔符“#”,总是会比原来的S串要多。
∴分隔符必定为Len[i]个
∴转化为S串后,这个答案就是 S串LPS=T串LPS-分隔符。
∴LPS=(2×Len[ i ] -1 )- Len [ i ]=Len [ i ] -1
到了这一步,我们要算一个原来的字符串S 的LPS,转化为更新Len数组的值。
3、Len数组的计算
主要还是参考博客:马拉车(Manacher)算法最通俗教学
首先从左往右依次计算Len[i],当计算Len[i]时,Len[j](0<=j<i)已经计算完毕。设P为之前计算中最长回文子串的右端点的最大值,并且设取得这个最大值的位置为po,分两种情况:
第一种情况:i<=P:
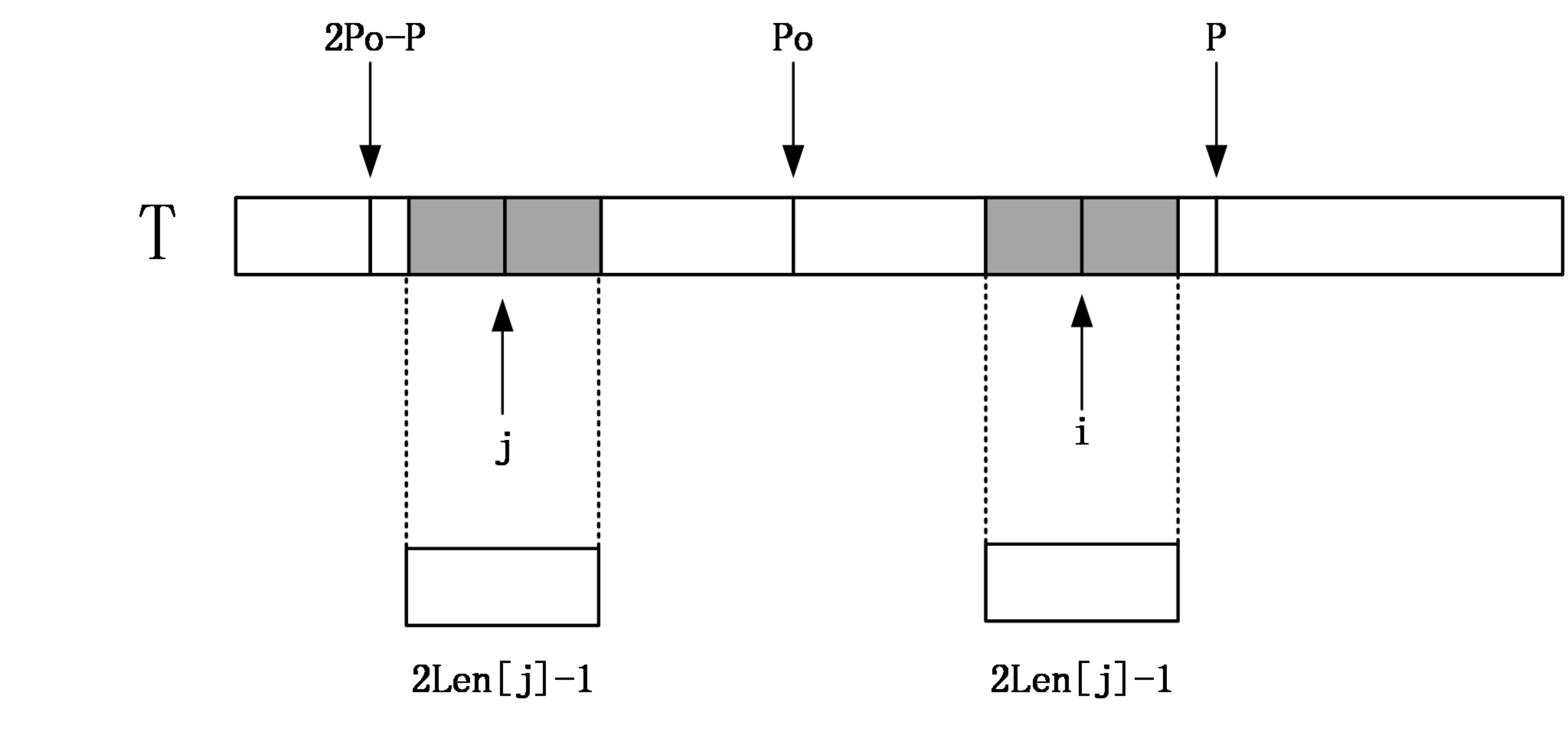
那么找到i相对于po的对称位置,设为j,那么如果Len[j]<P-i,如下图:
看图我们都清楚了,我们在讨论 i 位置时,Len[ i ] >= Len [ j ],为什么是大于等于呢?
∵我们不清楚P向外延伸的是否还是回文?
∴我们需要再进一步向外延伸,所以就有下面的图和解释了。
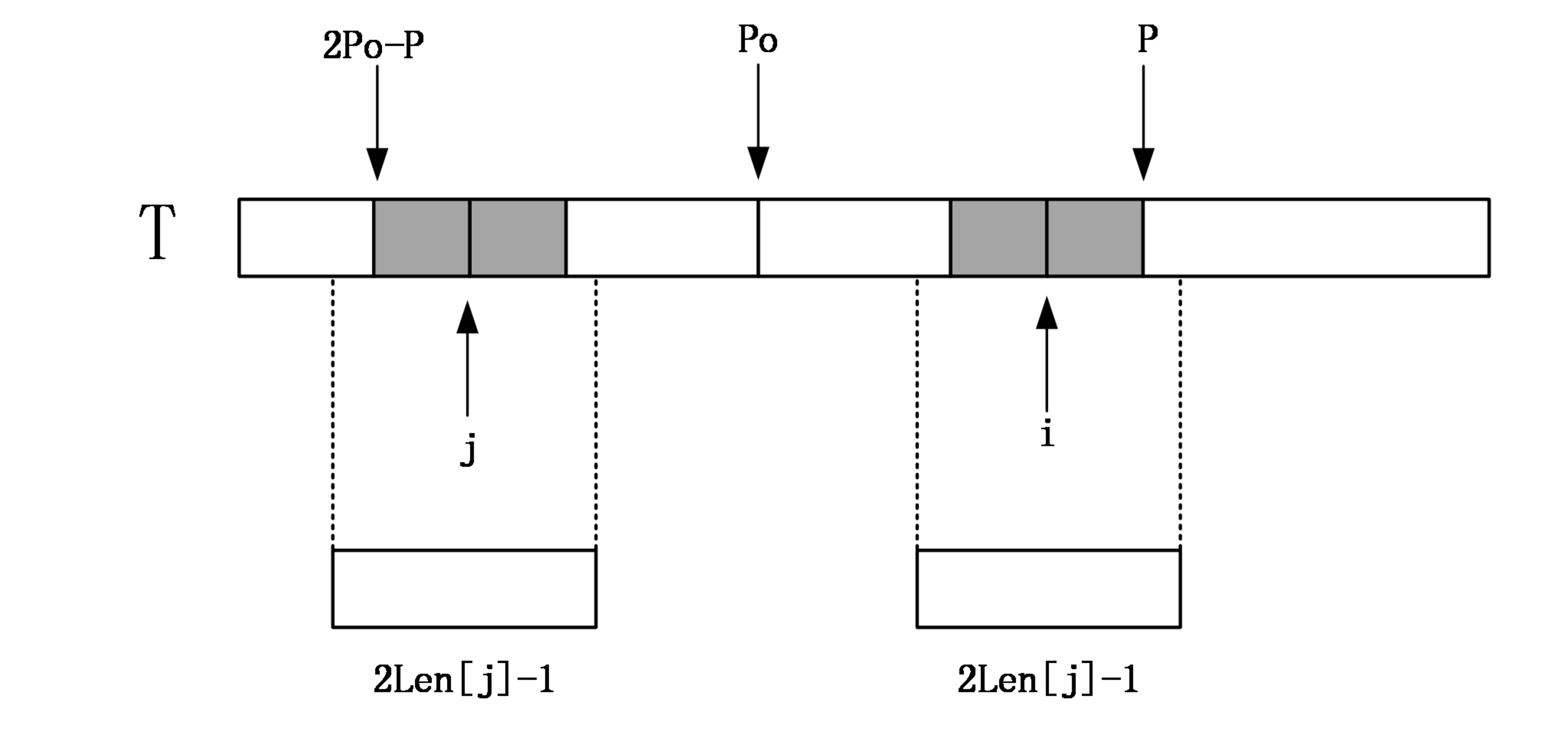
如果Len[j]>=P-i,由对称性,说明以i为中心的回文串可能会延伸到P之外,而大于P的部分我们还没有进行匹配,所以要从P+1位置开始一个一个进行匹配,直到发生失配,从而更新P和对应的po以及Len[i]。
第二种情况: i>P
如果i比P还要大,说明对于中点为i的回文串还一点都没有匹配,这个时候,就只能老老实实地一个一个匹配了,匹配完成后要更新P的位置和对应的po以及Len[i]。
4、时间复杂度分析
Manacher算法的时间复杂度分析和Z算法类似,因为算法只有遇到还没有匹配的位置时才进行匹配,已经匹配过的位置不再进行匹配,所以对于T字符串中的每一个位置,只进行一次匹配,所以Manacher算法的总体时间复杂度为O(n),其中n为T字符串的长度,由于T的长度事实上是S的两倍,所以时间复杂度依然是线性的。
下面是算法的实现,注意,为了避免更新P的时候导致越界,我们在字符串T的前增加一个特殊字符,比如说‘$’,所以算法中字符串是从1开始的。
大家知道怎么一回事了,就开始自己写写代码看看自己是否真正掌握了。
hiho裸题
自己写的模板:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
char S[N],T[N<<1];
int Len[N<<1];
int Manacher(char *s){
int L=strlen(s),po=0,mx=0,lps=1;
for(int i=1;i<=L*2;i++){
T[i]=i&1?'#':s[i/2-1];
}
T[0]='@';
T[2*L+1]='#';
T[2*L+2]='\0';
for(int i=1;i<=2*L;i++){
if( i<mx )
Len[i]=min(mx-i,Len[2*po-i]);
else
Len[i]=1;
while(T[i+Len[i]]==T[i-Len[i]])
Len[i]++;
if(i+Len[i]>mx){
po=i;
mx=i+Len[i];
}
lps=max(lps,Len[i]-1);
}
return lps;
}
int main()
{
int T,LPS;
scanf("%d",&T);
while(T--){
scanf("%s",S);
LPS=Manacher(S);
printf("%d\n",LPS);
}
return 0;
}