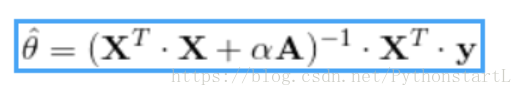线性回归的小trick

线性回归

感觉线性回归当中讲的东西不太多，前提是不涉及贝叶斯的情况，关于贝叶斯相关的回归，可以学习一下bishop的PRML（模式识别与机器学习），之前我在学习统计相关的课程的时候也接触过一点。。。记得lasso、岭回归什么的都是贝叶斯线性回归的退化情况。

普通的广义线性模型，都是拟合一个带有系数 $w = (w_1, ..., w_p)$ 的线性模型，使得数据集实际观测数据和预测数据（估计值）之间的残差平方和最小。其数学表达式为：

$\underset{w}{min\,} {|| X w - y||_2}^2$ ，当然如果是做分类的话，请参照李航的logistic回归、后面的博客我在仔细说一下关于logistics回归与softmax回归。后面得到系数

这篇博客主要介绍岭回归、lasso、弹性网络回归三种线性回归加正则项的方式并比较一下。事实上降低模型的过拟合的好方法是正则化这个模型（即限制它）：模型有越少的自由度，就越难以拟合数据。例如，正则化一个多项式模型，一个简单的方法就是减少多项式的阶数。

对于一个线性模型，正则化的典型实现就是约束模型中参数的权重。接下来我们将介绍三种不同约束权重的方法：Ridge 回归，Lasso 回归和 Elastic Net。

岭回归

岭回归通过对系数的大小施加惩罚来解决普通最小二乘法的一些问题。岭系数最小化的是带罚项的残差平方和，

$\underset{w}{min\,} {{|| X w - y||_2}^2 + \alpha {||w||_2}^2}$

岭回归（也称为 Tikhonov 正则化）是线性回归的正则化版：在损失函数上直接加上一个正则项这使得学习算法不仅能够拟合数据，而且能够使模型的参数权重尽量的小。注意到这个正则项只有在训练过程中才会被加到损失函数。当得到完成训练的模型后，我们应该使用没有正则化的测量方法去评价模型的表现。

和普通OLS估计相比

对于普通最小二乘的系数估计问题，其依赖于模型各项的相互独立性。当各项是相关的，且设计矩阵 $X$ 的各列近似线性相关，那么，设计矩阵会趋向于奇异矩阵，这会导致最小二乘估计对于随机误差非常敏感，产生很大的方差。例如，在没有实验设计的情况下收集到的数据，这种多重共线性（multicollinearity）的情况可能真的会出现，这就导致求的时候，逆矩阵无法计算或者只能用伪逆进行代替

伪逆矩阵是逆矩阵的广义形式。由于奇异矩阵或非方阵的矩阵不存在逆矩阵，但在matlab里可以用函数pinv(A)求其伪逆矩阵。基本语法为X=pinv(A),X=pinv(A,tol),其中tol为误差,pinv为pseudo-inverse的缩写：max(size(A))*norm(A)*eps。函数返回一个与A的转置矩阵A' 同型的矩阵X，并且满足：AXA=A,XAX=X.此时，称矩阵X为矩阵A的伪逆，也称为广义逆矩阵。pinv(A)具有inv(A)的部分特性，但不与inv(A)完全等同。　如果A为非奇异方阵，pinv(A)=inv(A)，但却会耗费大量的计算时间，相比较而言，inv(A)花费更少的时间

一般这时候我们会用lasso或者岭回归的方法进行代替，lasso可以很好的克服没有逆矩阵的缺点，只要你把参数的alpha设置的足够大，总能得到逆矩阵

下面岭回归的封闭方程的解

损失函数和评价函数

一般情况下，训练过程使用的损失函数和测试过程使用的评价函数是不一样的。除了正则化，还有一个不同：训练时的损失函数应该在优化过程中易于求导，而在测试过程中，评价函数更应该接近最后的客观表现。一个好的例子：在分类训练中我们使用对数损失（以后我们会写博客讨论他）作为损失函数，但是我们却使用精确率/召回率来作为它的评价函数。

如果是Square loss，那就是最小二乘了；

如果是Hinge Loss，那就是著名的SVM了；

如果是exp-Loss，那就是牛逼的 Boosting了；

如果是log-Loss，那就是Logistic Regression了

在sklearn中我们这样使用岭回归

from sklearn import linear_model
lingreg = linear_model.Ridge()
lingreg.fit(housing_prepared,housing_labels)
lingreg.predict(some_data)

关于参数的设置

RidgeCV 通过内置的 Alpha 参数的交叉验证来实现岭回归。该对象与 GridSearchCV 的使用方法相同，只是它默认为 Generalized Cross-Validation(广义交叉验证 GCV)，这是一种有效的留一验证方法（LOO-CV）下图是sklearn的官方api介绍

Lasso 回归

Lasso 回归（也称 Least Absolute Shrinkage，或者 Selection Operator Regression）是另一种正则化版的线性回归：就像岭回归那样，它也在损失函数上添加了一个正则化项，但是它使用权重向量的 L1 范数而不是权重向量 L2范数平方的一半。

Lasso 回归的损失函数

Lasso 回归的一个重要特征是它倾向于完全消除最不重要的特征的权重（即将它们设置为零）

Lasso是一个特别有用的线性回归，他具有稀疏性，可以帮助我们进行选择，会使很多不重要的特征变量的权重为0，为什么这么做呢，是因为如图所示，L1正则化项是左上角这种菱形，所依在高维空间中有很多在该权重处不可导的地方，可以看到右上图，当θ2 一直在0的位置徘徊。而右下当取L2正则化项时，t可以一直往下进行梯度下降。

代码如下

from sklearn import linear_model
lingreg = linear_model.Lasso(alpha=0.1)
lingreg.fit(housing_prepared,housing_labels)
lingreg.predict(some_data)

弹性网络回归

弹性网络介于 Ridge 回归和 Lasso 回归之间。它的正则项是 Ridge 回归和 Lasso 回归正则项的简单混合，同时你可以控制它们的混合率 r，当 r=0时，弹性网络就是 Ridge 回归，当 r= 1时，其就是 Lasso 回归

from sklearn.linear_model import ElasticNet
lingreg = ElasticNet(alpha=0.1,l1_ratio=0.5)
lingreg.fit(housing_prepared,housing_labels)
lingreg.predict(some_data)

我们该如何选择线性回归，岭回归，Lasso 回归，弹性网络呢？

一般来说有一点正则项的表现更好，因此通常你应该避免使用简单的线性回归。岭回归是一个很好的首选项，但是如果你的特征仅有少数是真正有用的，你应该选择 Lasso 和弹性网络。就像我们讨论的那样，它两能够将无用特征的权重降为零。一般来说，弹性网络的表现要比 Lasso 好，因为当特征数量比样本的数量大的时候，或者特征之间有很强的相关性时，Lasso 可能会表现的不规律

此篇博客参考了https://blog.csdn.net/sinat_26917383/article/details/52092040