[Python3 练习] 006 汉诺塔2 非递归解法

题目：汉诺塔 II

• 接上一篇 [Python3 练习] 005 汉诺塔1 递归解法
• 这次不使用递归
• 不限定层数

(1) 解决方式

• 利用“二进制”

(2) 具体说明

• 统一起见
  • 我把左、中、右三根针依次称为 A 塔、B 塔、C 塔
  • 金片默认都在 A 塔
  • n 片金片从小到大依次编号为 0 号、1 号、……、n-1 号

1) 举个“栗子”

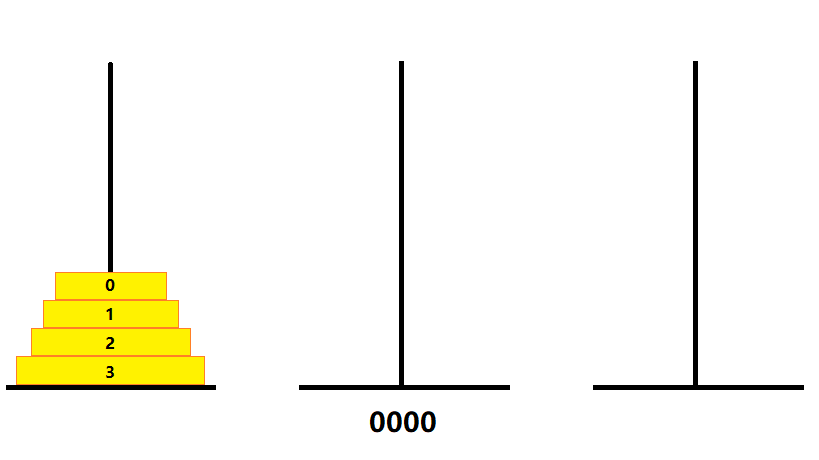
• 假设有一个 4 层高的汉诺塔，设初始值为 0000₍₂₎
• 按 “8”、“4”、“2”、“1” 称呼二进制的各位，“8”、“4”、“2”、“1” 依次对应 3 号金片、2 号金片、1号金片、0 号金片
• 如图
  

---

• 开始累加，每次加 1
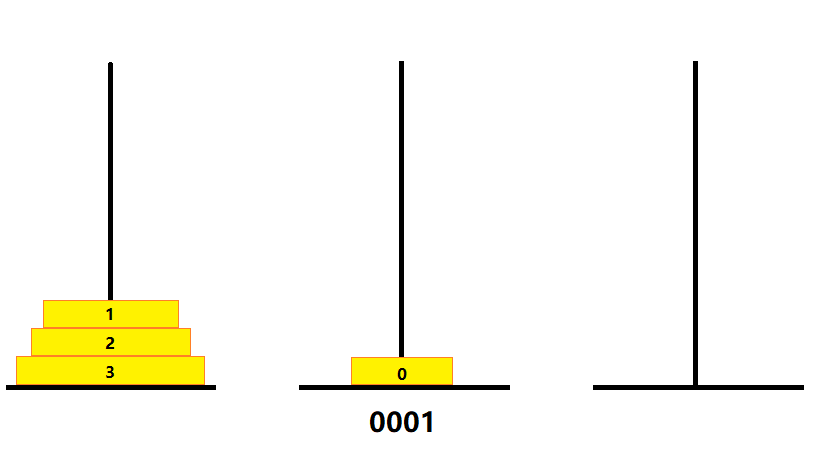
• 0001₍₂₎
• 个位由 0 变 1，则将 0 号金片向右移一格，即将 0 号金片移至 B 塔
  • 若要将 C 塔上的金片右移，则做一个循环，即移至 A 塔
• 如图
  

---

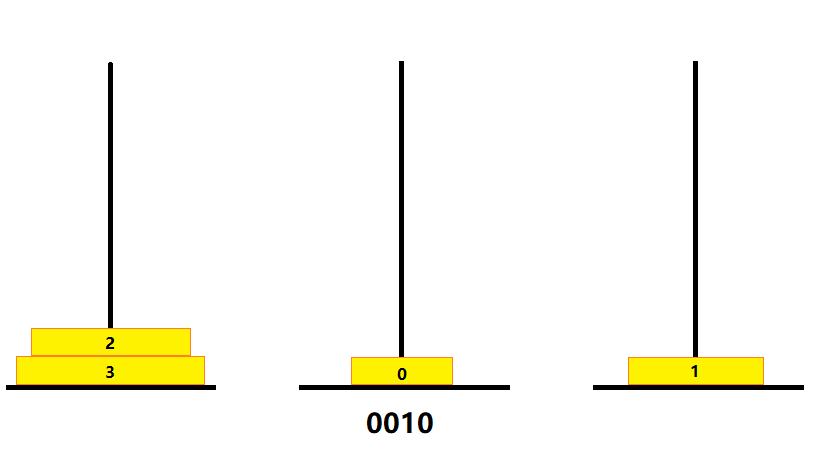
• 0010₍₂₎
• 产生进位，进到哪位，则移动该位对应的金片
• 此时进位至“2”位，则将 1 号金片右移，因为 1 号金片不能放在 B 塔的 0 号金片上方，所以只能将其放到空无一物的 C 塔上
• 如图
  

---

• 0011₍₂₎
• 个位由 0 变 1，则将 B 塔的 0 号金片移至 C 塔
• 如图
  

---

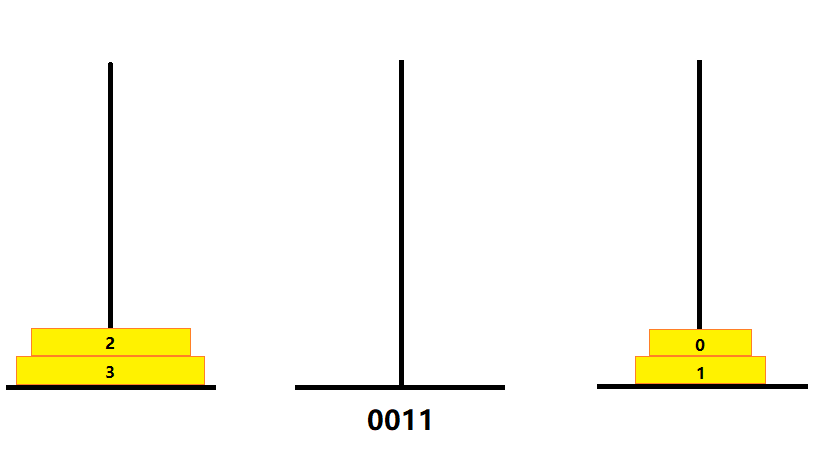
• 0100₍₂₎
• 产生进位，此时进至“4”位，则 2 号金片移至 B 塔
• 如图
  

---

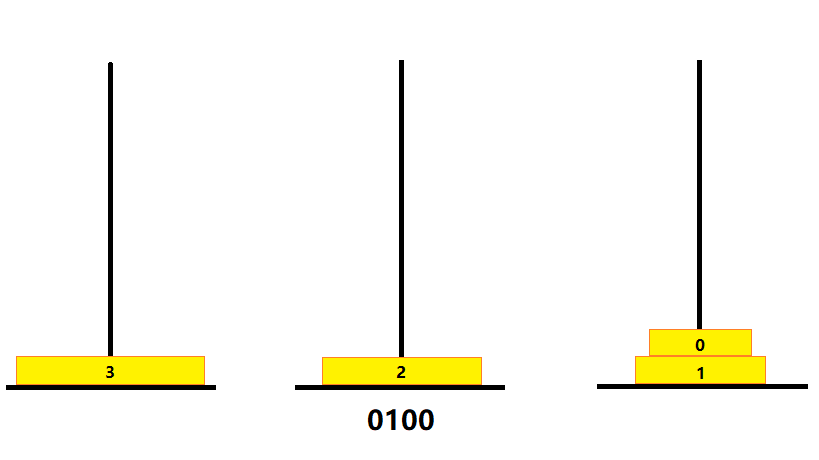
• 0101₍₂₎
• 个位由 0 变 1，则将 C 塔的 0 号金片移至 A 塔
• 如图
  

……

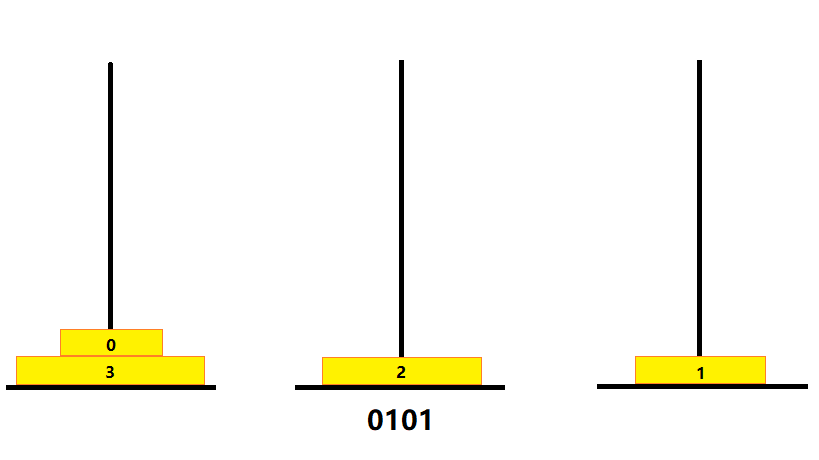
• 按这个方法进行下去，最终能将 A 塔的 4 片金片都移至 C 塔

2) 一些说明

• 此“二进制”方法可以解决汉诺塔，但奇数金片与偶数金片在结果上有些许不同
  • 按照上面的规则，奇数金片最终会移至 B 塔，偶数金片最终会移至 C 塔
  • 可借高数中“轮换对称性”的思想，在面对奇数金片时，把原来的 B 塔看成 C 塔，把原来的 C 塔看成 B 塔
• 上面的操作有 2 个规律
  • 规律一
    • 因为每走一步，数值加 1，所以该二进制数即为步数
    • 该二进制数从右往左数 0，遇到第一个 1 停止计数，0 的个数与此步要移动的金片的编号一样
    • 没有 0，即为 0 个 0，对应 0 号金片；1 个 0，对应 1 号金片……依此类推
  • 规律二
    • 编号为 0、2、4……的金片，总是进行右移操作
    • 编号为 1、3、5……的金片，总是进行左移操作

3) 计算移动次数

• 按递归的思路，汉诺塔可分成三大步
  • 将 A 塔的上面 n-1 片金片移至 B 塔
  • 将 A 塔剩余的 1 片金片移至 C 塔
  • 将 B 塔的 n-1 片金片移至 C 塔
• 设 f(n) 为 n 片金片完成移动需要的最少次数，则 f(n) = f(n-1) + 1 + f(n-1)，即 f(n) = 2f(n-1) + 1
  • 若只有 1 片金片，则 f(1) = 1
  • 若有 2 片金片，则 f(2) = 3
  • 若有 3 片金片，则 f(3) = 7
  • 照此规律，可假设 f(n) = 2ⁿ - 1
• 莫名想到线代中用的“第一类数学归纳法”，我献丑证一下，算是温故知新
  • 证明 f(n) = 2ⁿ - 1 成立：
  • 当 n = 1 时，f(1) = 2¹ - 1 = 1，成立
  • 当 n = k 时，设 f(k) = 2^k - 1 成立
  • => 当 n = k + 1 时，f(k+1) = 2f(k) + 1 = 2 * (2^k - 1) + 1 = 2^k+1 - 1，满足假设
  • => 汉诺塔的移动次数为 f(n) = 2ⁿ - 1，证毕

(3) 程序

1) 代码

# 不使用递归

def hanoi(n):
    tower_belong = [0] * n  # 用列表开辟 n 个空间，用于存放 n 个金片各自的编号，编号对应塔号
                            # 金片移动，编号对应更改
    if n % 2 == 0:          # 金片的编号对应这里的塔号
        tower_name = ['A', 'B', 'C']    # 若 n 为偶数，最终所有金片恰好能移到 C 塔
    else:
        tower_name = ['A', 'C', 'B']    # 若 n 为奇数，最终所有金片会移到 B 塔
                                        # 用“轮换对称”将 B、C 两塔互换名字，以实现“负负得正”
    for step in range(1, 2**n):         # n 片金片最少需要移动 2^n - 1 次
        bin_step = bin(step)            # 求得 step 的二进制数值
        gold_num = len(bin_step) - bin_step.rfind('1') - 1
        # 计算 step 末尾 0 的个数，得到金片编号
        # 如 step = 0b0001，则 step 末尾 0 的个数为 0，表示此刻应移动 0 号金片
        # 如 step = 0b0100，则 step 末尾 0 的个数为 2，表示此刻应移动 2 号金片，依此类推
        
        print('第', str(step), '步：移动', str(gold_num), '号塔，从', \
              tower_name[tower_belong[gold_num]], '到', end=' ') # 移出金片的塔
        if gold_num % 2 == 0:                                   # 若 num 为 偶数，则右移
            tower_belong[gold_num] = (tower_belong[gold_num] + 1) % 3
            # 若从 C 塔右移，则又回到了 A 塔
        else:                                                   # 若 num 为奇数，则左移
            tower_belong[gold_num] = (tower_belong[gold_num] + 2) % 3
            # 若从 A 塔左移，则又去到了 C 塔
        print(tower_name[tower_belong[gold_num]])               # 移入金片的塔

2) 运行情况

• 3 层汉诺塔
  

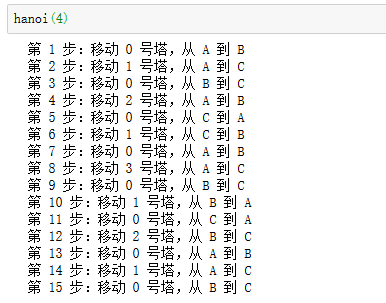
• 4 层汉诺塔