Nowadays, I learnt from Liu Ben a question asked in the interview of ENS.
Assume $m,n$ are two coprime odd numbers, consider the inteval $[0,mn]$. We cut the inteval by $m,2m,\ldots,(n-1)m$ and $n, 2n,\ldots, (m-1)n$ into $m+n+1$ pieces of small intevals. And we color them from left to right by black-and-white periodically and black first. The question is to show $$(\textrm{the length of black})-(\textrm{the length of white})=1$$
For example, if $m=3,n=5$, $$\begin{array}{c*{31}}0 &&&&&& 3 &&&&&& 6 &&&&&& 9 &&&&&& 12 &&&&&& 15 \\ \mid & \blacksquare && \blacksquare && \blacksquare &\mid & \square && \square & \mid & \blacksquare & \mid & \square&& \square&& \square &\mid & \blacksquare &\mid & \square&& \square&\mid & \blacksquare&& \blacksquare&& \blacksquare & \mid \\ 0 &&&&&&&&&& 5 &&&&&&&&&& 10 &&&&&&&&&& 15\end{array} $$The length of black is $8$ and the length of white is $7$.

The problem seems to be elementary at the first sight. But after a period of thinking, one find it is hard to deal with. Here is Liu Ben's Original answer, I fulfill details to read more easily,
The number of cuts before $x$ is $\lfloor \frac{x-1}{n}\rfloor+\lfloor \frac{x-1}{m}\rfloor$, so $$(-1)^{\lfloor \frac{x-1}{n}\rfloor+\lfloor \frac{x-1}{m}\rfloor}=\begin{cases} 1 & \textrm{$[x-1,x]$ is colored by black }\\ -1 & \textrm{$[x-1,x]$ is colored by white } \end{cases}$$Thus it is equivlent to show that $\sum_{x=0}^{mn-1} (-1)^{\lfloor \frac{x}{n}\rfloor+\lfloor \frac{x}{m}\rfloor}=1$, and we have know that $(-1)^{m+n}=1, (-1)^0=1$, so it is equivlent to show that $$\sum_{x=1}^{mn} (-1)^{\lfloor \frac{x}{n}\rfloor+\lfloor \frac{x}{m}\rfloor}=1$$Now we need some identity to expand the expression $(-1)^{\lfloor \frac{x}{n}\rfloor}$,
$$\begin{array}{rll} (-1)^{\lfloor x \rfloor}& = (-1)^{\lfloor x\rfloor}-1+1 \\ & =1+ 2\left(\sum_{n=0}^{\lfloor x\rfloor}(-1)^{n}\right)= 1+ 2\left(\sum_{n\leq x}(-1)^{n}\right)\end{array}$$
So
$$\begin{array}{rll}&\quad \sum_{x=1}^{mn} (-1)^{\lfloor \frac{x}{n}\rfloor+\lfloor \frac{x}{m}\rfloor} \\ & =\sum_{x=1}^{mn} \left(1+2\left(\sum_{k\leq x/n} (-1)^k \right)\right)\left(1+2\left(\sum_{k\leq x/m} (-1)^k\right)\right) \\ & = mn+2\underbrace{\sum_{x=1}^{mn}\sum_{k\leq x/n} (-1)^k}_{:=A}+2\underbrace{\sum_{x=1}^{mn}\sum_{k\leq x/m} (-1)^k}_{:=B}+4\sum_{x=1}^{mn}\left(\sum_{k\leq x/n} (-1)^k\right)\left(\sum_{h\leq x/m} (-1)^h\right)\end{array}$$
Firstly, we calculate $A$,
$$\begin{array}{rll}A & =\sum_{x=1}^{mn}\sum_{k\leq x/n} (-1)^k \\ & = \sum_{k=1}^m \#\{x\geq nk: x=1,\ldots,mn\}(-1)^k \\ & =\sum_{k=0}^m n(m-k)(-1)^k \\ & = n\sum_{k=0}^m k(-1)^k\\& =-n\frac{m+1}{2}\end{array}$$
Similarly, $B=-m\frac{n+1}{2}$, therefore it remains to show
$$\sum_{x=1}^{mn}\left(\sum_{k\leq x/n} (-1)^k\right)\left(\sum_{h\leq x/m} (-1)^h\right)=\frac{(m+1)(n+1)}{4}$$
Let's compute !
$$\begin{array}{rll}\sum_{x=1}^{mn}\left(\sum_{k\leq x/n} (-1)^k\right)\left(\sum_{h\leq x/m} (-1)^h\right) & =\sum_{k=0}^{m}\sum_{h=0}^n\#\{x\geq \max (nk,mh), x=1,\ldots,mn\}(-1)^{k+h}\\ & =\sum_{k=0}^{m}\sum_{h=0}^n(mn- \max(nk,mh))(-1)^{k+h} \\ & =\sum_{k=0}^{m}\sum_{h=0}^n \max(nk,mh)(-1)^{k+h} \\ & =\sum_{k=0}^{m}\sum_{h=0}^n \frac{1}{2}(nk+mh+\left|nk-mh\right|)(-1)^{k+h} \\ &= \frac{1}{2}\sum_{k=0}^{m}\sum_{h=0}^n \left|nk-mh\right|(-1)^{k+h} \\ & = \frac{mn}{2}\sum_{k=0}^m\sum_{h=0}^n\left|\frac{k}{m}-\frac{h}{n}\right|(-1)^{k+h}\end{array}$$
So it reduces to show $\sum_{k=0}^m\sum_{h=0}^n\left|\frac{k}{m}-\frac{h}{n}\right|(-1)^{k+h}=0$. We need some tools to calculate, consider the function $f$ with peroid $2$ and $f(x)=|x|$ for $x\in [-1,1]$, then the Fourier series of $f$ is $$f=\sum_{\ell \in \mathbb{Z}} a_{\ell} \mathrm{e}^{\frac{2\pi i \ell x}{2}}\qquad a_{\ell} =\frac{1}{2}\int_{-1}^1 |x| \mathrm{e}^{\frac{2\pi i \ell x}{2}}\textrm{d}x=\begin{cases}\frac{1}{2} & n=0 \\ -\frac{2}{\pi^2 n^2} & n\textrm{is odd} \\ 0 & n\neq 0\textrm{is even}\end{cases}$$
In other word, we have
$$x\in [-1,1]\Rightarrow \frac{1}{4}-\frac{|x|}{2}=\sum_{\ell \textrm{odd}} \frac{1}{\pi^2 \ell ^2}\mathrm{e}^{2\pi i \ell x}$$
Now, continuous
$$\begin{array}{rll} \frac{mn}{2}\sum_{k=0}^m\sum_{h=0}^n\left|\frac{k}{m}-\frac{h}{n}\right|(-1)^{k+h} & = mn \sum_{k=0}^m\sum_{h=0}^n\frac{\left|\frac{k}{m}-\frac{h}{n}\right|}{2}(-1)^{k+h} \\ & =mn \sum_{k=0}^m\sum_{h=0}^n\bigg(\frac{1}{4}-\frac{\left|\frac{k}{m}-\frac{h}{n}\right|(-1)^{k+h}}{2} \bigg) \\ & = \sum_{k=0}^m \sum_{h=0}^n \sum_{\ell\textrm{odd}} \frac{1}{\pi^2 \ell ^2} \mathrm{e}^{\frac{2\pi i}{2}\cdot \ell \left(\frac{k}{m}-\frac{h}{n}\right)} \\ & =mn\sum_{\ell \textrm{odd}} \frac{1}{\pi^2 \ell^2 }\left(\sum_{k=0}^m (-1)^k\mathrm{e}^{\frac{2 \pi i \ell k}{2 m }}\right)\left(\sum_{h=0}^n (-1)^h\mathrm{e}^{-\frac{2 \pi i \ell h}{2 n }}\right)\end{array}$$
It reduces to the case of the summation of geometry series, we have
$$\sum_{k=0}^m (-1)^k\mathrm{e}^{\frac{2 \pi i \ell k}{2 m }}=\begin{cases}-1& m\nmid \ell \\ -1+m & m\mid \ell \end{cases}\qquad \sum_{h=0}^n (-1)^h\mathrm{e}^{-\frac{2 \pi i \ell h}{2 n }} = \begin{cases}-1& n\nmid \ell \\ -1+n & n\mid \ell \end{cases}$$
Now we can deduct the result,
$$\begin{array}{rll} & \quad mn\sum_{\ell \textrm{odd}} \frac{1}{\pi^2 \ell^2 }\left(\sum_{k=0}^m (-1)^k\mathrm{e}^{\frac{2 \pi i \ell k}{2 m }}\right)\left(\sum_{h=0}^n (-1)^h\mathrm{e}^{-\frac{2 \pi i \ell h}{2 n }}\right) \\ & =mn\sum_{\ell \textrm{odd}} \frac{1}{\pi^2 \ell^2 } - mn\sum_{\begin{subarray}{l}\ell \textrm{odd}\\ m|\ell \end{subarray}} \frac{m}{\pi^2 \ell^2} - mn\sum_{\begin{subarray}{l}\ell \textrm{odd}\\ n|\ell \end{subarray}} \frac{n}{\pi^2 \ell^2} + mn\sum_{\begin{subarray}{l}\ell \textrm{odd}\\ n|\ell \\ m|\ell \end{subarray}} \frac{nm}{\pi^2 \ell^2} \\ & = mn\sum_{\ell \textrm{odd}} \frac{1}{\pi^2 \ell^2 } - n\sum_{\begin{subarray}{l}\ell \textrm{odd}\\ m|\ell \end{subarray}} \frac{1}{\pi^2 (\ell/m)^2} - m\sum_{\begin{subarray}{l}\ell \textrm{odd}\\ n|\ell \end{subarray}} \frac{1}{\pi^2 (\ell/n)^2} + \sum_{\begin{subarray}{l}\ell \textrm{odd}\\ nm\mid \ell \end{subarray}} \frac{1}{\pi^2 (\ell/mn)^2} \\ & =(m-1)(n-1) \sum_{\ell \textrm{odd}} \frac{1}{\pi^2 \ell^2 } =\frac{(m-1)(n-1)}{4}\end{array}$$
The proof is complete. $\square$
If we reflect the process above carefully, we will find that the trick of exponential sums is useful in the domain of combinatorics involving number theory. It is powerful but not too beutiful. The amazing point is that in the process of counting number, $\pi$ can occur, even it will be cancelled finally.
Some days after, Liu Ben gives a new answer which uses Fourier analysis, it is more elegant than the above, and I fulfill details to read more easily,
Actually, as above it reduces to show $$\int_0^{mn}(-1)^{\lfloor \frac{x}{n}\rfloor+\lfloor \frac{x}{m}\rfloor}\textrm{d}x=\int_0^{mn}(-1)^{\lfloor \frac{x}{n}\rfloor}\overline{(-1)^{\lfloor \frac{x}{m}\rfloor}}\textrm{d}x=1$$Conside $f(x)=(-1)^{\lfloor x\rfloor}$ as a function of period $2$, one can calculate its Fourier expansion$$f(x)=\frac{2}{\pi i}\sum_{\ell\textrm{odd}}\frac{1}{\ell} \mathrm{e}^{\frac{2\pi i \ell x}{2}}$$So $$\begin{array}{rll}\int_0^{mn}(-1)^{\lfloor \frac{x}{n}\rfloor}\overline{(-1)^{\lfloor \frac{x}{m}\rfloor}}\textrm{d}x& =\int_{0}^{mn}f(nx)\overline{f(mx)}\textrm{d}x \\ & =mn\int_0^1 f(y/n)\overline{f(y/n)}\textrm{d}y \\ & = \frac{4 mn}{\pi^2}\sum_{\begin{subarray}{l}r,s \textrm{odd} \\ mr=ns\end{subarray}}\frac{1}{rs} \\ & = \frac{4 mn}{\pi^2}\sum_{\begin{subarray}{l}r,s \textrm{odd} \\ r=tn,s=tm\end{subarray}}\frac{1}{rs} \\ & =\frac{4}{\pi^2}\sum_{t\textrm{odd}}\frac{1}{t^2}=1\end{array} $$The proof is complete. $\square$
To complete this post, I want to give my answer of this problem. I think this answer is the most ingenious one. This is a proof without words as following.
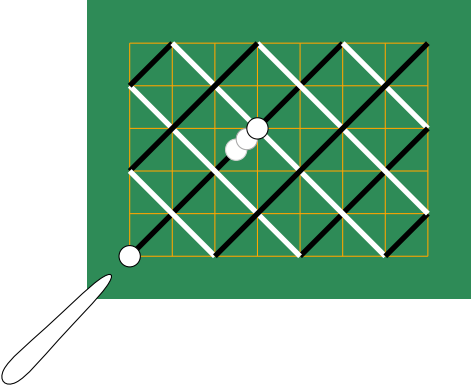
When I heared the problem, I had no papers and pen to use. After thinking over brokenly, I came up the answer above one day after. And one can easy to find that in the case of one of $m,n$ is even, then the difference between black and white vanish, and when $m,n$ are odd generally, the difference is $(m,n)$.
Ackowlegement
I want to thank Liu Ben for his nice presentation of question and answer. And congratulation to his addmision by ENS.
