数据结构理论基础-6—图

Table of Contents

1.图

1.1各种图定义

C语言具体实现见：数据结构C语言实现-6—图

1.图

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为G（V，E），其中，G 表示一个图，V 是图 G 中顶点的集合，E 是图 G 中边的集合。

线性表中将数据元素称为元素，树中将数据元素叫结点，在图中数据元素称之为顶点（Vertex）。在图中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示。

1.1各种图定义

无向边：若顶点 $V_{i}$ 到 $V_{j}$ 之间的边没有方向，则称这条边为无向边（Edge），用无序偶对 $(V_{i}, V_{j})$ 来表示。

无向图：图中任意两个顶点之间的边都是无向边。

对于下图的无向图 $G_{1}$ ， $G_{1}=(V_{1}, \left \{ E_{1} \right \})$ ，其中顶点集合 $V_{1}=\left \{ A, B, C, D \right \}$ ，边集合 $E_{1}=\left \{ (A,B), (B,C), (C,D), (D,A), (A,C) \right \}$

有向边：若从顶点 $V_{i}$ 到 $V_{j}$ 的边有方向，则称这条边为有向边，也成为弧，用有序偶 $<V_{i}, V_{j}>$ ， $V_{i}$ 称为弧尾， $V_{j}$ 称为弧头.

有向图：图中任意两个顶点之间的边都是有向边

对于下图的有向图 $G_{2}$ ， $G_{2}=(V_{2}, \left \{ E_{2} \right \})$ ，其中顶点集合 $V_{2}=\left \{ A, B, C, D \right \}$ ，连接顶点 A 到 D 的有向边就是弧，A 是弧尾，D 是弧头， $<A, D>$ 表示弧，注意不能写成 $<D, A>$ 。弧集合 $E_{2}=\left \{ <A,D>, <B,A>, <C,A>, <B,C> \right \}$

无向完全图：在无向图中，如果任意两个顶点之间都存在边。含有 n 个顶点的无向完全图有n(n-1) / 2条边。

有向完全图：在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧。含有 n 个顶点的有向完全图有 n(n-1)条边。

有些图的边或弧具有与它相关的数字，这种与图的边或弧相关的数叫做权（Weight），这种带权的图通常称为网（Network）.

假设有两个图 $G=(V,\left \{ E \right \}})$ 和 $G^{'}=(V^{'}, \left \{ E' \right \})$ ，如果 $V^{'}\subseteq V$ 且 $E^{'}\subseteq E$ ，则称 $G^{'}$ 为G的子图（Subgraph）

对于无向图 $G=(V,\left \{ E \right \}})$ ，顶点 V 的度（Degree）是和 V 相关联的边的数目，记为TD( V )。对于无向图来说，边数就是各顶点度数和的一半.

对于有向图 $G=(V,\left \{ E \right \}})$ ，以顶点 V 为头的弧的数目称为 V 的入度（InDegree）记为ID(V)；以 V 为尾的弧的数目称为 V 的出度（OutDegree）记为OD(V)；顶点 V 的度为TD(v) = ID(v) + OD(v)。

在无向图 G 中，如果从顶点 V 到顶点 V' 有路径，则称 V 和 V'是连通的，如果对于图中任意两个顶点 $V_{i}, V_{j}\in E$ ， $V_{i}$ 和 $V_{j}$ 都是连通的，则称 G 是连通图（Connected Graph）

在有向图 G 中，如果从顶点 V 到顶点 V' 有路径，则称 V 和 V'是连通的，如果对于每一对 $V_{i}, V_{j}\in E$ ， $V_{i}\neq V_{j}$ ，从 $V_{i}$ 到 $V_{j}$ 和从 $V_{j}$ 到 $V_{i}$ 都存在路径，则称 G 是强连通图

2.图的存储结构

图的抽象数据类型

ADT 图（Graph）

Data

顶点的有穷非空集合和边的集合。

Operation

CreateGraph(*G, V, VR)：按照顶点集 V 和边弧集 VR 的定义构造图G；

DestroyGraph(*G)：图 G 存在则销毁；

LocateVex(G, u)：若图 G 中存在顶点 u，则返回图中的位置；

GetVex(G, v)：返回图 G 中顶点 v 的值；

PutVex(G, v, value)：将图 G 中的顶点 v 赋值 value；

FirstAdjVex(G, *v)：返回顶点 v 的一个邻接顶点，若顶点在 G 中无邻接顶点返回空；

NextAdjVex(G, v, *w)：返回顶点 v 相对于顶点 w 的下一个邻接顶点；若 w 是 v 的最后一个邻接顶点则返回空；

InsertVex(*G, v)：在图 G 中增添新顶点 v；

DeleteVex(*G, v)：删除图 G 中顶点 v 及其相关的弧；

InsertArc(*G, v, w)：在图 G 中增添弧<v, w>;

DeleteArc(*G, v, w)：在图 G 中删除弧<v, w>;

DFSTraverse(G)：对图 G 进行深度优先遍历，在遍历过程对每个顶点调用；

HFSTraverse(G)：对图 G 进行广度优先遍历，在遍历过程对每个顶点调用；

由于图的结构比较复杂，任意两个顶点之间都可能存在联系，因此无法以数据元素在内存中的物理位置来表示元素之间的关系，也就是说图不可能用简单的顺序存储结构来表示。接下来介绍五种不同的存储结构。

2.1邻接矩阵

图的邻接矩阵（Adjacency Matrix）存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。

设图 G 有 n 个顶点，则邻接矩阵是一个 n x n 的方阵，定义为：

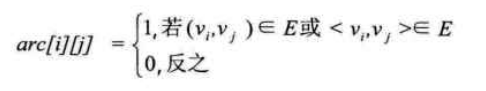
设图 G 是网图，有 n 个顶点，则邻接矩阵是一个 n x n 的方阵，定义为：

邻接矩阵存储结构代码：

typedef char VertexType; /* 顶点类型应由用户定义  */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */
#define MAXVEX 100 /* 最大顶点数，应由用户定义 */
#define InFINITY 65535 /* 用65535来代表无穷大 */
typedef struct
{
	VertexType vexs[MAXVEX]; /* 顶点表 */
	EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵，可看作边表 */
	int numNodes, numEdges; /* 图中当前的顶点数和边数  */
}MGraph;

/* 建立无向网图的邻接矩阵表示 */
void CreateMGraph(MGraph *G)
{
	int i,j,k,w;
	printf("输入顶点数和边数:\n");
	scanf("%d,%d",&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */
	for(i = 0;i < G->numNodes;i++) /* 读入顶点信息,建立顶点表 */
		scanf(&G->vexs[i]);
	for(i = 0;i < G->numNodes;i++)
		for(j = 0;j < G->numNodes;j++)
			G->arc[i][j]=INFINITY;	/* 邻接矩阵初始化 */
	for(k = 0;k < G->numEdges;k++) /* 读入numEdges条边，建立邻接矩阵 */
	{
		printf("输入边(vi,vj)上的下标i，下标j和权w:\n");
		scanf("%d,%d,%d",&i,&j,&w); /* 输入边(vi,vj)上的权w */
		G->arc[i][j]=w; 
		G->arc[j][i]= G->arc[i][j]; /* 因为是无向图，矩阵对称 */
	}
}

2.2邻接表

邻接表是一种数组与链表相结合的存储方法。图中顶点用一维数组存储，在顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，图中每个顶点 v 的所有邻接点构成一个线性表，用单链表存储。

从上图中可知，顶点表的各个结点由 data 和 firstedge 两个域表示，data 是数据域存储顶点的信息，firstedge是指针域，指向边表的第一个结点；边表结点由 adjvex 和 next 两个域组成，adjvex 是邻接点域，存储某顶点的邻接点在顶点表中的下标，next 存储指向边表中下一个结点的指针。

有向图的邻接表是以顶点为弧尾来存储边表的，这样能够很容易得到每个顶点的出度，但不容易得出顶点的入度，所以可以建立一个有向图的逆邻接表。

typedef char VertexType; /* 顶点类型应由用户定义 */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */

typedef struct EdgeNode /* 边表结点  */
{
	int adjvex;    /* 邻接点域,存储该顶点对应的下标 */
	EdgeType info;		/* 用于存储权值,对于非网图可以不需要 */
	struct EdgeNode *next; /* 链域,指向下一个邻接点 */
}EdgeNode;

typedef struct VertexNode /* 顶点表结点 */
{
	VertexType data; /* 顶点域,存储顶点信息 */
	EdgeNode *firstedge;/* 边表头指针 */
}VertexNode, AdjList[MAXVEX];

typedef struct
{
	AdjList adjList; 
	int numNodes,numEdges; /* 图中当前顶点数和边数 */
}GraphAdjList;

/* 建立图的邻接表结构 */
void  CreateALGraph(GraphAdjList *G)
{
	int i,j,k;
	EdgeNode *e;
	printf("输入顶点数和边数:\n");
	scanf("%d,%d",&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */
	for(i = 0;i < G->numNodes;i++) /* 读入顶点信息,建立顶点表 */
	{
		scanf(&G->adjList[i].data); 	/* 输入顶点信息 */
		G->adjList[i].firstedge=NULL; 	/* 将边表置为空表 */
	}
	
	
	for(k = 0;k < G->numEdges;k++)/* 建立边表 */
	{
		printf("输入边(vi,vj)上的顶点序号:\n");
		scanf("%d,%d",&i,&j); /* 输入边(vi,vj)上的顶点序号 */
		e=(EdgeNode *)malloc(sizeof(EdgeNode)); /* 向内存申请空间,生成边表结点 */
		e->adjvex=j;					/* 邻接序号为j */                         
		e->next=G->adjList[i].firstedge;	/* 将e的指针指向当前顶点上指向的结点 */
		G->adjList[i].firstedge=e;		/* 将当前顶点的指针指向e */               
		
		e=(EdgeNode *)malloc(sizeof(EdgeNode)); /* 向内存申请空间,生成边表结点 */
		e->adjvex=i;					/* 邻接序号为i */                         
		e->next=G->adjList[j].firstedge;	/* 将e的指针指向当前顶点上指向的结点 */
		G->adjList[j].firstedge=e;		/* 将当前顶点的指针指向e */               
	}
}

2.3十字链表

我们可以看到，有向图的邻接表是有缺陷的，对于入度或出度，我们只能单方面得出一个，对此十字链表就是把邻接表和逆邻接表结合在一起。重新定义顶点表结点结构如下：

firstin 表示入边表头指针，指向该顶点的入边表中第一个结点，firstout 表示出边表头指针，指向该顶点的出边表中的第一个结点。

重新定义边表结点结构如下：

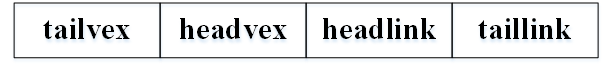
tailvex 是指弧起点在顶点表的下标，headvex 是指弧终点在顶点表中的下标，headlink 是指入边表指针域，指向终点相同的下一条边，taillink 是指边表指针域，指向起点相同的下一条边。

2.4邻接多重表

十字链表是对有向图的邻接表做出的改进，而邻接多重表是对无向图的邻接表做出的改进。无向图的邻接表对于点的操作是方便的，但是如果关注的重点是对边的操作（例如删除一条边），无向图的邻接表是比较繁琐的。重新定义边表结点结构如下：

ivex 和 jvex 是与某条边依附的两个顶点在顶点表中的下标。ilink 指向依附顶点 ivex 的下一条边，jlink 指向依附顶点 jvex 的下一条边。

2.5边集数组

边集数组是由两个一维数组构成，一个是存储顶点的信息，另一个是存储边的信息。

边数组结构：

begin 存储起点下标，end 存储终点下标，weight 存储权值。

3图的遍历

图的遍历（Traversing Graph）：从图中某一个顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次。

3.1深度优先遍历

深度优先遍历（Depth First Search），简称为DFS。

如下图中的左图所示，从顶点 A 开始走遍所有的图顶点并作上标记，在没有碰到重复顶点下，始终向右手边走。如果按照深度优先遍历的话，就会如右图所示。按照这种顺序走完：A -> B -> C -> D -> E -> F -> G -> H -> I

可以看出，深度优先遍历其实就是一个递归的过程，而且就像一棵树的前序遍历。它从图中某个顶点 v 出发，访问此顶点，然后从 v 的未被访问的邻接点出发深度优先遍历图，直至图中所有和 v 有路径相通的顶点都被访问到。

邻接矩阵的深度优先遍历算法代码如下：

typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */
Boolean visited[MAXVEX]; /* 访问标志的数组 */

/* 邻接矩阵的深度优先递归算法 */
void DFS(MGraph G, int i)
{
	int j;
 	visited[i] = TRUE;
 	printf("%c ", G.vexs[i]);/* 打印顶点，也可以其它操作 */
	for(j = 0; j < G.numVertexes; j++)
		if(G.arc[i][j] == 1 && !visited[j])
 			DFS(G, j);/* 对为访问的邻接顶点递归调用 */
}

/* 邻接矩阵的深度遍历操作 */
void DFSTraverse(MGraph G)
{
	int i;
 	for(i = 0; i < G.numVertexes; i++)
 		visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */
	for(i = 0; i < G.numVertexes; i++)
 		if(!visited[i]) /* 对未访问过的顶点调用DFS，若是连通图，只会执行一次 */ 
			DFS(G, i);
}

邻接表的深度优先遍历算法代码如下：

/* 邻接表的深度优先递归算法 */
void DFS(GraphAdjList GL, int i)
{
	EdgeNode *p;
 	visited[i] = TRUE;
 	printf("%c ",GL->adjList[i].data);/* 打印顶点,也可以其它操作 */
	p = GL->adjList[i].firstedge;
	while(p)
	{
 		if(!visited[p->adjvex])
 			DFS(GL, p->adjvex);/* 对为访问的邻接顶点递归调用 */
		p = p->next;
 	}
}

/* 邻接表的深度遍历操作 */
void DFSTraverse(GraphAdjList GL)
{
	int i;
 	for(i = 0; i < GL->numVertexes; i++)
 		visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */
	for(i = 0; i < GL->numVertexes; i++)
 		if(!visited[i]) /* 对未访问过的顶点调用DFS,若是连通图,只会执行一次 */ 
			DFS(GL, i);
}

3.2广度优先遍历

广度优先遍历（Breadth First Search），简称为BFS。

如果说图的深度优先遍历类似于树的前序遍历，那么图的广度优先遍历就类似于树的层序遍历。

将下图中的左图稍微变形一下，变换成右图，但是顶点和边的关系没有变。

邻接矩阵的广度优先遍历算法代码如下：

/* 邻接矩阵的广度遍历算法 */
void BFSTraverse(MGraph G)
{
	int i, j;
	Queue Q;
	for(i = 0; i < G.numVertexes; i++)
       	visited[i] = FALSE;
    InitQueue(&Q);		/* 初始化一辅助用的队列 */
    for(i = 0; i < G.numVertexes; i++)  /* 对每一个顶点做循环 */
    {
		if (!visited[i])	/* 若是未访问过就处理 */
		{
			visited[i]=TRUE;		/* 设置当前顶点访问过 */
			printf("%c ", G.vexs[i]);/* 打印顶点，也可以其它操作 */
			EnQueue(&Q,i);		/* 将此顶点入队列 */
			while(!QueueEmpty(Q))	/* 若当前队列不为空 */
			{
				DeQueue(&Q,&i);	/* 将队对元素出队列，赋值给i */
				for(j=0;j<G.numVertexes;j++) 
				{ 
					/* 判断其它顶点若与当前顶点存在边且未访问过  */
					if(G.arc[i][j] == 1 && !visited[j]) 
					{ 
 						visited[j]=TRUE;			/* 将找到的此顶点标记为已访问 */
						printf("%c ", G.vexs[j]);	/* 打印顶点 */
						EnQueue(&Q,j);				/* 将找到的此顶点入队列  */
					} 
				} 
			}
		}
	}
}

邻接表的广度优先遍历算法代码如下：

/* 邻接表的广度遍历算法 */
void BFSTraverse(GraphAdjList GL)
{
	int i;
    EdgeNode *p;
	Queue Q;
	for(i = 0; i < GL->numVertexes; i++)
       	visited[i] = FALSE;
    InitQueue(&Q);
   	for(i = 0; i < GL->numVertexes; i++)
   	{
		if (!visited[i])
		{
			visited[i]=TRUE;
			printf("%c ",GL->adjList[i].data);/* 打印顶点,也可以其它操作 */
			EnQueue(&Q,i);
			while(!QueueEmpty(Q))
			{
				DeQueue(&Q,&i);
				p = GL->adjList[i].firstedge;	/* 找到当前顶点的边表链表头指针 */
				while(p)
				{
					if(!visited[p->adjvex])	/* 若此顶点未被访问 */
 					{
 						visited[p->adjvex]=TRUE;
						printf("%c ",GL->adjList[p->adjvex].data);
						EnQueue(&Q,p->adjvex);	/* 将此顶点入队列 */
					}
					p = p->next;	/* 指针指向下一个邻接点 */
				}
			}
		}
	}
}

4.最小生成树

如下图所示，这是一个网结构图，找出连接所有顶点的最短路径。

下图就是两种方案，我们把构造连通网的最小代价生成树称为最小生成树。找最小生成树，经典的有两种算法，普里姆算法（P算法）和克鲁斯卡尔算法（K算法）。

4.1普里姆（Prim）算法

P算法的特点是：以某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树，即：顺序取结点，边取最小值。

如下图所示：

找出与顶点 $V_{0}$ 相连的最小路径，发现 $V_{0}$ 到 $V_{1}$ 路径最短，记为（0，1）
找出与顶点 $V_{0}$ 、 $V_{1}$ 相连的最小路径，发现 $V_{0}$ 到 $V_{5}$ 路径最短，记为（0，5）
找出与顶点 $V_{0}$ 、 $V_{1}$ 、 $V_{5}$ 相连的最小路径，发现 $V_{1}$ 到 $V_{8}$ 路径最短，记为（1，8）
找出与顶点 $V_{0}$ 、 $V_{1}$ 、 $V_{5}$ 、 $V_{8}$ 相连的最小路径，发现 $V_{8}$ 到 $V_{2}$ 路径最短，记为（8，2）
......
最终经过 P 算法之后，最小生成树为（0，1）、（0，5）、（1，8）、（8，2）、（1，6）、（6，7）、（7，4）、（7，3）

Prim算法代码如下：

/* Prim算法生成最小生成树  */
void MiniSpanTree_Prim(MGraph G)
{
	int min, i, j, k;
	int adjvex[MAXVEX];		/* 保存相关顶点下标 */
	int lowcost[MAXVEX];	/* 保存相关顶点间边的权值 */
	lowcost[0] = 0;/* 初始化第一个权值为0，即v0加入生成树 */
			/* lowcost的值为0，在这里就是此下标的顶点已经加入生成树 */
	adjvex[0] = 0;			/* 初始化第一个顶点下标为0 */
	for(i = 1; i < G.numVertexes; i++)	/* 循环除下标为0外的全部顶点 */
	{
		lowcost[i] = G.arc[0][i];	/* 将v0顶点与之有边的权值存入数组 */
		adjvex[i] = 0;					/* 初始化都为v0的下标 */
	}
	for(i = 1; i < G.numVertexes; i++)
	{
		min = INFINITY;	/* 初始化最小权值为∞， */
						/* 通常设置为不可能的大数字如32767、65535等 */
		j = 1;k = 0;
		while(j < G.numVertexes)	/* 循环全部顶点 */
		{
			if(lowcost[j]!=0 && lowcost[j] < min)/* 如果权值不为0且权值小于min */
			{	
				min = lowcost[j];	/* 则让当前权值成为最小值 */
				k = j;			/* 将当前最小值的下标存入k */
			}
			j++;
		}
		printf("(%d, %d)\n", adjvex[k], k);/* 打印当前顶点边中权值最小的边 */
		lowcost[k] = 0;/* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */
		for(j = 1; j < G.numVertexes; j++)	/* 循环所有顶点 */
		{
			if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) 
			{/* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */
				lowcost[j] = G.arc[k][j];/* 将较小的权值存入lowcost相应位置 */
				adjvex[j] = k;				/* 将下标为k的顶点存入adjvex */
			}
		}
	}
}

4.2克鲁斯卡尔（Kruskal）算法

k算法是直接以边为目标去构建的，也就是顺序取边

k算法的做法是依次取出最小的边，且不能形成环路，此处不详细讲解，最终的结构是(4, 7) 7、(2, 8) 8、(0, 1) 10、(0, 5) 11、(1, 8) 12、(3, 7) 16、(1, 6) 16、(6, 7) 19

/* 对边集数组Edge结构的定义 */
typedef struct
{
	int begin;
	int end;
	int weight;
}Edge;  

/* 生成最小生成树 */
void MiniSpanTree_Kruskal(MGraph G)
{
	int i, j, n, m;
	int k = 0;
	int parent[MAXVEX];/* 定义一数组用来判断边与边是否形成环路 */
	
	Edge edges[MAXEDGE];/* 定义边集数组,edge的结构为begin,end,weight,均为整型 */

	/* 用来构建边集数组并排序********************* */
	for ( i = 0; i < G.numVertexes-1; i++)
	{
		for (j = i + 1; j < G.numVertexes; j++)
		{
			if (G.arc[i][j]<INFINITY)
			{
				edges[k].begin = i;
				edges[k].end = j;
				edges[k].weight = G.arc[i][j];
				k++;
			}
		}
	}
	sort(edges, &G);
	/* ******************************************* */


	for (i = 0; i < G.numVertexes; i++)
		parent[i] = 0;	/* 初始化数组值为0 */

	printf("打印最小生成树：\n");
	for (i = 0; i < G.numEdges; i++)	/* 循环每一条边 */
	{
		n = Find(parent,edges[i].begin);
		m = Find(parent,edges[i].end);
		if (n != m) /* 假如n与m不等，说明此边没有与现有的生成树形成环路 */
		{
			parent[n] = m;	/* 将此边的结尾顶点放入下标为起点的parent中。 */
							/* 表示此顶点已经在生成树集合中 */
			printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
		}
	}
}

克鲁斯卡尔（K算法）算法主要是针对边来展开的，边数少时效率会非常高，所以对于稀疏图有很大的优势，而普里姆（P算法）算法对于稠密图，即边数非常多的情况会更好一些。

5最短路径

对于网图来说，最短路径是指两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点

5.1迪杰斯特拉（Dijkstra）算法

迪杰斯特拉（D算法）算法是逐步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到你要的结果。

如下图：求出其余点到 $V_{s}$ 的最短路径， $W_{j}$ 为最短路径长（暂定值）

#define MAXVEX 20
#define INFINITY 65535
typedef int Patharc[MAXVEX];    /* 用于存储最短路径下标的数组 */
typedef int ShortPathTable[MAXVEX];/* 用于存储到各点最短路径的权值和 */

/*  Dijkstra算法，求有向网G的v0顶点到其余顶点v的最短路径P[v]及带权长度D[v] */    
/*  P[v]的值为前驱顶点下标,D[v]表示v0到v的最短路径长度和 */  
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable *D)
{    
	int v,w,k,min;    
	int final[MAXVEX];/* final[w]=1表示求得顶点v0至vw的最短路径 */
	for(v=0; v<G.numVertexes; v++)    /* 初始化数据 */
	{        
		final[v] = 0;			/* 全部顶点初始化为未知最短路径状态 */
		(*D)[v] = G.arc[v0][v];/* 将与v0点有连线的顶点加上权值 */
		(*P)[v] = -1;				/* 初始化路径数组P为-1  */       
	}

	(*D)[v0] = 0;  /* v0至v0路径为0 */  
	final[v0] = 1;    /* v0至v0不需要求路径 */        
	/* 开始主循环，每次求得v0到某个v顶点的最短路径 */   
	for(v=1; v<G.numVertexes; v++)   
	{
		min=INFINITY;    /* 当前所知离v0顶点的最近距离 */        
		for(w=0; w<G.numVertexes; w++) /* 寻找离v0最近的顶点 */    
		{            
			if(!final[w] && (*D)[w]<min)             
			{                   
				k=w;                    
				min = (*D)[w];    /* w顶点离v0顶点更近 */            
			}        
		}        
		final[k] = 1;    /* 将目前找到的最近的顶点置为1 */
		for(w=0; w<G.numVertexes; w++) /* 修正当前最短路径及距离 */
		{
			/* 如果经过v顶点的路径比现在这条路径的长度短的话 */
			if(!final[w] && (min+G.arc[k][w]<(*D)[w]))   
			{ /*  说明找到了更短的路径，修改D[w]和P[w] */
				(*D)[w] = min + G.arc[k][w];  /* 修改当前路径长度 */               
				(*P)[w]=k;        
			}       
		}   
	}
}

5.2弗洛伊德（Floyd）算法

弗洛伊德（F算法）算法是求所有端间最短径算法。用矩阵进行系统化的计算，径长矩阵 $W_{n\times n}$ 和转接矩阵 $R_{n\times n}$ 表示为：

typedef int Patharc[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];

/* Floyd算法，求网图G中各顶点v到其余顶点w的最短路径P[v][w]及带权长度D[v][w]。 */    
void ShortestPath_Floyd(MGraph G, Patharc *P, ShortPathTable *D)
{    
	int v,w,k;    
	for(v=0; v<G.numVertexes; ++v) /* 初始化D与P */  
	{        
		for(w=0; w<G.numVertexes; ++w)  
		{
			(*D)[v][w]=G.arc[v][w];	/* D[v][w]值即为对应点间的权值 */
			(*P)[v][w]=w;				/* 初始化P */
		}
	}
	for(k=0; k<G.numVertexes; ++k)   
	{
		for(v=0; v<G.numVertexes; ++v)  
		{        
			for(w=0; w<G.numVertexes; ++w)    
			{
				if ((*D)[v][w]>(*D)[v][k]+(*D)[k][w])
				{/* 如果经过下标为k顶点路径比原两点间路径更短 */
					(*D)[v][w]=(*D)[v][k]+(*D)[k][w];/* 将当前两点间权值设为更小的一个 */
					(*P)[v][w]=(*P)[v][k];/* 路径设置为经过下标为k的顶点 */
				}
			}
		}
	}
}

6.拓扑排序

在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图网，称为 AVO 网（Activity On Vertex Network).

设 G =（V, E）是一个具有 n 个顶点的有向图，V 中的顶点序列 $v_{1}, v_{2},...,v_{n}$ ，满足若从顶点 $v_{i}$ 到 $v_{j}$ 有一条路径，则在顶点序列中顶点 $v_{i}$ 必在顶点 $v_{j}$ 之前。则我们称这样的顶点序列为一个拓扑结构。拓扑排序其实就是对一个有向图构造拓扑序列的过程 。

对 AOV 网进行拓扑排序的基本思路是：从 AOV 网中选择一个入度为 0 的顶点输出，然后删去此顶点，并删除以此顶点为尾的弧，继续重复此步骤，直到输出全部顶点或者 AOV 网中不存在入读为 0 的顶点为止。

对于如下的 AOV 网，可得到邻接表数据结构如下：

结构代码如下：

/* 邻接矩阵结构 */
typedef struct
{
	int vexs[MAXVEX];
	int arc[MAXVEX][MAXVEX];
	int numVertexes, numEdges;
}MGraph;

/* 邻接表结构****************** */
typedef struct EdgeNode /* 边表结点  */
{
	int adjvex;    /* 邻接点域，存储该顶点对应的下标 */
	int weight;		/* 用于存储权值，对于非网图可以不需要 */
	struct EdgeNode *next; /* 链域，指向下一个邻接点 */
}EdgeNode;

typedef struct VertexNode /* 顶点表结点 */
{
	int in;	/* 顶点入度 */
	int data; /* 顶点域，存储顶点信息 */
	EdgeNode *firstedge;/* 边表头指针 */
}VertexNode, AdjList[MAXVEX];

typedef struct
{
	AdjList adjList; 
	int numVertexes,numEdges; /* 图中当前顶点数和边数 */
}graphAdjList,*GraphAdjList;

/* 拓扑排序，若GL无回路，则输出拓扑排序序列并返回1，若有回路返回0。 */
Status TopologicalSort(GraphAdjList GL)
{    
	EdgeNode *e;    
	int i,k,gettop;   
	int top=0;  /* 用于栈指针下标  */
	int count=0;/* 用于统计输出顶点的个数  */    
	int *stack;	/* 建栈将入度为0的顶点入栈  */   
	stack=(int *)malloc(GL->numVertexes * sizeof(int) );    

	for(i = 0; i<GL->numVertexes; i++)                
		if(0 == GL->adjList[i].in) /* 将入度为0的顶点入栈 */         
			stack[++top]=i;    
	while(top!=0)    
	{        
		gettop=stack[top--];        
		printf("%d -> ",GL->adjList[gettop].data);        
		count++;        /* 输出i号顶点，并计数 */        
		for(e = GL->adjList[gettop].firstedge; e; e = e->next)        
		{            
			k=e->adjvex;            
			if( !(--GL->adjList[k].in) )  /* 将i号顶点的邻接点的入度减1，如果减1后为0，则入栈 */                
				stack[++top]=k;        
		}
	}   
	printf("\n");   
	if(count < GL->numVertexes)        
		return ERROR;    
	else       
		return OK;
}