深度学习基础算法-神经网络

2层神经网络的实现

使用Numpy矩阵来实现神经网络。我们先使用最简单的网络去实现，这个神经网络去掉了偏置和激活函数，只有权重。

这里我们假设每条线上对应的权重就是各自的数字，那么如果用函数来表示的话，应该是

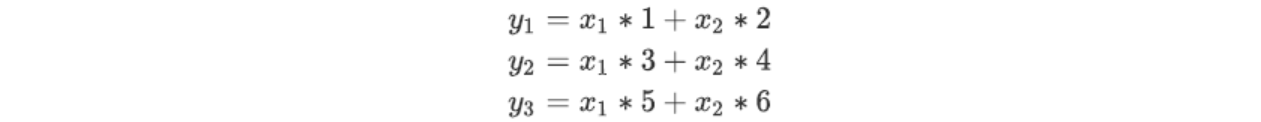
可以看到，这样的表示方法非常的复杂，不方便，因此我们把神经网络的表示方法，改变成矩阵的乘法形式：
实现该神经网络时，要注意X ，W ，Y 的形状，特别是X和W的对应维度的元素个数是否一致。假设我们的输入数据为(2，4)，那么神经网络的输出为:

# 矩阵形式
X = np.array([2,4])
W = np.array([[1,3,5],[2,4,6]])
Y = np.dot(X,W)
Y

array([10, 22, 34])

返回的结果为array([10，22，34]) ，也就是Y 的输出结果为y1=10，y2=22，y3=34，这样一来，我们就通过一次运算，算出了三个输出节点的输出值。而这种计算方法，即使我们在输出层有几百个几千个元素，也都可以通过一次运算就计算出结果，大大简化了运算的复杂程度。

3层神经网络的实现

现在我们来进行的是一个三层的复杂神经网络的实现。这里我们以下图的神经网络为对象，实现从输入到输出的处理。如图所示：
3层神经网络：输入层（第0层）有2个神经元，第1个隐藏层（第1层）有3个神经元，第2个隐藏层（第2层）有2个神经元，输出层（第3层）有2个神经元。为了进行复杂的线性代数运算，我们需要先规定符号，这些符号看起来会比较复杂：
我们首先来进行符号的定义：
α₁⁽¹⁾表示的是第1层的第1个神经元。具体来说，这个符号中的(1)表示的是神经元所在的层号，而下标1表示的是本层的第几个神经元。
ω₁₂⁽¹⁾的右下角的两个数字12，分别代表的是这个权重所表示的后一层第1个神经元和前一层第2个神经元（也就是说，权重右下角按照“后一层的索引号、前一层的索引号”的顺序排列）。右上角(1) 也是表示这个权重所处的层号。具体说明如下图：

各层之间信号的传递

有了上面规定的这种表示方式，就可以方便的用公式来表示各层之间的计算公式了。首先，来看第一层，也就是从输入层到第一层的第1个神经元的信号传递过程是怎样的。如下图：

在每一层的计算过程中，都在已有的神经元的基础上添加一个偏置神经元"1"，对于偏置神经元，因为本身没有神经元的序号，所以我们省略一个序号的标识。在α₁⁽¹⁾这个神经元中，它的信号计算公式如下:
那么，依然是如果使用矩阵乘法去进行运算，整个第一层神经元的加权和计算结果可以通过这个公式进行计算：
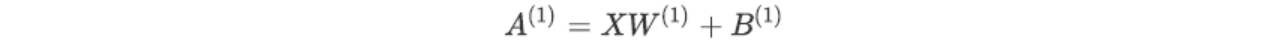其中每一部分是如下的内容：
输入层到第1层的信号传递：

#输入层到第1层的信号传递
X = np.array([1.0,0.5])
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])
print(W1.shape)     # (2，3)
print(X.shape)      # (2,)
print(B1.shape)     # (3,)
A1 = np.dot(X,W1) + B1
A1

(2, 3)
(2,)
(3,)

array([0.3, 0.7, 1.1])

W1是2*3的数组，X是元素个数为2的一维数组。这里，W1和X的对应维度的元素个数也保持了一致。接下来，我们测试第1层中激活函数的计算过程。
如下图所示，隐藏层的加权和（加权信号和偏置的总和）用α表示，被激活函数转换后的信号用z表示。此外，图中h()表示激活函数，这里我们使用的是sigmoid函数。用Python来实现，代码如下：

#被激活函数sigmoid转换后的信号
Z1 = sigmoid(A1)
print(A1) 
print(Z1)

[0.3 0.7 1.1]
[0.57444252 0.66818777 0.75026011]

下面，来实现第1层到第2层的信号传递：

#第1层到第2层的信号传递
W2 = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
B2 = np.array([0.1,0.2])
print(Z1.shape) # (3,)
print(W2.shape) # (3，2)
print(B2.shape) # (2,)
A2 = np.dot(Z1,W2) + B2
Z2 = sigmoid(A2)
print(A2)       # [0.51615984, 1.21402696]
print(Z2)       # [0.62624937, 0.7710107 ]

(3,)
(3, 2)
(2,)
[0.51615984 1.21402696]
[0.62624937 0.7710107 ]

除了第1层的输出（ Z1 ）变成了第2层的输入这一点以外，这个实现和刚才的代码完全相同。由此可知，通过使用NumPy数组，可以将层到层的信号传递过程简单地写出来。

最后是第2层到输出层的信号传递。输出层的实现也和之前的实现基本相同。不过，最后的激活函数和之前的隐藏层有所不同。输出层只需要将输出的信号原样输出就可以，实际上不需要激活函数，这里我们为了保持每一层中流程的统一，因此定义了输出层的激活函数——identity_function() 函数（称为"恒等函数"）。
输出层的激活函数用σ()表示（σ读作sigma），不同于隐藏层的激活函数h()。

#第2层到输出层的信号传递
# 定义恒等函数
def identity_function(x):
    return x

W3 = np.array([[0.1,0.3],[0.2,0.4]])
B3 = np.array([0.1,0.2])
A3 = np.dot(Z2,W3) + B3
Y = identity_function(A3) # 相当于 Y = A3
print(Y)                  # [0.31682708, 0.69627909]   

[0.31682708 0.69627909]

这里要注意的是，输出层的激活函数不是必须使用恒等函数，要根据解决的问题决定。一般来说，回归问题可以使用恒等函数。如果解决的问题是二元分类问题，就可以使用sigmoid函数，多元分类问题可以使用softmax函数。

代码整理

把之前零散的代码整理一下，了解一下整个神经网络实现的流程。
初始化神经网络的参数数据：

#初始化神经网络的参数数据
def init_network():
    network = {
        "W1":np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]]),
        'b1':np.array([0.1,0.2,0.3]),
        'W2':np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]]),
        'b2':np.array([0.1,0.2]),
        'W3':np.array([[0.1,0.3],[0.2,0.4]]),
        'b3':np.array([0.1,0.2])
        }
    return network

#测试函数
init_network()['b1']

array([0.1, 0.2, 0.3])

信号向前传播的过程函数：

#信号向前传播的过程函数
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)  
    return y

调用函数运行:

# 测试函数运行结果
network = init_network()
x = np.array([1.0, 0.5]) # 待训练样本
y = forward(network, x)  # 训练结果
print(y)                 # [0.31682708, 0.69627909]

[0.31682708 0.69627909]

init_network() 函数会进行权重和偏置的初始化，并将它们保存在字典变量 network 中。这个字典变量network 中保存了每一层所需的参数（权重和偏置）。 forward() 函数中则封装了将输入信号转换为输出信号的处理过程。另外，这里出现了forward（前向）一词，它表示的是从输入到输出方向的传递处理。后面在进行神经网络的训练时，我们将介绍后向（backward，从输出到输入方向）的处理。
至此，神经网络的前向处理的实现就完成了。通过巧妙地使用NumPy多维数组，我们高效地实现了神经网络。

输出层的设计

通过改变输出层的激活函数，可以把神经网络的功能分别用于分类问题和回归问题上。在上面我们已经说过,一般而言，回归问题用恒等函数，分类问题用softmax函数。

softmax 函数

softmax函数的数学公式如下:
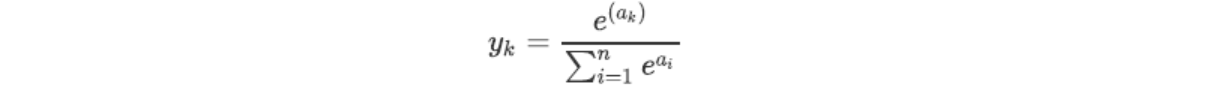公式中的n表示输出层神经元的数量，计算第k个神经元的输出y_k 。 softmax 函数的分子是输入信号α_k的指数函数，分母是所有输入信号的指数函数的和。
从公式中可以看出来，输出层的各个神经元都受到输入信号的影响。

使用Python实现softmax函数

# softmax函数
def softmax(a):
    exp_a = np.exp(a)         #指数函数
    sum_exp_a = exp_a.sum()
    y = exp_a / sum_exp_a
    return y

#测试函数运行结果
a = np.array([0.3,2.9,4.0])
softmax(a)

array([0.01821127, 0.24519181, 0.73659691])

修正softmax函数

上面的函数有一定的缺陷，因为在函数中用到了指数计算函数，所以数值增长的特别快速。而多层神经网络中，每增加一层的运算，都会导致这个数值增长很多。比如：

# softmax函数的缺陷
np.exp(100)  #2.6881171418161356e+43
np.exp(1000) #inf

inf

你会发现达到e¹⁰⁰⁰结果就没有办法正确计算了，会返回inf，导致结果产生错误。因此我们对softmax函数的公式进行进一步的推导:
首先，在分子和分母上都乘上C这个任意的常数（因为同时对分母和分子乘以相同的常数，所以计算结果不变）。然后，把这个C移动到指数函数（exp）中，记为log C。最后，把log C替换为另一个符号C’。
在进行softmax的指数函数的运算时，加上（或者减去）某个常数并不会改变运算的结果。这里的C可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值。来看一个具体的例子。

a = np.array([1010, 1000, 990])
np.exp(a) / np.sum(np.exp(a)) #返回 array([nan, nan, nan])，没有被正确计算

array([nan, nan, nan])

c = np.max(a) 
np.exp(a - c) / np.sum(np.exp(a - c))   #array([ 9.99954600e-01，4.53978686e-05，2.06106005e-09])

array([9.99954600e-01, 4.53978686e-05, 2.06106005e-09])

这样一来原本无法计算的数值，就可以正确的进行计算了，所说我们把softmax函数进行以下的改造:

# 修改后的softmax函数
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)     # 防止溢出
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

测试函数运行结果：

#测试函数运行结果
a = np.array([0.3,2.9,4.0])
y = softmax(a)
print(y)
np.sum(y)

[0.01821127 0.24519181 0.73659691]

1.0

softmax函数的特征

softmax函数的输出是从0到1之间的实数，而且多个输出值的总和是1。正是因为有了这个性质，我们才可以把softmax 函数的输出解释为"概率“ 。 这样我们就可以把上面的输出结果解释成第一类的概率是 0.018（1.8 %），第二类的概率是0.245（24.5 %），第三类的概率是0.737（73.7 %）。
所以如果一个分类问题，我们就可以认为这个样本的分类结果应该是第2类（三种类别分别为第0类，第1类，第2类）。也就是说，通过使用softmax函数，我们可以用概率的（统计的）方法处理问题。
但是softmax函数还有一个需要注意的问题，就是在使用了softmax函数之后，各个元素之间的大小关系并不会随着改变。因为e^x是单调递增函数，也就是说原来信号比较大的，带入softmax函数之
后，仍然是大的，原来小的信号也仍然是小的。因此，在使用了softmax函数之后，输出值最大的神经元的位置也不会变。所以在神经网络进行分类的时候，若不需要了解具体分类问题每一类的概率是多少，而只需要知道最终的分类结果，其实softmax函数是可以省略的。
在实际问题中，由于softmax会消耗一定运算量，一般来说都会被省略掉。