素数判定的一些讨论（Miller-Rabin算法）

一类问题： 判定一个整数n(n>1)是否为素数。

算法一：

直接根据素数的定义枚举ii从22到(n−1)(n−1)，如果n%i==0

n

n

n为合数。 时间复杂度： O ( n )

O(n)

int is_prime(int n)

{ int i; for(i = 2; i < n; i++) if(n % i == 0)

            return 0; return 1; }

算法二：

发现若存在 i<ni<n 使得 n%i==0 ，则必有 n%(n/i)==0 。
所以只需枚举 ii 从 22 到 sqrt(n)sqrt(n) 即可。

时间复杂度：O(√−√−√n)O(n−

O(n−−√) O

int is_prime(int n)

{ int i; for(i = 2; i * i <= n; i++) if(n % i == 0)

            return 0; return 1;

}

原文 https://blog.csdn.net/ECNU_LZJ/article/details/72675595

看完了上面的引理，那就可以正式开始Miller-Rabin算法的讲解了。

背景：

素性测试(即测试给定的数是否为素数)是近代密码学中的一个非常重要的课题。虽然Wilson定理(对于给定的正整数n，n是素数的充要条件为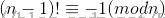)给出了一个数是素数的充要条件，但根据它来素性测试所需的计算量太大，无法实现对较大整数的测试。目前，尽管高效的确定性的素性算法尚未找到，但已有一些随机算法可用于素性测试及大整数的因数分解。下面描述的Miller-Rabin素性测试算法就是一个这样的算法。

算法：

首先要知道费马定理只是n是素数的必要条件。即费马定理不成立，n一定是合数；费马定理成立，n可能是素数。接下来请看Miller-Rabin算法的分析过程。

代码

typedef long long int ll;

ll mod_mul(ll a, ll b, ll mod)
{
    ll res = 0;
    while (b)
    {
        if (b & 1)
            res = (res + a) % mod;
        a = (a + a) % mod;
        b >>= 1;
    }
    return res;
}

ll mod_pow(ll a, ll n, ll mod)
{
    ll res = 1;
    while (n)
    {
        if (n & 1)
            res = mod_mul(res, a, mod);
        a = mod_mul(a, a, mod);
        n >>= 1;
    }
    return res;
}

// Miller-Rabin随机算法检测n是否为素数
bool Miller_Rabin(ll n)
{
    if (n == 2)
        return true;
    if (n < 2 || !(n & 1))
        return false;
    ll m = n - 1, k = 0;
    while (!(m & 1))
    {
        k++;
        m >>= 1;
    }
    for (int i = 1; i <= 20; i++)  // 20为Miller-Rabin测试的迭代次数
    {
        ll a = rand() % (n - 1) + 1;
        ll x = mod_pow(a, m, n);
        ll y;
        for (int j = 1; j <= k; j++)
        {
            y = mod_mul(x, x, n);
            if (y == 1 && x != 1 && x != n - 1)
                return false;
            x = y;
        }
        if (y != 1)
            return false;
    }
    return true;
}