用克鲁斯卡尔(Kruskal)算法构造最小生成树(最小支撑树)

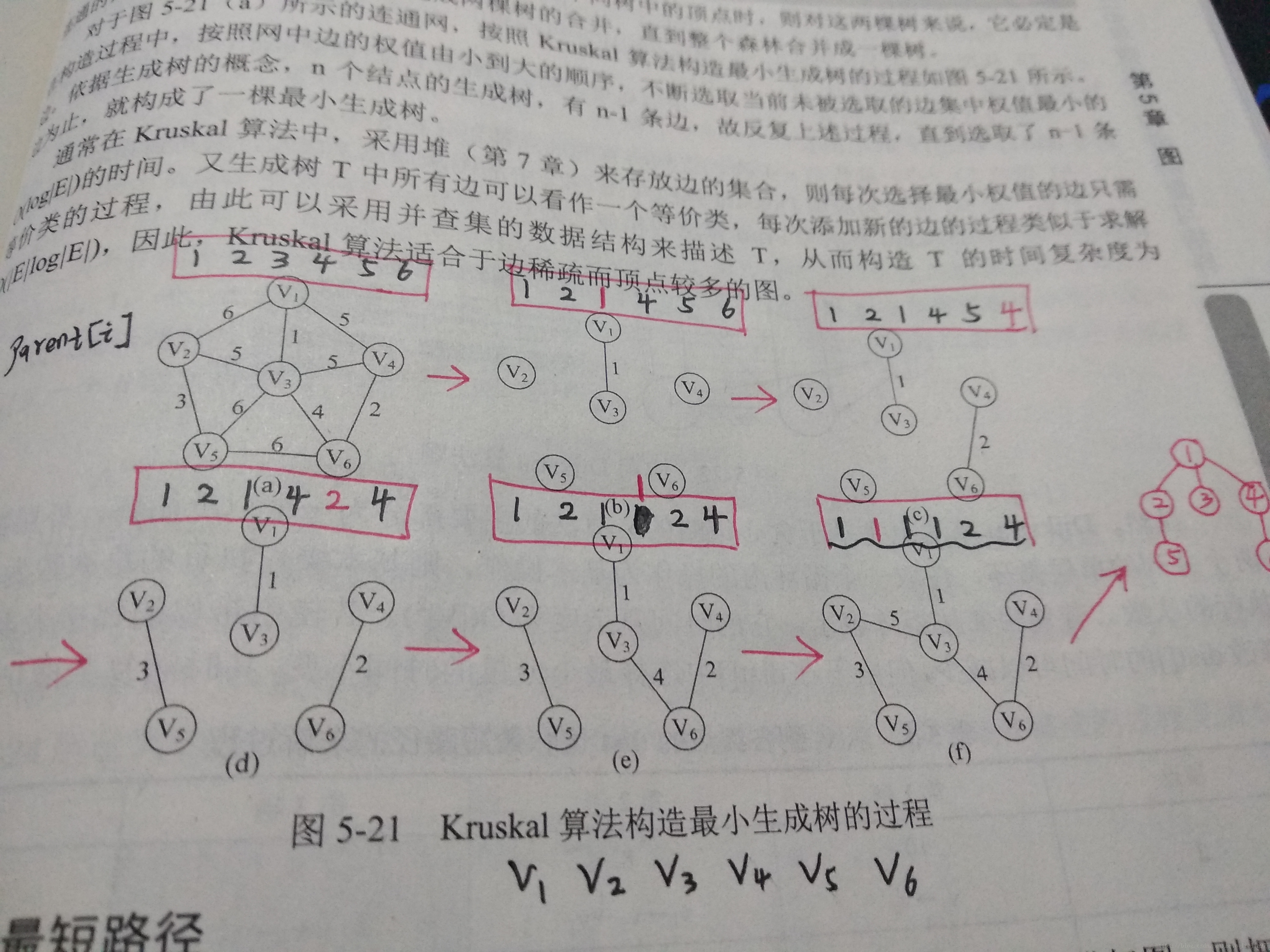
Kruskal算法和Prim算法相比，就是Kruskal算法从边出发，不断寻找当前未添加进Et的、且权值最小的边，若添加后不形成环，则添加成功；否则跳过，继续尝试添加下一条边。最后，判断边的数量arcnum是否是点的数量vexnum-1，若是则最小生成树构造成功，否则失败。

Prim算法与顶点相关时间复杂度O（|V|²），所以适合顶点少边多的图；

Kruskal反之，算法与边相关，时间复杂度为O（|E|log|E|），所以适合边少顶点多的图；

首先Vt中没有边，直接选取权值最小的边，即V1--V3，之后V3的parent更新，更新为parent[3] = 1，表明顶点V3的根节点为V1；

(c)、(d)、(e)图同理，现在到(f)，而目前权值最小的是5，有V1--V4，V3--V4，V2--V3这三条边，选择哪条呢？如果添加前面两条，则会形成环，这不符合最小生成树，所以只能添加V1--V4这条边

关键是如何判断是否形成了环呢？这就需要用到并查集的知识了。这里的条件是，若一条边的2个顶点，它们通过并查集查询到的根节点若相同，则判定形成了环。

什么是并查集呢？并查集是一种树形结构，又叫“不相交集合”，保持了一组不相交的动态集合，每个集合通过一个代表来识别，代表即集合中的某个成员，通常选择根做这个代表。

这里到(d)图时，V3的根节点是V1，V5的根节点是V2，V6的根节点是V4。从(d) --> (e)，连接了V3--V6，查询V3的根节点是V1，查询V6的根节点是V4，因此更新parent[4] = 1

后面同理

#include <iostream>
#include <algorithm> 
using namespace std;

//	Kruskal算法只与边有关，故这里只存储边的关系
//	并规定vstart为编号小的顶点，vend为编号大的顶点 
typedef struct{
	int vstart;
	int vend;
	int weight;
}Edge;
//	按照权值，从小到大排序 
bool edgeCmp(const Edge& e1, const Edge& e2)
{
	return e1.weight < e2.weight;
}

//	该图由arcnum条边组成 
typedef struct{ 
	int vexnum;
	int arcnum;
	vector<Edge> edge;
}Graph;

bool newGraph(Graph &g)
{
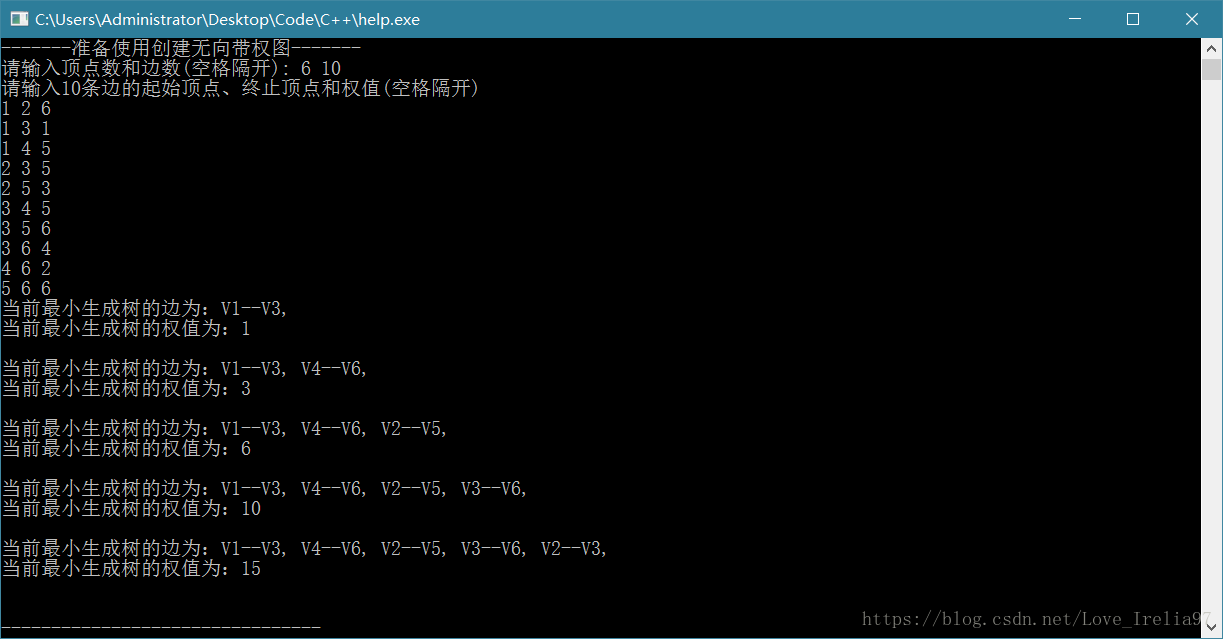
	cout << "-------准备使用创建无向带权图-------" << endl;
	cout << "请输入顶点数和边数(空格隔开): ";
	cin  >> g.vexnum >> g.arcnum;
	//	图可以没有边，但不能没有顶点
	//	若无向图有n个顶点，则最多有n*(n-1)/2条边(无向完全图) 
	if( g.vexnum<0 || g.arcnum<=0 || g.arcnum>(g.vexnum*(g.vexnum-1)/2) ){
		cerr << "数据输入有误，请检查数据！" << endl; 
		g.vexnum = g.arcnum = 0;
		return false;
	}
	
	cout << "请输入" << g.arcnum << "条边的起始顶点、终止顶点和权值(空格隔开)" << endl;
	int vstart, vend, weight;
	int n = g.arcnum;
	while( n-- ){
		cin >> vstart >> vend >> weight;
		if( vstart<=0 || vend<=vstart || weight<=0 ){
			cerr << "数据输入有误，请检查数据！" << endl;
			g.edge.clear();
			return false;	
		}
		g.edge.push_back( Edge{vstart,vend,weight} );	
	}	 
	
	return true;				
} 

void printRes(vector<Edge>& Et, int cost)
{
	cout << "当前最小生成树的边为："; 
	for(auto e : Et )
		cout << "V" + to_string(e.vstart) 
			 << "--"
			 << "V" + to_string(e.vend) << ", ";
	cout << endl << "当前最小生成树的权值为：" << cost << endl;
	cout << endl; 		
}

//	查找结点Vi的根节点 
int findRoot(int parent[], int i)
{
	int root = i;
	//	若等于，说明根为本身，已经找到 
	while( root != parent[root] )
		root = parent[root];
	return root;	
} 

bool Kruskal(Graph &g)
{
	vector<Edge> Et;	//存储目最小生成树的边 
	int cost = 0;
	//	并查集的使用，我这里定义数组下标i为顶点Vi
	//	数组的值parent[i]为顶点Vi的父节点的下标
	//	初始时Vt没有边，因此每个节点都是根节点 
	int parent[g.arcnum+1];
	for(int i = 1; i <= g.arcnum; ++i)
		parent[i] = i;
	//	将所有边的权值按照从小到大排序 
	sort(g.edge.begin(), g.edge.end(), edgeCmp);
	for(int i = 0; i < g.arcnum; ++i)
	{
		//	判断图中是否有环，使用并查集查询
		//	若该边起点，在并查集中的根节点
		//	与该边终点，在并查集中的根节点相同，则判定有环
		int root1 = findRoot(parent, g.edge[i].vstart);
		int root2 = findRoot(parent, g.edge[i].vend);
		//	不形成环 
		if( root1 != root2 ){
			//	更新权值 
			cost += g.edge[i].weight;
			//	更新并查集 
			parent[root2] = root1;
			//	更新Vt 			
			Et.push_back(g.edge[i]);
			printRes(Et, cost);
		}
		//	形成环，则忽略此边		
	}
	//	最后判断边和顶点数量关系，看是否构成了最小生成树 
	if( g.vexnum-1 != Et.size() ){
		cerr << "此图不能构造最小生成树！" << endl;
		return false; 
	} 
	
	return true;
}

int main()
{
	Graph g;
	if( newGraph(g) ){
		Kruskal(g); 
	}	
	
	return 0;
}