3.2 积分∫和 西格玛∑
虽然让人困惑,但是关于无穷大的问题是无法避免的。曾经那些放弃无穷大概念的呼声,早已被抛到九霄云外,而且永远不可能翻身。
因为如今很时髦的傅里叶变换理论已经证明,任何有限定义域的函数,其傅里叶变换后一定是无限的。物理上的波粒二象性就是这个理论的一个例子。也就是说,任何(请注意是任何)有限的东东一定伴随着一个无限的影子。
咦,真的吗?(后面会引用这个证明,其实就一句话,嘻嘻。不过要看懂这一句话,需要大量的基础知识)
可见、可触摸、可实验验证,有限的物理量是我们的支点,没错。
但如果永远停留在支点故步不前,那不是井底之蛙吗,天空的广阔需要勇气,需要大胆跳出来欣赏。如果放弃无穷的观念,最起码地,微积分何去何从?
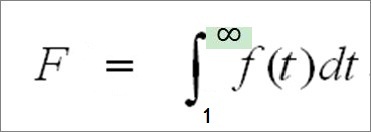
背着无穷大的微积分无处不在,无论是理科生还是文科生、无论是高中生或是大学生,都会碰到。虽然这个去了一横的f,向蚯蚓一样让人讨厌黏人。但不可否认,作为一个现代人,你无法抛弃它。因为它是现代文明的标志之一。
另一个符号西格玛,也是数学的常见符号。使用之频繁,相信每一个人都麻木漠漠、见惯不怪了。
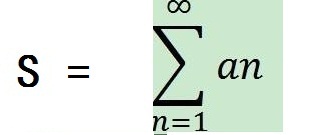
可能数学恐惧症的你不曾留意,积分∫和西格玛∑本质上是一回事,都是连加符号,都表示求和,而且都可以加到无穷。
但是,但是,但是,各位,既然都是连加求和运算,干嘛要搞出积分∫和西格玛∑两个不同的符号呢?
熟悉而陌生,曾经年少好奇的你也刨根问底想过这个问题吗?

一般老师会告诉学生,积分∫用于连续函数,西格玛∑用于离散函数。
那么连续函数和离散函数的区别又是什么呢?
区别在于:连续函数的变量是不可列的,对应的∞是‘阿列夫1’; 而离散函数的变量是可列的,对应的∞是‘阿列夫0’。
其实积分∫和西格玛∑的本质区别也在于此,在于其中的∞无穷大。
积分∫的那个∞无穷大是‘不可列的’,不可列的无穷大是‘阿列夫1’,所以积分符号的无穷是‘阿列夫1’
西格玛∑的那个∞无穷大是‘可列的’,可列的无穷大是‘阿列夫0’,所以西格玛∑符号的无穷是‘阿列夫0’
原来如此,难怪!难怪!
无穷大真的不只一个,真的有好些种呢!
醍醐灌顶、豁然开朗
《庄子.天下篇》有句名言:“一尺之捶,日取其半,万世不竭。” 意思是:一尺长的捶子,今天取其中一半,明天再取其一半的一半,后天再取其一半的一半的一半,总有一半留下,所以万世不竭。这是中国古人对无限的理解。小得意,自豪。咱们两千多年前的老祖宗,就已经毫不含糊有了数字无穷大的概念,数学圈扬眉吐气了一把。 现代知识武装过的我们知道,以这种一刀一刀砍出来小段棍子,其实就是一个有理数的数列,是一列有理数,因而有理数是可列可数的,有理数的全体构成了一种无穷大,即‘阿列夫0’。自然数的的通常理论中,皮亚诺算术公理系统从n+1维递归到无穷维度,这个参照系是一个离散无穷维空间(阿列夫0维度线性空间)。
文艺复兴之后,古希腊的思想在欧洲如雨后春笋生根发芽。有幸一览古希腊内功心法秘籍《几何原本》的牛顿同学,终成一代大侠,创立了微积分。微积分把无穷大的级别由阿列夫0版升级到阿列夫1版。人类的视野从此上升到一个崭新高度。后来,数学大师希尔伯特又进一步引入连续谱分析的理念,将微积分和线性代数合而为一,创造了连续无穷维希尔伯特空间(阿列夫1维度线性空间),为量子矩阵力学开辟了前所未有的广阔沃土。
我们已经知道,阿列夫0是无穷大家族中最小的一个。虽然同是无穷大,但阿列夫0比阿列夫1小得多,到底小到什么程度呢?
康托尔老师告诉我们,‘离散’的阿列夫0 和‘稠密’的阿列夫1比较,不过是沧海一粟、微不足道。 哪怕取很小很小的一小段连续实数中的无理数(即阿列夫1),
【比如从0到0.0000000000000000000000000000000…1中那么一丁点儿小段】,也比所有的有理数全体(即阿列夫0)大得多得多!!!!!!
啊,啊,啊!
一句话惊醒我梦中人
借此, 顺便提下物理学两个著名的公式(瑞利-金斯公式)、(普朗克公式):


看见了吗? 这两个公式基础形式几乎一模一样,只不过一个积分∫表达式,另一个是西格玛∑表达式。
但是,就这点区别,一个导致了经典物理“紫外灾难”的乌云(瑞利-金斯公式),另一个是开创全新的量子时代的金钥匙(普朗克公式)。