22. 采用最大似然估计的方法，求出逻辑回归算法的损失函数

参数求解

样本概率

根据之前的介绍，我们可以将类别y（1与0）的概率表示如下（这里使用s代表sigmoid函数）：
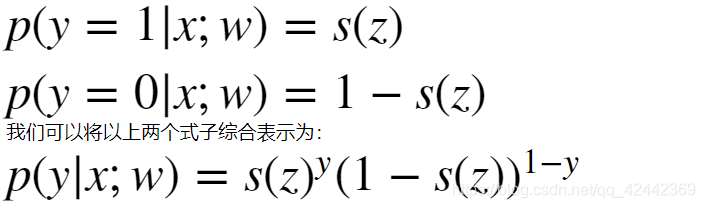
在这里插入图片描述
我们可以将以上两个式子综合表示为：

$p(y|x;w) = s(z)^y(1 - s(z))^{1-y}$

最大似然估计

以上是一个样本的概率，我们要求解能够使所有样本联合密度最大的w值，因此，根据极大似然估计，所有样本的联合概率密度函数（即似然函数）为：

$L(w) = \prod_{i=1}^{m}p(y^{(i)}|x^{(i)};w)\\ = \prod_{i=1}^{m}s(z^{(i)})^{y^{(i)}}(1 - s(z^{(i)}))^{1-y^{(i)}}$

为了方便求解，我们取对数似然函数，让累计乘积变成累计求和：
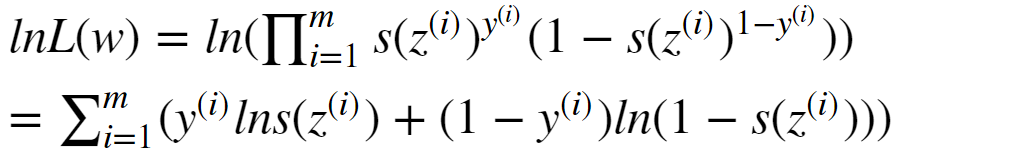
在这里插入图片描述
我们要使得上式的值最大，可以采用梯度上升的方式。不过，这里我们为了引入损失函数的概念，我们采用相反的方式，即只需要使得该值的相反数最小即可，因此，我们可以将上式的相反数作为逻辑回归的损失函数（交叉熵损失函数）：
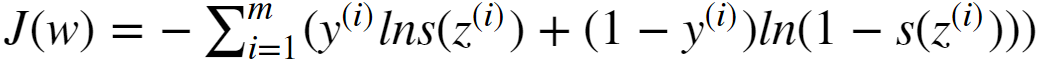
在这里插入图片描述

交叉熵损失函数分析

为了方便起见，我们可以对单个样本进行分析。由损失函数的组成，我们可以得出：
1. 当真实类别为1时，sigmoid函数（可以认为是得分预测函数）的值越接近于1，则损失值越小。
2. 当真实类别为0时，sigmoid函数的值越接近于0，则损失值越小。
我们现在来绘制损失函数曲线。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"] = False

s = np.linspace(0.01, 0.99, 200)
for y in [0, 1]:
    # 逻辑回归的损失函数。
    loss = -y * np.log(s)-(1 - y) * np.log(1 - s)
    plt.plot(s, loss, label=f"y={y}")
plt.legend()
plt.xlabel("sigmoid(z)")
plt.ylabel("J(w)")
plt.title("损失函数J(w)与sigmoid(z)的关系")
plt.show()

在这里插入图片描述

梯度下降求解

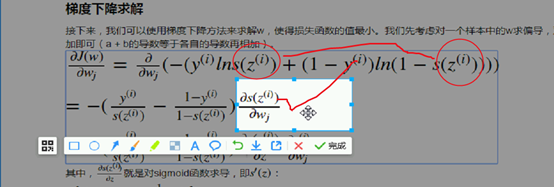
接下来，我们可以使用梯度下降方法来求解w，使得损失函数的值最小。我们先考虑对一个样本中的w求偏导，对于所有样本，只需要依次将所有样本的偏导结果累加即可（a + b的导数等于各自的导数再相加）。
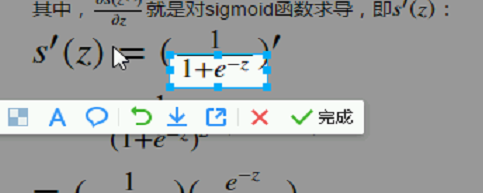
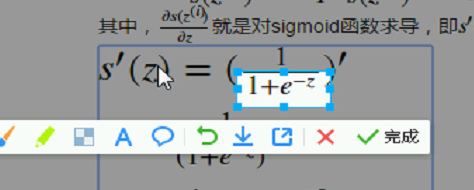
在这里插入图片描述
其中， $\frac{\partial s(z^{(i)})}{\partial z}$ 就是对sigmoid函数求导，即 $s'(z)$ ：

因此，上式为：

进一步解释公式的推导过程

如何得到？
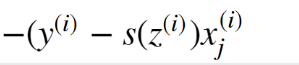
在这里插入图片描述
以x w作为参数的时候 y=1 的概率是多少？
s(z)是sigmoid 的简写。
y=0 就是 1 – s(z)

s越大 y=1 的p越大
s越小 y=0 的 p越大

以x作为前提，w为参数，也就是条件概率。
然后将两个式子合并在一起，因为方便计算。
看 y=1 带入 s(z)；y=0 带入 1-s(z)，这样两个式子就统一了。
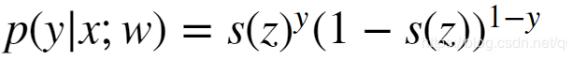
在这里插入图片描述
把这两个概率综合在一起考虑了，一个样本有一个z的值，任何一个样本的概率值是多少？目的就是让这个联合概率最大。

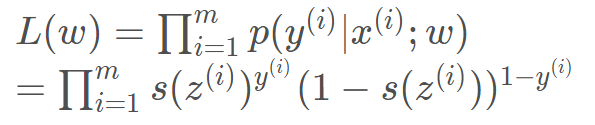
不知道概率相关的参数，但有结果，让结果最大，推参数。
使用最大似然估计，进行累乘，估计w的值。
带入，还是一个累乘的形式，不方便，考虑在似然函数上取对数，函数虽然变了，但没关系，不改变极值点。之前的博文也提到过。

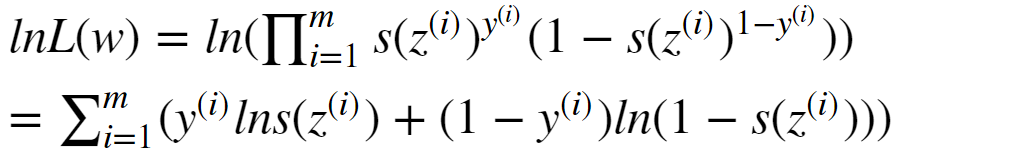
在这里插入图片描述
得到上面式子的过程需要用到的对数公式知识：

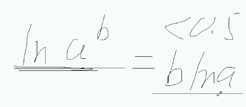
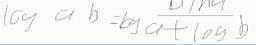
让它达到最大，本来应该用梯度上升，但梯度上升在机器学习中一般不用；解决方法：加上符号。

所以目的就是让下面的式子最小，求w：
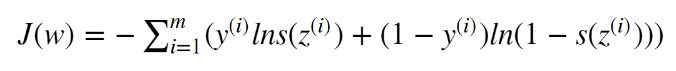
在这里插入图片描述
交叉熵损失函数：

类别 * ln类别（一个类别，另一个类别）
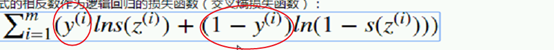
在这里插入图片描述

Why 分类算法用交叉熵？，而回归用平方和比较合适？**

在回归算法中，真实100 预测 50 90 它们损失不一样，但是分类当中上述的不合适。

而在分类算法分 1 2 3 4 5类别，1是正确的，除非你预测是1 ，否则其他都是错的，预测2 越策5 都是错的，都是一样的，不在乎哪一个编一个好，也没有接不接近的说法，不是特别合适。

why用交叉熵类别乘以 ln类别 ,而不会出现平方和的问题?

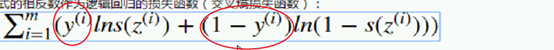
在这里插入图片描述
观察，分析：
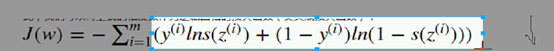让它越来越大；当y是1 后买是0

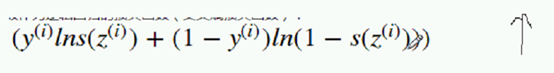
让它越大越好，前面是1

让ln越大越好；就是让 z sigmoid越大越好

S(z)最大也就是能取到1 因为 e^0 等1
在这里插入图片描述
当yi 取1 的时候，我们希望sz越大越好，就代表越趋紧真实的1
Sz越小小小加符号越来越大

如果yi要是0，
只剩下这个部分：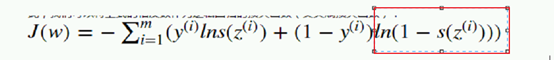
希望它越大越好，就是希望：

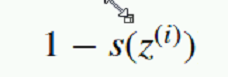
在这里插入图片描述
越大越好，也就是s(z)月小越好

逻辑回归的损失函数隆重推出：

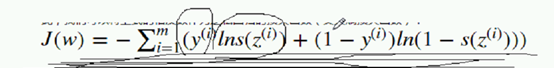
交叉熵损失函数代码中，y取0的时候循环一次，1的时候循环一次。

在这里插入图片描述
不取0，取0.01，因为log 不能取0；
不能取1，取0.99 ，因为1-1=0了。

在这里插入图片描述

y=1 sz增大越趋近于1 损失函数越小；
也符合实际，sz越大，信心指数越强，真实值又是1。

y=0 sz增大损失值上涨;
真实类别为0 预测为1的信心指数越强预测差距越大损失函数的值越大。

不用复杂方法，简单看损失函数：

能快速分析出上面的结论：
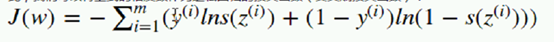
在这里插入图片描述
真实类别 y=1；只剩下 -lins(z(i))
zg越大损失函数越小，就可以采用梯度下降求；
求偏导，先只求一个样本然后再累积求和。后续…

wj在哪儿 z里面；其中多处涉及复合函数求导：

首先看 ln A ; Lna导数 1/a
在这里插入图片描述

提出来都涉及szi对wj求偏导提到外面。

在这里插入图片描述
下图又是一个复合函数

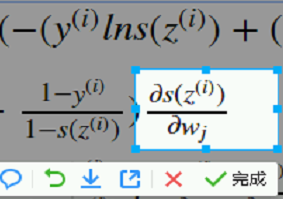
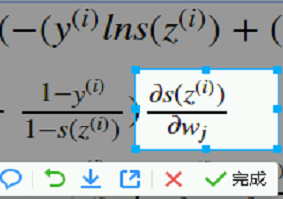
对里面的求导，sigmoid z 求偏导直接写出

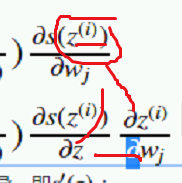
所以对他求导数，又是一个复合函数

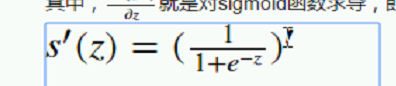
导数

大A

A的-1等于，-a的平方之一

里面的大A，复合函数求导；e的a次方求导还是：

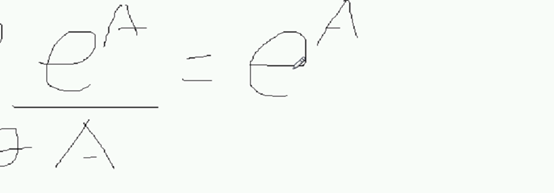
A对z求偏导：
在这里插入图片描述
A就是-z；所以就是：

进行整理：
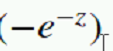上去；然后拆开；平方拆两个

得到：

符号抵消了；然后改种写法一样的：

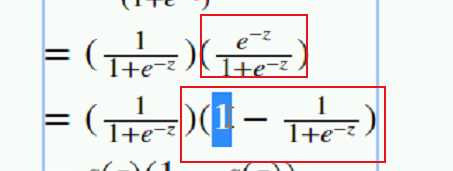
在这里插入图片描述
得到然后根据：

xj提到外面；撑开:

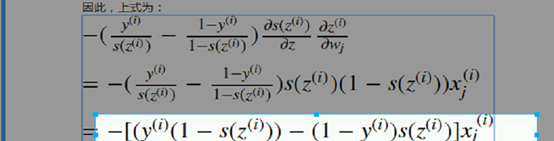
Yi -yi *szi -

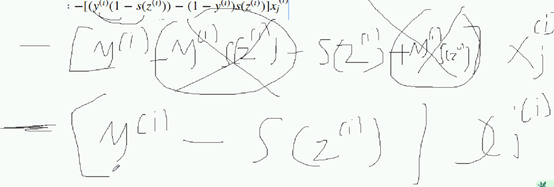
到了梯度下降的更新公式

szi就是simgoi的；开始更新；梯度值乘以eta。
-梯度值前面有符号负负为正原本是减号。
得到这个公式：

批量的话，所有样本加载一起搞；不断迭代就能让损失函数越来越小；求出w值。
挺相似的只不过是概率的预测换成y_hat：
在这里插入图片描述
接着再循环里面不断的迭代就可以了。