点的旋转（1）：二维平面及复数

版权声明：, https://blog.csdn.net/u011760195/article/details/85321280

前言

在阅读本文之前，你应该对笛卡尔坐标系和复数有一定了解，我们将从复数的角度来解释旋转。
不过在这之前我们先来看看加法和乘法的另一种思想

加法

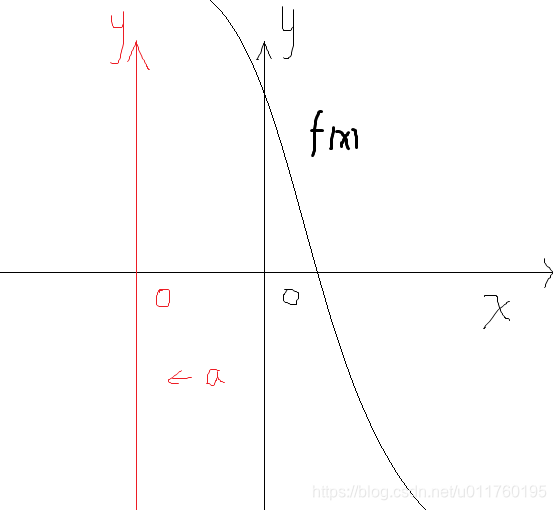
在二维平面，你一定学习过函数f(x) 的左右平移变换。

你是不是第一时间想到了“左加右减”？

假设我们使 f(x)向右移动a个单位，并将移动后的函数称为：f(t)
则有 $f(x) = f(t+a)$
$x = t+a$
$t = x-a$
求得变换后函数f(t) = f(x-a)
或许你一时间可能不是很明白这个转换的过程，让我们换个说法。

我们并不移动函数f(x)，我们移动坐标轴x。
根据物理上的相对运动，当我们想右移f(x)时可左移x轴。

这样，f(x)所有点的x轴长度都增加了a
要求新坐标轴下的点，我们需要将新x减a，变换成原坐标系下的点来求函数的值，也就是f(x-a)
是的，这样一种滑动坐标轴的思想就是我们的加法新思想。
上例中，我们称a为加子。
下面我们来看看乘法

乘法

2*3 = 6，很轻易就能算出来

但是你们是如何思考这个乘法过程的呢？
2+2+....+2
一共有3个2相加

现在让我们换一种思想
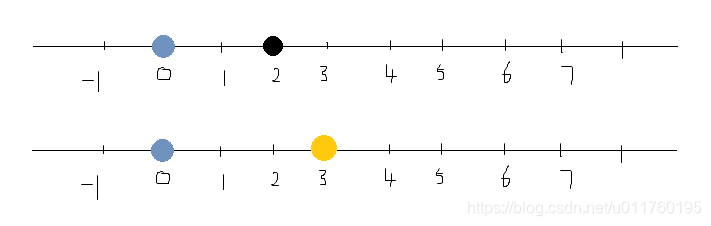
我们把2，3放在数轴上来考虑

我们分别将1，2数轴看作数字2，3
我们将乘法看成是一种缩放操作

我们将3称为乘子，以O点为缩放原点，将代表2的数轴上的点1缩放至乘子的位置

并根据单位重新刻度，原来数轴上2的位置的值即是乘法结果： 6
那么如果是2*(-3)呢？
下面就是重轴戏。

复平面

复数的定义： $a+bi$
其中 $i^2 = -1$
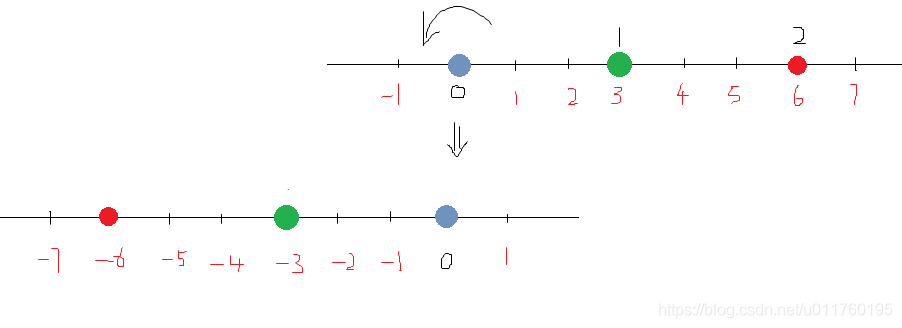
让我们回到 2*(-3)的问题上
我们可以将其变成这种形式： $2 * 3i^2$
$2 * (3i^2 + 0i)$
虚部为零，导致了乘法结果并没有偏离实轴，让我们进一步变换
$2 * { (0 + 3i)*(0 + i)}$
让我们再来看看上面的 2*3
$2 * (3 + 0i)$
$i^2 * i^2 = 1$
$2 * (3i^4 + 0i)$
$2 * (0+3i)*(0 + i)*(0 + i)*(0 + i)$

你发现了什么？
这看起来，好像2*(-3)少了两次乘子(0 + i)的操作，而缺少这两次乘子导致其落在了数轴的另一侧。
不难想象：两次乘子(0 + i)对应一次数轴的180度旋转。
那么一次(0 + i)就对应了90度的旋转，这也可以解释为什么 $i^2 = -1$

于是，2*(-3)可以变换成
$2*3*(0+i)*(0+i)$
只需将2*3的结果数轴旋转180度再重新刻度便是最终答案

在旋转的过程中数轴滑过的空间，便是这个维度的复数空间
下面我们就以复数为乘子来研究二维平面的旋转

旋转

上例中，我们的乘子是a+bi中的一种特殊情况
现在我们看看更一般的情况：

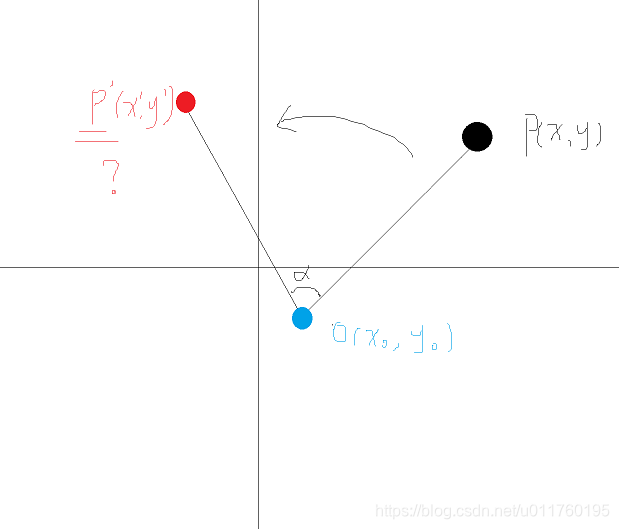
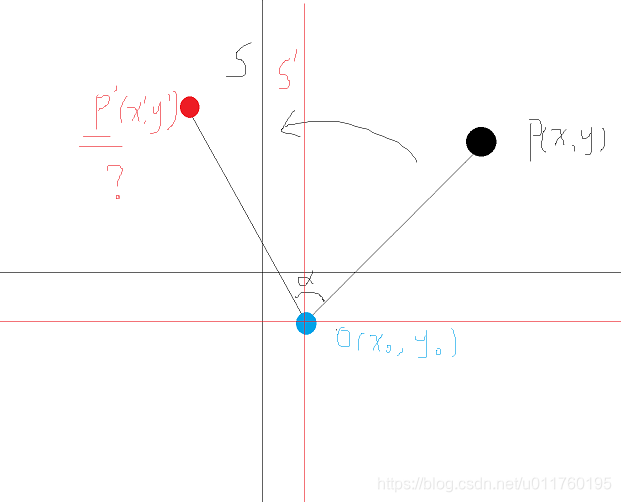
P(x,y)，O(x_o,y_o)，逆时针旋转α度，结果点P’(x’,y’)
我们将其转化为复平面上的旋转
我们将坐标系的x轴右移x_o，y轴上移y_o得到坐标系s’

在系s’下，问题变得很简单
旋转α度，仅需乘上一个乘子r $r = (a+bi)$

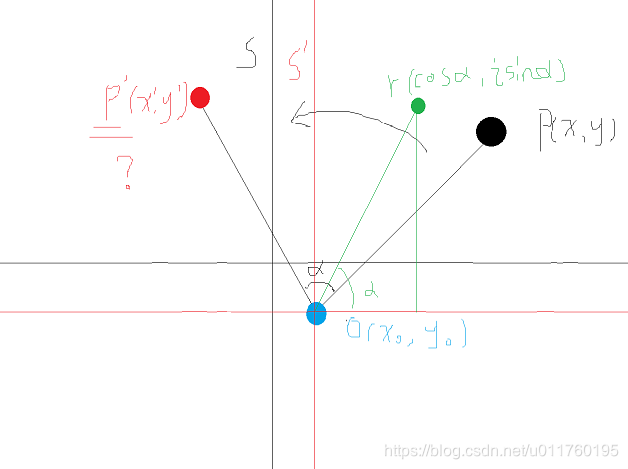
这个乘子对应一个旋转操作，也就是

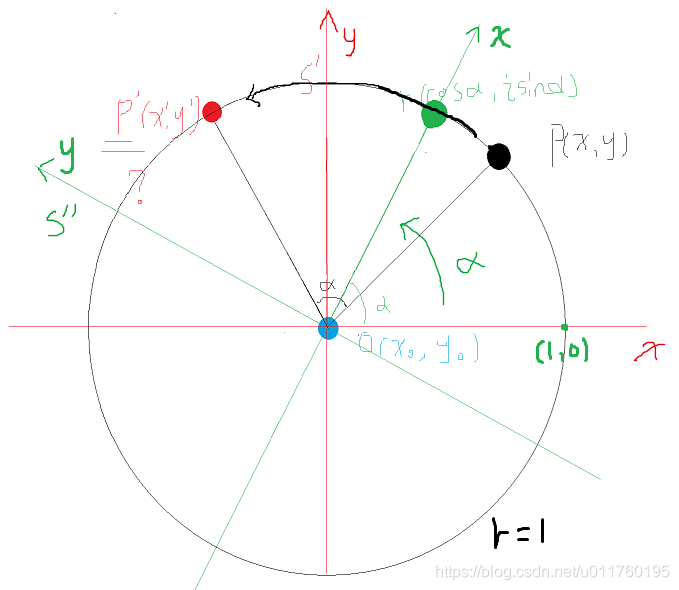
将s’中的(1+0i)点变换到乘子r所在的位置
我们将p所在的系s’通过乘子r来旋转，得到变换后的系s’’，便是p*r的结果
这个乘子的模为1（1是确保本次操作仅仅旋转，不会改变p的模长），辐角为α，不难推导
$a = cosα , b = sinα$
于是
$r = (cosα + isinα)$
$p' = p*r$
即：
$(x'_s+y'_si) = (x_s+y_si)*(cosα + isinα)$
而此时p及p’的x轴坐标减少了x_o，y轴坐标减少了y_o
即：
$x_s = x -x_o,y_s = y -y_o$
$x'_s = x' -x_o,y'_s = y' -y_o$
$(x' -x_o+(y' -y_o)i) = (x -x_o+(y -y_o)i)*(cosα + isinα)$
也就是：
$x'=x_o + (x-x_o)cosα-(y-y_o)sinα$
$y'=y_o + (x-x_o)sinα+(y-y_o)cosα$

至此，二维平面上点的旋转已经推导完毕，在后面的部分，我们将探索三维空间的旋转，以及复数的扩展 —— 四元数