【题10 斐波那契数列】

算法和数据操作
• 递归和循环：
很多算法可以用递归和循环两种不同方式实现。
通常基于递归的实现方法代码会比较简洁，但性能不如基于循环的实现方法。
• 排序和查找：
重点掌握二分查找，归并排序和快速排序。
例题11旋转数组的最小数字
• 回溯法：
要求在二维数组（迷宫或棋盘）上搜索路径用回溯法。
通常回溯法很适合用递归的代码实现。
如果限定不可以用递归，考虑用栈来模拟。
【题12矩阵中的路径，13 机器人的运动范围】
• 动态规划：
求某个问题的最优解，并且该问题可以分为多个子问题。
用自上而下的递归思路去分析动态规划问题的时候，会发现子问题之间存在重叠的更小的子问题。
为了避免重复计算，用自下而上的循环代码实现，把子问题的最优解先算出来并用数组（一维或者二维）保存下来，接下来基于子问题的解计算大问题的解。
• 贪婪算法：
动态规划的思路后，还在提醒在分解子问题的时候是不是存在某个特殊的选择，如果采用这个特殊的选择将一定能得到最优解，那么采用贪婪算法。
【题14 剪绳子】
• 位运算：
一类特殊的算法，把数字表示成二进制之后对0和1的操作。由于位运算的对象为二进制数字，所以不是很直观，
共有与，或，异或，左移和右移5种运算。
【题15 二进制中1的个数】

递归和循环
递归是在一个函数的内部调用这个函数自身。
循环是通过设置计算的初始值和终止条件，在一个范围内重复计算。
递归优点：简洁
递归缺点：
（1）由于是函数调用自身，函数调用是由时间和空间消耗的。
（2）很多计算时重复的，对性能带来负面影响。
（3）栈溢出：函数调用在栈中分配空间，而每个进程的栈的容量时有限的，当递归调用的层级太多时，就会超出栈的容量，导致栈溢出。
【题10 斐波那契数列】
【题目一】
写一个函数，输入n，求斐波那契（Fibonacci）数列的第n项，斐波那契数列的定义如下
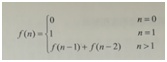
在这里插入图片描述
<效率很低的解法，不喜欢>

评价：
这种解法存在效率问题。这棵树中有很多节点是重复的，而且重复的节点会随着n的增大而急剧增加，这意味着计算量会随着n的增大而急剧增大。用递归方法计算的时间复杂度是以n的指数的方式递增的。

<期待的实用解法：避免重复计算>
从下往上计算
（1）首先根据f(0)和f(1)计算出f(2),
（2）再根据f(1)和f(2)计算f(3)
……
依次类推算出第n项了。时间复杂度为O(n)

<时间复杂度O(logn)，但不够实用的解法>
数学公式：（可以用数学归纳法证明）
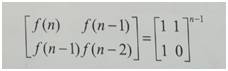
在这里插入图片描述
有了这个公式，只需求得矩阵

即得到f(n)
现在问题转成如何求矩阵

的乘方。
考虑乘方的性质。

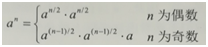
想求n次方，就要先求得n/2次方，再把n/2次方的结果平方一下即可。递归实现。

实现

package ti10;

/**
 * 剑指offer面试题9：斐波那契数列
 * 题目：写一个函数，输入n，求斐波那契数列的第n项。
 * 　　　　　　　　　　　　　　　　　　　　0,                n=1
 *     斐波那契数列定义如下：f(n)=      1,                n=2
 *                              　　 f(n-1)+f(n-2),    n>2

 */
public class No9Fibonacci {

    public static void main(String[] args) {
        System.out.println("第4项斐波那契数列的值为："+fibonacci(4));
    }

    /*
     * 采用递归实现斐波那契数列生成函数，效率低
     */
    public static int generateFibonacci(int n){
        if(n==0)
            return 0;
        if(n==1)
            return 1;
        return generateFibonacci(n-1)+generateFibonacci(n-2);
    }
    
    /*
     * 采用循环实现斐波那契数列
     * 存储数列中间项，求得结果
     */
    public static int fibonacci(int n){
        int[] result={0,1};
        if(n<2)
            return result[n];
        int fibNMinusOne=1;
        int fibNMinusTwo=0;
        int fibN=0;
        for(int i=2;i<=n;i++){
            fibN=fibNMinusOne+fibNMinusTwo;
            fibNMinusTwo=fibNMinusOne;
            fibNMinusOne=fibN;
        }
        return fibN;
    }
}

解法比较：
法一：基于递归的解法：直观，但时间效率很低。实际软件开发中不会用这种方法。
法二：把递归算法用循环实现：极大提高了时间效率。
法三：把求斐波那契数列转换成求矩阵的乘方。可以用O(logn)求得矩阵的n次方，但由于隐含时间常数较大，很少有软件采用这种方法。

【题目二：青蛙跳台阶问题】
一只青蛙依次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个n级台阶总共有多少种跳法。
分析：
（1）考虑最简单情况：
如果只有1级台阶，显然一种跳法
如果只有2级台阶，有两种跳法1.分两次跳，每次1级。 2．一次两级
（2）一般情况：
把 n级台阶时跳法看成n的函数，记为f(n).
当n>2时，第一次跳的时候有两种不同选择：
1.第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目f(n-1)
2.第一次跳2级，此时跳法数目等于后面剩下的n-2级台阶跳法数目，即为f(n-2)
因此，n级台阶的不同跳法的总数为f(n)=f(n-1)+f(n-2)

实现

package ti10;

public class P77_FrogJumpFloor {
    public int FrogJumpFloor(int target) {
        int result = 0;
        if (target == 2 || target == 1) {
             result = target;
        }
        int temp1 = 1;
        int temp2 = 2;

        for (int i = 3; i <= target; i++) {
            result = temp1 + temp2;
            temp1 = temp2;
            temp2 = result;
        }
        return result;
    }
    public static void main(String[] args) {
        int n = 2;
        P77_FrogJumpFloor test = new P77_FrogJumpFloor();
        int result = test.FrogJumpFloor(n);
        System.out.print(result);
    }
}

【扩展】
在青蛙跳台阶问题中，如果把条件改成：一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级，此时该青蛙跳上一个n级台阶总共有多少种跳法？
数学归纳法可以证明f(n)=2^(n-1)
分析
假设f(n)是n个台阶跳的次数。

f(1) = 1
f(2) 会有两个跳得方式，一次1阶或者2阶，这回归到了问题f(1),f(2) = f(2-1) + f(2-2)
f(3) 会有三种跳得方式，1阶、2阶、3阶，那么就是第一次跳出1阶后面剩下：f(3-1);第一次跳出2阶，剩下f(3-2)；第一次3阶，那么剩下f(3-3).因此结论是f(3) 会有三种跳得方式，1阶、2阶、3阶，那么就是第一次跳出1阶后面剩下：f(3-1);第一次跳出2阶，剩下f(3-2)；第一次3阶，那么剩下f(3-3).因此结论是
f(3) = f(3-1)+f(3-2)+f(3-3)
f(n)时，会有n中跳的方式，1阶、2阶…n阶
得出结论：
f(n) = f(n-1)+f(n-2)+…+f(n-(n-1)) + f(n-n)
f(0) + f(1) + f(2) + f(3) + … + f(n-1) == f(n) = 2f(n-1)
即f(n) = 2f(n-1)

每个台阶都有跳与不跳两种情况（除了最后一个台阶），最后一个台阶必须跳。所以共用2^(n-1)中情况

实现

package ti10;

public class Solution {
    public int JumpFloorII(int target) {
        int result=0;
        if(target==0)
        {result=0;
        }else if(target==1)
        {result=1;
        }else{
            result=2*JumpFloorII(target-1);
        }
        
      return result; 
     
    }
    public static void main(String[] args) {
        int n = 5;
        Solution test = new Solution();
        int result = test.JumpFloorII(n);
        System.out.print(result);
    }

}

【相关题目】
我们可以用21（左图）的小矩形横着或者竖着去覆盖更大的矩形，请问用8个21的小矩形无重叠地覆盖一个2*8的大矩形（右图）总共有多少种方法？
在这里插入图片描述

把2 * 8的覆盖方法即为f(8)
第一个2 * 1的小矩形去覆盖大矩形最左边时有两种选择：竖着放，横着放。
竖着放时，右边剩下2 * 7区域，覆盖方法记为f(7)
横着放时，当小矩形横着放在左上角时，左下角必须放一个，
右边还剩2 * 6，覆盖方法记为f(6)
因此f(8)=f(7)+f(6).

参考：
1.《剑指offer》
2.https://www.cnblogs.com/gl-developer/p/6445445.html
3.https://blog.csdn.net/Sunshine_liang1/article/details/82468306
4.https://blog.csdn.net/xiaomei920528/article/details/74178927

【题10 斐波那契数列】

猜你喜欢