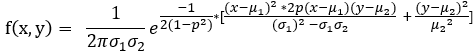概率论：
随机事件： 包括基本事件，复合事件，必然事件，不可能事件；
A⊆B： 事件A 发生，一定导致事件B 发生；
A=B： A⊆B, B⊆A
A∪B: 事件A与事件B 至少发生一次；
A∩B,AB,A*B: 事件A 与 事件B 同时发生；
AB=∅时，则事件A 与 事件B 为互斥事件(互不相容事件)；
A-B = A- A∩B = A
AB=∅,且 A∪B =S, 则 事件A 与 事件B 互为逆事件，或 对立事件；
逻辑分配律： A∪(B∩C) = (A∪B)∩(A∪C);
德摩根率：
= 
= 
= 
概率公理：
1.非负性；
2.概率的有限可加性；
3.性质：
1. A⊆B,则 P(B) >= P(A), 且 ： P(A-B)=P(B)-P(A);
2. 0<=P<=1, P(A)+ P(
) = 1;
3. P(A∪B)<= P(A)+P(B);
P(A∪B) =P(A)+P(B)-P(AB)
古典概型：
特点：
1.样本元素有限；
2.每个基本事件出现的可能性相等；
公式：
A称为： 排列数公式；
C称为： 组合数公式；
关于排列组合的自我理解！ 结合这里: 组合数公式= 排列集合 去掉 重复的组合；
条件概型：
, 表示 在A发生的情况下，B发生的概率；
若 
， 则 
乘法公式:
P(AB) = P(A)*P(B|A)
推广： 将一部分看作为整体，依次拆开；
注意条件概率，与同时出现的区别；
全概率公式:
由乘法公式 和 条件概率 推导而来；
贝叶斯公式：
全概率公式的升级；
，可看作由条件概率推导而来；
独立事件：
P(A|B) = P(A) =P(B|A);
有： P(AB) = P(A)*P(B);
相互独立与互不相容的区别:
互不相容，指的是不能同时发生；
相互独立，指的是二者可以同时发生，只是两个事件互不影响；
二者没有关系，或者说没有推理关系；
ABC三事件两两独立 =/= 三事件独立；
若AB为独立事件，则A与B，A与
， 
与
也相互独立；
随机变量：
分类： 离散型； 非离散型(连续型，其它)；
随机变量的分布律：
随机变量X 所有可能取值的概率情况表示为:
表示：随机变量X服从该分布；
或者记作：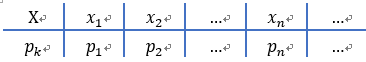 
一般地，概率有三种表达式：
1.分析表达式： 如：
2.表格或者 矩阵表达式，如上；
3.图形表达式；
常见离散型随机变量的概率分布：
1.两点分布：
即 X 只可能取 0 和 去两个值，其表达式为：
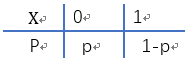
2.等可能分布：
即 X 的分布 服从：
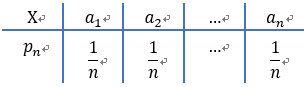
3.二项分布:（n重伯努利实验： 相互独立实验n重，只有两种可能结果）
记作： 
泛化：
或者表示为： 
或者记作： X ~ b(n,p)
4.泊松分布:
泊松定理：设 λ是一个大于0 的常数， n 为正整数，若 有： 
,则 对任意正整数k , 有：
记作： 
5.几何分布：
其中，p=1-q, q表失败，p表成功。
随机变量的分布函数：
理解： 分布函数存在的原因在于，级数的知识让我们知道累加的式子存在规律；
分布函数概念：
对于随机变量X，我们不仅要知道X取哪些值，知道X取这些值的概率，更重要的是想知道X在 区间(a,b)的概率；
eg: 
，记
，
分布函数的定义：
设X 是随机变量，x 是任意实数，函数 F(x) = P{X<= x},称为 X 的分布函数；
它的定义域为： R , 值域为： [0,1]
注意： P{X >= 5.5} 与 P{x >= 5.5}是不一样的。
分布函数的性质：
1. 0 <= F(x) <= 1, x∈(-∞,+∞);
2. F(x1) < F(x2), (x1 < x2)
3. F(-∞) = lim F(x)= 0, x-> -∞;
F(∞) = lim F(x) =1, x-> ∞;
4. 
分布函数重要公式:
1. P{a<= X <= b} = F(b) - F(a);
2. P{X > a} = 1-F(a);
注意，不同的随机变量，其分布函数不一定不同
连续型随机变量及其概率密度：
几何概型： 若事件发生的概率 只与 长度（或面积，或体积）有关，则称之为 几何概型；
连续性随机变量：
对于 X 的分布函数 F(x), 存在非负函数，使得 ∀ x∈R,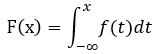 
(边上限积分), f(x) 称为 x的概率密度函数；称X 为连续性随机变量；
性质:
F'(x) = f(x)
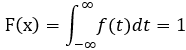
概率密度 和分布函数 必知 其一 方可求解；
概率密度的概念与性质：
对于随机变量X，对于分布函数F(x),存在非负函数，对∀ x∈R,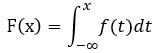 
,称为：X 为连续性随机变量； f(x)称为 X 的概率密度函数；
性质:
1. f(x) >= 0;
2. P{X <= a} = F(a) = 
3. 若 P{x=a} =0, 此时 无法确定 {X = a} 是不可能事件；
4. P{X >a} = 1-F(a) = 
5. 若 f(x) 在 点 x 处连续，则有 F'(x) = f(x) 即 可积分函数的原函数一定连续；
eg: 设连续性随机变量X 的分布函数：
F（x）=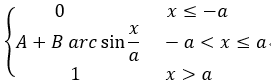 
1.求 A,B的值； 2.求X的概率密度函数；
eg: 设 随机变量 X 的概率密度：
f(x) =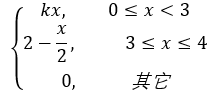
1.求k； 2.求 X 的分布函数；
常见连续型随机变量的分布（概率密度函数 与 分布函数）：
1.均匀分布：
概率密度：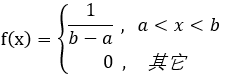 
, 称X 服从区间(a,b) 的均匀分布； 记作： X ~ U(a,b)
分布函数：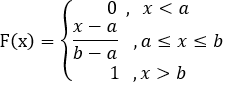 
2.指数分布：
概率密度： 
, 称 X 服从 指数分布； 记作： X ~ Z(α);
分布函数： 
3.正态分布（高斯分布）：
概率密度：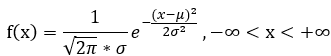 
,
称 X 服从参数为 μ 和 σ^2 的正态分布，记作: X ~N(μ,σ^2);
其中参数的作用： μ 改变概率密度函数图像的位置，称为位置参数； σ影响概率密度函数图形的峰高，称为尺度参数；
分布函数：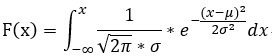 
标准正态分布： 若 X ~（0，1） 则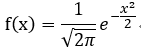 
称为标准正态分布；
性质： 其概率密度图像关于 x= μ 对称，因此有：
f(x) =f(2μ -x) ==> F(x) = 1-F(2μ-x) = 1-F(-x)
注意，其分布函数不一定对称；
若函数的原函数不为初等函数，则可以用二重积分计算其定积分的值。
常见标准正态分布值： Φ(0) =0.5 ,Φ(0.5) = 0.6915
引理（正态分布的标准化）：
若 X ~N(μ,σ^2), 则 Z = （x-μ)/σ ~ N(0,1)
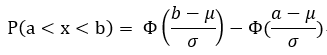, 即 所有分布都可以转化为标准正态分布计算；
随机变量的函数分布(跟 连续性随机变量的概率密度函数，以及离散型随机变量的概率分布 不是同一个概念)：
以下内容引用自：当地较为英俊的男子
所以，随机变量的分布函数也好，随机变量的函数分布也好， 它们的本质 都是分布函数。 断句时要注意，并且要注意全称： 随机变量 的 分布函数 以及 随机变量的函数 的 分布函数；
如： Y = sin X;
1.离散型： 略；
2.连续性随机变量的函数分布：
1.分布函数法:
即 先求 
分布函数，再求： 
= 
;
2.公式法：
多维随机变量及其分布：
二维随机变量：
设 E 是随机实验，样本空间 S ={w} , 设 X = X(w) , Y = Y(w) 是定义在S 上的 随机变量， 由他们构成的一个向量(X,Y) 叫二维随机变量； 记作： (X,Y) = （ X(w) , Y(w)）;
二维随机变量的联合分布函数：
称为 随机变量 X 和 Y 的 联合分布函数；
若 
，称为 边缘分布函数；
性质：
1. F(x,y) 是 变量x 和 y 的不减函数，即对于任意固定的 y， 当 x2>x1 时，F(x2,y) >= F(x1,y);
2. 0 <= F(x,y) <= 1 且 有
对于任意固定的 y,
F(-∞，y) = lim F(x,y) =0 , x-> -∞;
F(-∞,-∞) =0;
F(+∞,+∞)=1;
3. F(x,y) = F(x+0,y) , F(x,y) = F(x,y+0);
二维随机变量的分布函数性质：
F(x1 < X < x2 , y1 < Y < y2) = F(x2,y2) - F(x1,y2) -F(x2,y1) + F(x1,y1);
边缘分布函数： 
二维离散型随机变量：
分布概率： 
性质：
1. P ij >= 0;
2. 
;
分布函数： F(x,y) = P{X <= x , Y <= y};
边缘分布 概率：
, 即当 x 或 y 一方不变时，对应的x 或者 y 加满。
边缘分布函数： 
二维连续性随机变量：
分布函数： 
, 其中，f(u,v) 为概率密度函数；
性质：
1. f(x,y) >= 0, -∞<x <+∞;
2 .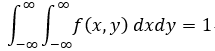 
3. 
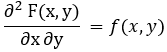, 其说明：分布函数 F(x,y) 与 密度函数 f(x,y) 可相互确定。
4. 随机点 (X,Y) 落在平面的概率：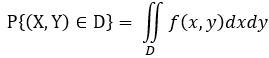 
边缘概率密度 以及 边缘分布函数：
<1>. 知 F(x,y) , 求 
边缘分布函数： 
<2>. 知 F(x,y) 求 
先求，再求：
<3>. 知 f(x,y) , 求
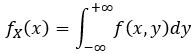
<4>. 知 f(x,y) , 求 F(x,y)
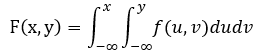
<5>. 知 f(x,y) ，求：
关键式子：
二维随机变量的常用分布：
1.均匀分布：
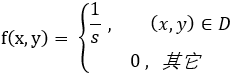
2. 二维正态分布：
