「学习笔记」反向传播Back Propagation

BackPropagation算法是多层神经网络的训练中举足轻重的算法。

简单的理解，它的确就是复合函数的链式法则，但其在实际运算中的意义比链式法则要大的多。

背景知识

简单表达式和理解梯度

从简单表达式入手可以为复杂表达式打好符号和规则基础。先考虑一个简单的二元乘法函数 $f(x,y)=xy$ 。对两个输入变量分别求偏导数还是很简单的：

$\displaystyle f(x,y)=xy \to \frac {df}{dx}=y \quad \frac {df}{dy}=x$

导数的意义：函数变量在某个点周围的极小区域内变化，而导数就是变量变化导致的函数在该方向上的变化率。

$\frac{df(x)}{dx}= lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

注意等号左边的分号和等号右边的分号不同，不是代表分数。相反，这个符号表示操作符 $\frac{d}{dx}$ 被应用于函数 $f$ ，并返回一个不同的函数（导数）。对于上述公式，可以认为 $h$ 值非常小，函数可以被一条直线近似，而导数就是这条直线的斜率。换句话说，每个变量的导数指明了整个表达式对于该变量的值的敏感程度。比如，若 $x=4,y=-3$ ，则 $f(x,y)=-12$ ， $x$ 的导数 $\frac{\partial f}{\partial x}=-3$ 。这就说明如果将变量 $x$ 的值变大一点，整个表达式的值就会变小（原因在于负号），而且变小的量是 $x$ 变大的量的三倍。通过重新排列公式可以看到这一点（ $f(x+h)=f(x)+h \frac{df(x)}{dx}$ ）。同样，因为 $\frac{\partial f}{\partial y}=4$ ，可以知道如果将 $y$ 的值增加 $h$ ，那么函数的输出也将增加（原因在于正号），且增加量是 $4h$ 。

函数关于每个变量的导数指明了整个表达式对于该变量的敏感程度。

如上所述，梯度 $\nabla f$ 是偏导数的向量，所以有 $\nabla f(x)=[\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}]=[y,x]$ 。即使是梯度实际上是一个向量，仍然通常使用类似“x上的梯度”的术语，而不是使用如“x的偏导数”的正确说法，原因是因为前者说起来简单。

我们也可以对加法操作求导：

$\displaystyle f(x,y)=x+y \to \frac {df}{dx}=1\quad\frac {df}{dy}=1$

这就是说，无论其值如何， $x,y$ 的导数均为1。这是有道理的，因为无论增加 $x,y$ 中任一个的值，函数 $f$ 的值都会增加，并且增加的变化率独立于 $x,y$ 的具体值（情况和乘法操作不同）。取最大值操作也是常常使用的：
$\displaystyle f(x,y)=max(x,y) \to \frac {df}{dx}=1 (x>=y) \quad\frac {df}{dy}=1 (y>=x)$

上式是说，如果该变量比另一个变量大，那么梯度是1，反之为0。例如，若 $x=4,y=2$ ，那么max是4，所以函数对于 $y$ 就不敏感。也就是说，在 $y$ 上增加 $h$ ，函数还是输出为4，所以梯度是0：因为对于函数输出是没有效果的。当然，如果给 $y$ 增加一个很大的量，比如大于2，那么函数 $f$ 的值就变化了，但是导数并没有指明输入量有巨大变化情况对于函数的效果，他们只适用于输入量变化极小时的情况，因为定义已经指明： $lim_{h\to 0}$ 。

使用链式法则计算复合表达式

现在考虑更复杂的包含多个函数的复合函数，比如 $f(x,y,z)=(x+y)z$ 。虽然这个表达足够简单，可以直接微分，但是在此使用一种有助于读者直观理解反向传播的方法。将公式分成两部分： $q=x+y$ 和 $f=qz$ 。在前面已经介绍过如何对这分开的两个公式进行计算，因为 $f$ 是 $q$ 和 $z$ 相乘，所以 $\displaystyle\frac{\partial f}{\partial q}=z,\frac{\partial f}{\partial z}=q$ ，又因为 $q$ 是 $x$ 加 $y$ ，所以 $\displaystyle\frac{\partial q}{\partial x}=1,\frac{\partial q}{\partial y}=1$ 。然而，并不需要关心中间量 $q$ 的梯度，因为 $\frac{\partial f}{\partial q}$ 没有用。相反，函数 $f$ 关于 $x,y,z$ 的梯度才是需要关注的。链式法则指出将这些梯度表达式链接起来的正确方式是相乘，比如 $\displaystyle\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial x}$ 。在实际操作中，这只是简单地将两个梯度数值相乘，示例代码如下：

# 设置输入值
x = -2; y = 5; z = -4

# 进行前向传播
q = x + y # q becomes 3
f = q * z # f becomes -12

# 进行反向传播:
# 首先回传到 f = q * z
dfdz = q # df/dz = q, 所以关于z的梯度是3
dfdq = z # df/dq = z, 所以关于q的梯度是-4
# 现在回传到q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1. 这里的乘法是因为链式法则
dfdy = 1.0 * dfdq # dq/dy = 1

最后得到变量的梯度[dfdx, dfdy, dfdz]，它们告诉我们函数f对于变量[x, y, z]的敏感程度。这是一个最简单的反向传播。一般会使用一个更简洁的表达符号，这样就不用写df了。这就是说，用dq来代替dfdq，且总是假设梯度是关于最终输出的。

这次计算可以被可视化为如下计算线路图像：

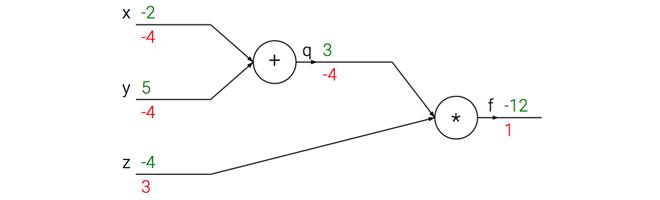
上图的真实值计算线路展示了计算的视觉化过程。前向传播从输入计算到输出（绿色），反向传播从尾部开始，根据链式法则递归地向前计算梯度（显示为红色），一直到网络的输入端。可以认为，梯度是从计算链路中回流。

简单理解

如下的神经网络

前向传播

对于节点 $h_1$ 来说， $h_1$ 的净输入 $net_{h_1}$ 如下：
$net_{h_1}=w_1\times i_1+w_2\times i_2+b_1\times 1$
接着对 $net_{h_1}$ 做一个sigmoid函数得到节点 $h_1$ 的输出：
$out_{h_1}=\frac{1}{1+e^{-net_{h_1}}}$
类似的，我们能得到节点 $h_2$ 、 $o_1$ 、 $o_2$ 的输出 $out_{h_2}$ 、 $out_{o_1}$ 、 $out_{o_2}$ 。

误差

得到结果后，整个神经网络的输出误差可以表示为：
$E_{total}=\sum\frac{1}{2}(target-output)^2$
其中 $output$ 就是刚刚通过前向传播算出来的 $out_{o_1}$ 、 $out_{o_2}$ ； $target$ 是节点 $o_1$ 、 $o_2$ 的目标值。 $E_{total}$ 用来衡量二者的误差。
这个 $E_{total}$ 也可以认为是cost function，不过这里省略了防止overfit的regularization term（ $\sum{w_i^2}$ ）
展开得到
$E_{total}=E{o_1}+E{o_2}=\frac{1}{2}(target_{o_1}-out_{o_1})^2+\frac{1}{2}(target_{o_2}-out_{o_2})^2$

后向传播

对输出层的 $w_5$

通过梯度下降调整 $w_5$ ，需要求 $\frac{\partial {E_{total}}}{\partial {w_5}}$ ，由链式法则：
$\frac{\partial {E_{total}}}{\partial {w_5}}=\frac{\partial {E_{total}}}{\partial {out_{o_1}}}\frac{\partial {out_{o_1}}}{\partial {net_{o_1}}}\frac{\partial {net_{o_1}}}{\partial {w_5}}$ ，
如下图所示：

$\frac{\partial {E_{total}}}{\partial {out_{o_1}}}=\frac{\partial}{\partial {out_{o_1}}}(\frac{1}{2}(target_{o_1}-out_{o_1})^2+\frac{1}{2}(target_{o_2}-out_{o_2})^2)=-(target_{o_1}-out_{o_1})$
$\frac{\partial {out_{o_1}}}{\partial {net_{o_1}}}=\frac{\partial }{\partial {net_{o_1}}}\frac{1}{1+e^{-net_{o_1}}}=out_{o_1}(1-out_{o_1})$
$\frac{\partial {net_{o_1}}}{\partial {w_5}}=\frac{\partial}{\partial {w_5}}(w_5\times out_{h_1}+w_6\times out_{h_2}+b_2\times 1)=out_{h_1}$
以上3个相乘得到梯度 $\frac{\partial {E_{total}}}{\partial {w_5}}$ ，之后就可以用这个梯度训练了：
$w_5^+=w_5-\eta \frac{\partial {E_{total}}}{\partial {w_5}}$

很多教材比如Stanford的课程，会把中间结果 $\frac{\partial {E_{total}}}{\partial {net_{o_1}}}=\frac{\partial {E_{total}}}{\partial {out_{o_1}}}\frac{\partial {out_{o_1}}}{\partial {net_{o_1}}}$ 记做 $\delta_{o_1}$ ，表示这个节点对最终的误差需要负多少责任。所以有 $\frac{\partial {E_{total}}}{\partial {w_5}}=\delta_{o_1}out_{h_1}$ 。

对隐藏层的 $w_1$

通过梯度下降调整 $w_1$ ，需要求 $\frac{\partial {E_{total}}}{\partial {w_1}}$ ，由链式法则：
$\frac{\partial {E_{total}}}{\partial {w_1}}=\frac{\partial {E_{total}}}{\partial {out_{h_1}}}\frac{\partial {out_{h_1}}}{\partial {net_{h_1}}}\frac{\partial {net_{h_1}}}{\partial {w_1}}$ ，

如下图所示：

参数 $w_1$ 影响了 $net_{h_1}$ ，进而影响了 $out_{h_1}$ ，之后又影响到 $E_{o_1}$ 、 $E_{o_2}$ 。
求解每个部分：
$\frac{\partial {E_{total}}}{\partial {out_{h_1}}}=\frac{\partial {E_{o_1}}}{\partial {out_{h_1}}}+\frac{\partial {E_{o_2}}}{\partial {out_{h_1}}}$ ，
其中 $\frac{\partial {E_{o_1}}}{\partial {out_{h_1}}}=\frac{\partial {E_{o_1}}}{\partial {net_{o_1}}}\times \frac{\partial {net_{o_1}}}{\partial {out_{h_1}}}=\delta_{o_1}\times \frac{\partial {net_{o_1}}}{\partial {out_{h_1}}}=\delta_{o_1}\times \frac{\partial}{\partial {out_{h_1}}}(w_5\times out_{h_1}+w_6\times out_{h_2}+b_2\times 1)=\delta_{o_1}w_5$ ，这里 $\delta_{o_1}$ 之前计算过。
$\frac{\partial {E_{o_2}}}{\partial {out_{h_1}}}$ 的计算也类似，所以得到
$\frac{\partial {E_{total}}}{\partial {out_{h_1}}}=\delta_{o_1}w_5+\delta_{o_2}w_7$ 。
$\frac{\partial {E_{total}}}{\partial {w_1}}$ 的链式中其他两项如下：
$\frac{\partial {out_{h_1}}}{\partial {net_{h_1}}}=out_{h_1}(1-out_{h_1})$ ，
$\frac{\partial {net_{h_1}}}{\partial {w_1}}=\frac{\partial }{\partial {w_1}}(w_1\times i_1+w_2\times i_2+b_1\times 1)=i_1$
相乘得到
$\frac{\partial {E_{total}}}{\partial {w_1}}=\frac{\partial {E_{total}}}{\partial {out_{h_1}}}\frac{\partial {out_{h_1}}}{\partial {net_{h_1}}}\frac{\partial {net_{h_1}}}{\partial {w_1}}=(\delta_{o_1}w_5+\delta_{o_2}w_7)\times out_{h_1}(1-out_{h_1}) \times i_1$
得到梯度后，就可以对 $w_1$ 迭代了：
$w_1^+=w_1-\eta \frac{\partial{E_{total}}}{\partial{w_1}}$ 。

在前一个式子里同样可以对 $\delta_{h_1}$ 进行定义， $\delta_{h_1}=\frac{\partial {E_{total}}}{\partial {out_{h_1}}}\frac{\partial {out_{h_1}}}{\partial {net_{h_1}}}=(\delta_{o_1}w_5+\delta_{o_2}w_7)\times out_{h_1}(1-out_{h_1}) =(\sum_o \delta_ow_{ho})\times out_{h_1}(1-out_{h_1})$ ，所以整个梯度可以写成 $\frac{\partial {E_{total}}}{\partial {w_1}}=\delta_{h_1}\times i_1$