关于奈奎斯特稳定判据应用中的理解

根据上一篇文章，我们知道要想判定系统稳定性，只需要找到当 $S$绕奈奎斯特路径一圈后， $G(s)H(s)$所经过的路径绕 $(-1, j0)$的次数就可以了，现在我们就来深入探讨当 $S$绕奈奎斯特路径一圈后， $G(s)H(s)$的路径到底是什么样，

接下来我们分为两种情况讨论

1. $G(s)H(s)$在虚轴上无极点

图1

函数在虚轴上时的情况很简单，我们不予讨论，我们主要讨论一下，函数在大圆弧上的情况。
设 $S = \lim\limits_{R\to\infty}Re^{-j\phi}$它在GH平面上的映射为
$G(s)H(s) \mid_{s = \lim\limits_{R\to\infty}Re^{-j\phi}} = \Bigl(\lim\limits_{R\to\infty}\frac{b_m}{a_n}\centerdot\frac{1}{R^{n - m}}\Bigr)e^{j(n - m)\phi}$

（推导过程自己弄）
当n = m 时
$G(s)H(s) \mid_{s = \lim\limits_{R\to\infty}Re^{-j\phi}} = \frac{b_m}{a_n} = K$
即圆弧映射为常数K
当 $n>m时$，
$G(s)H(s) \mid_{s = \lim\limits_{R\to\infty}Re^{-j\phi}} = 0$
即圆弧映射为原点

2. $G(s)H(s)$在虚轴上有极点

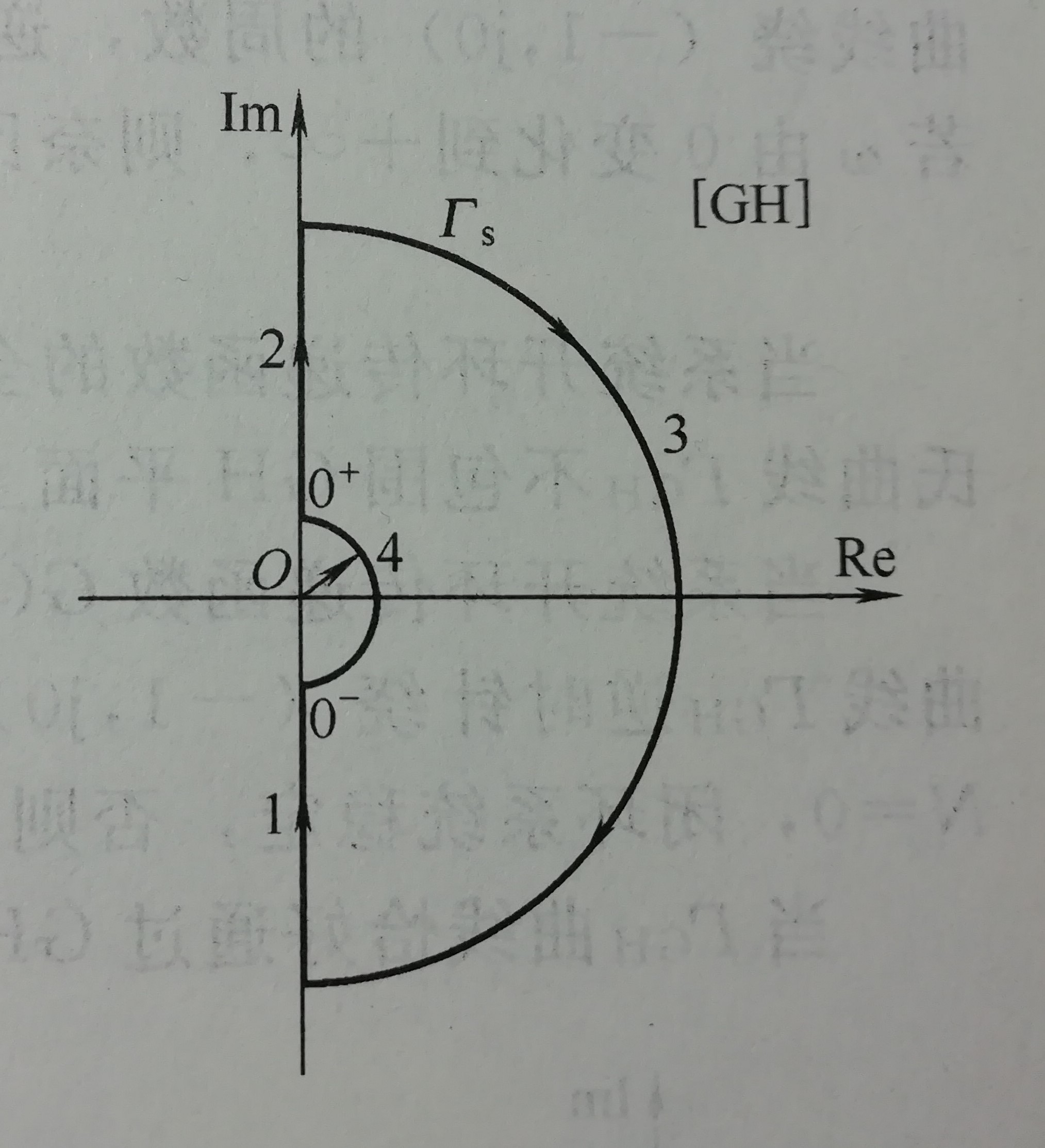图2

我们现在只关注那个小圆弧即 $s = \lim\limits_{R\to0}Re^{j\theta}(-\frac{\pi}{2}\leqslant-\frac{\pi}{2})$，
设系统开环传递函数为
$G(s)H(s) = \frac{k(s-z_1)(s-z_2)\mathellipsis(s-z_m)}{s^{\nu}(s-p_1)(s-p_2)\mathellipsis(s-p_m)}$
$\nu$称为系统型别，经过推导可以得到
$G(s)H(s)\mid_{s=\lim\limits_{r\to0}re^{j\theta}}=\lim\limits_{r\to0}\frac{K}{r^{\nu}}e^{-j\nu\theta}$

上式表明，当 $s$在小圆弧上逆时针变化时 $G(s)H(s)$的变化轨迹是一个顺时针的无穷大的圆弧，弧度为 $\nu\pi$