摘要:该系列为DR_CAN Advanced控制理论视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
1 一个反馈控制系统
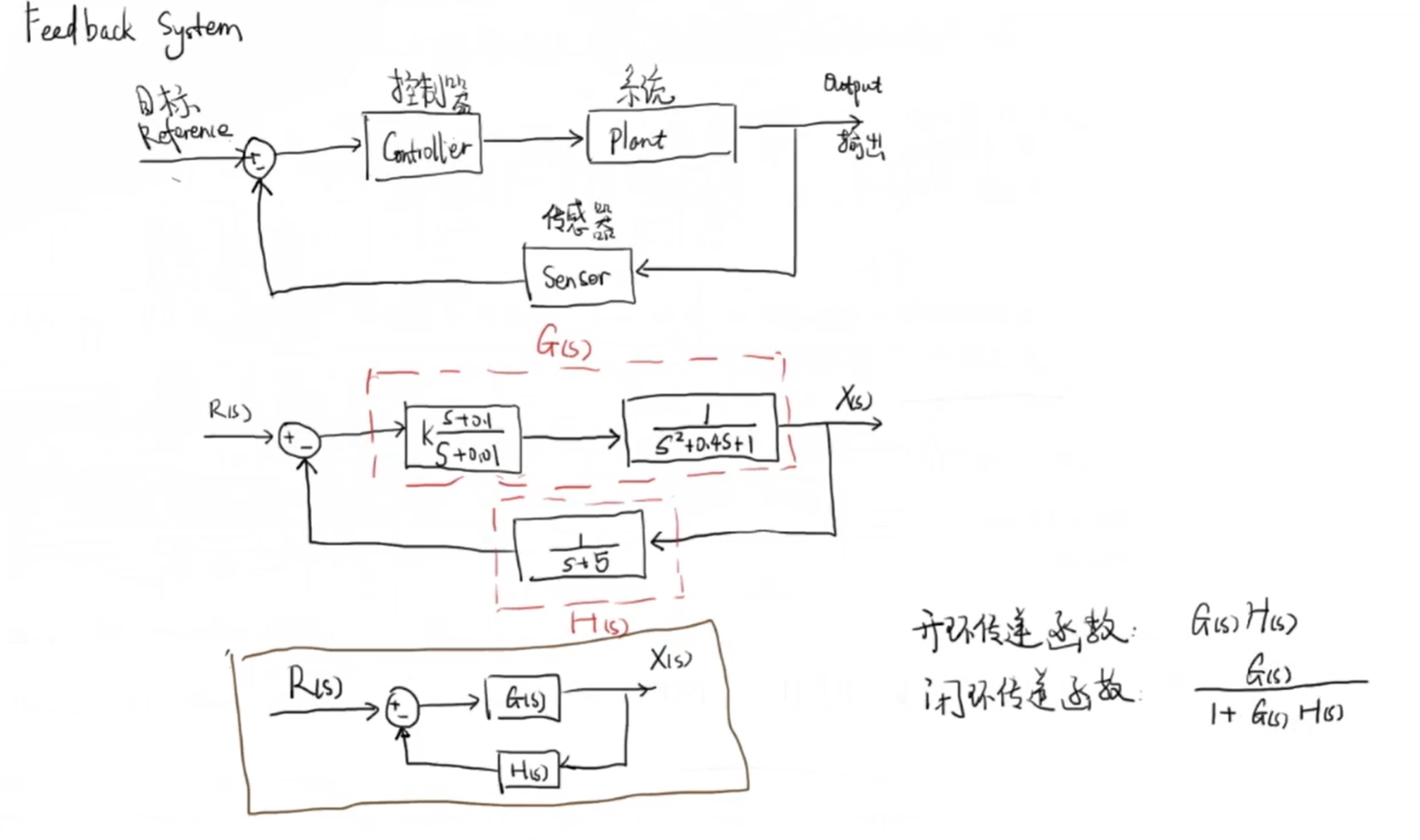
将函数写为分子分母的形式可得到以下结论:
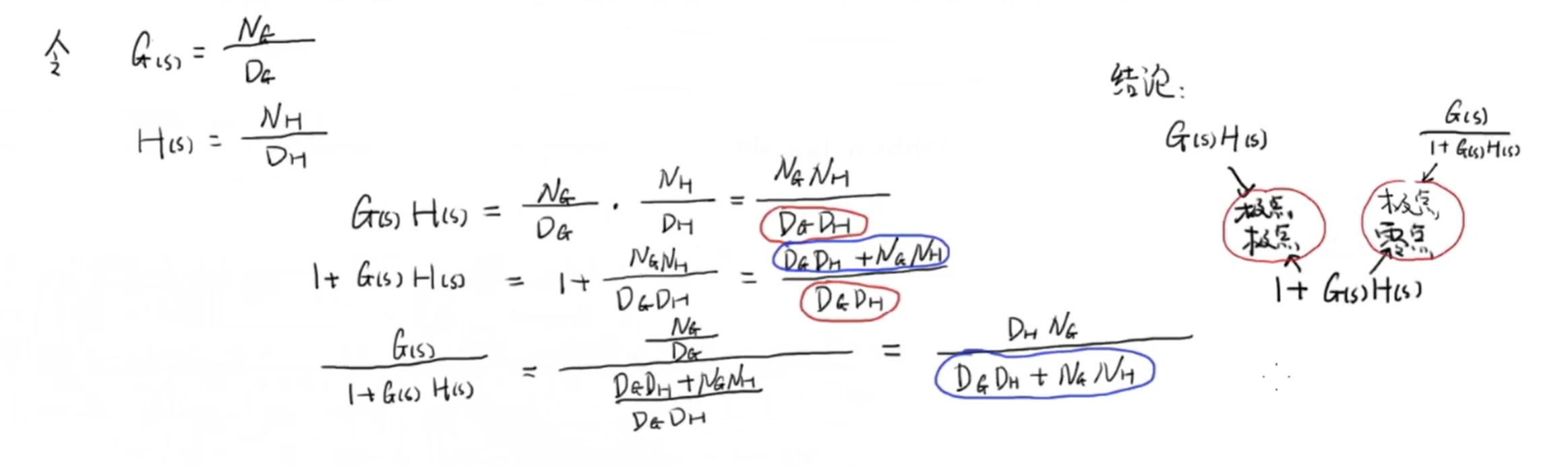
以上结论很重要,因为这个结论通过 \(1+G(s)H(s)\) 将开环传递函数与闭环传递函数联系在一起。
2 柯西幅角原理
函数存在一个零点:
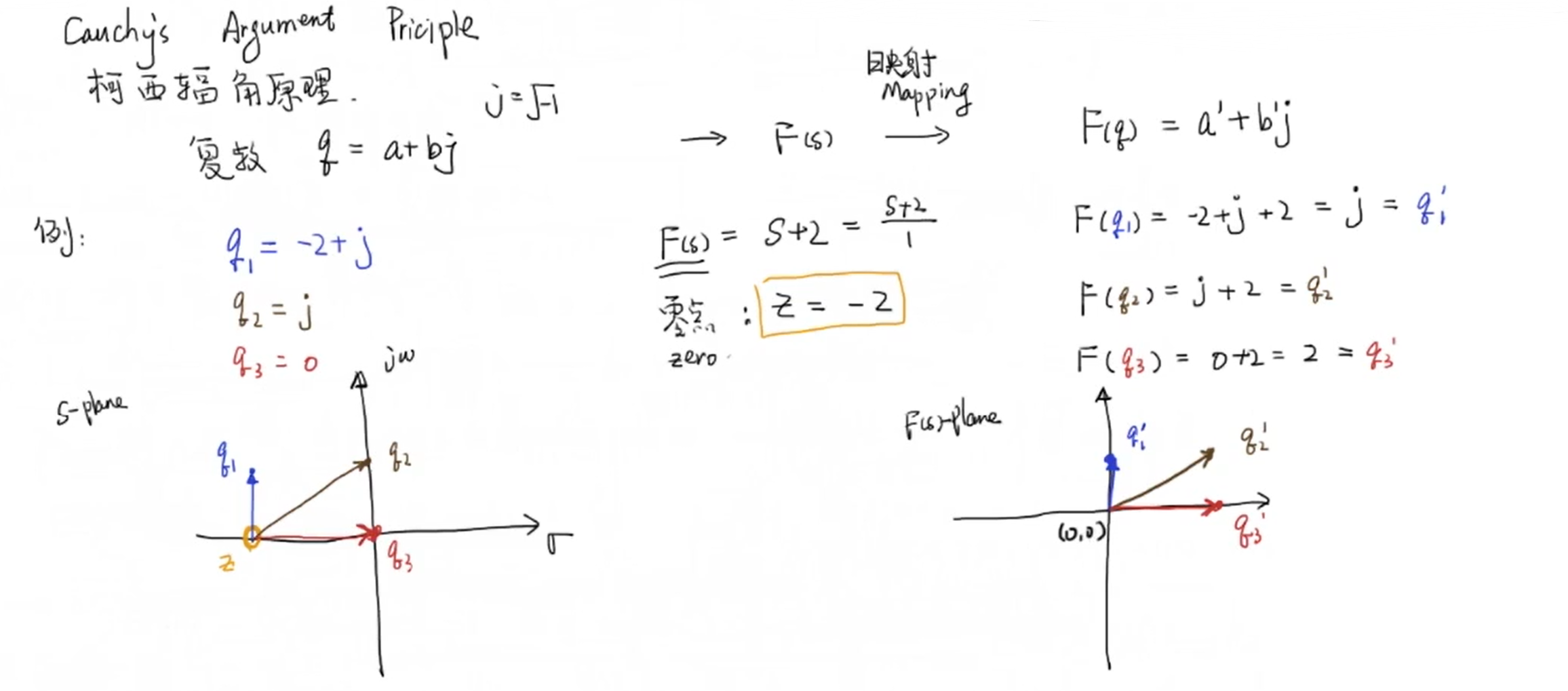
函数存在一个极点:
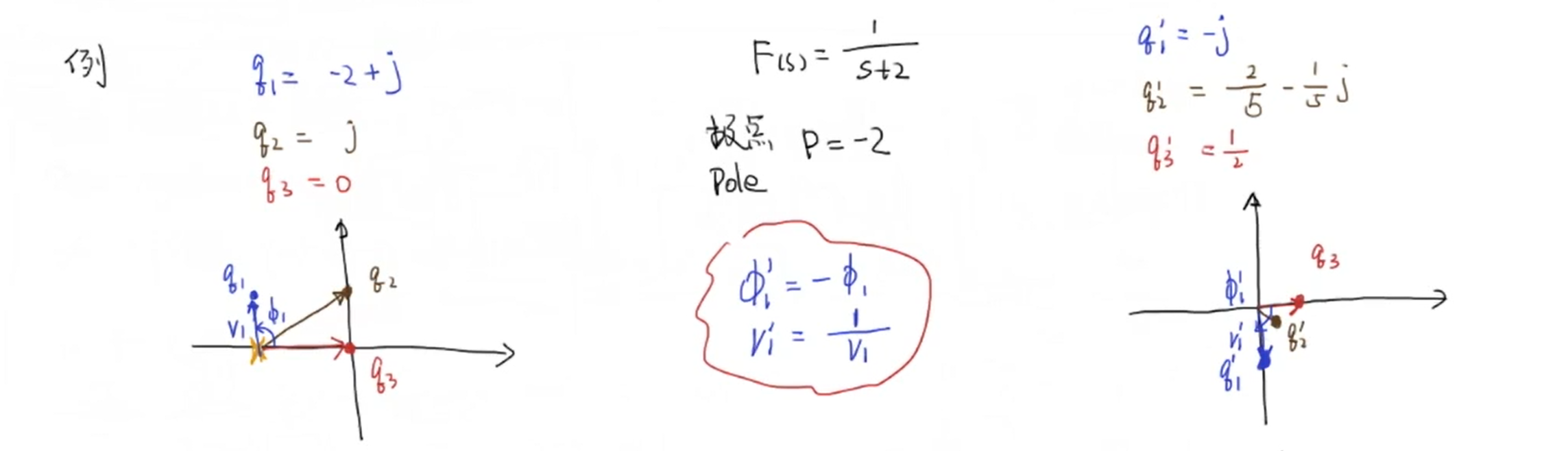
函数存在一个零点和一个极点:
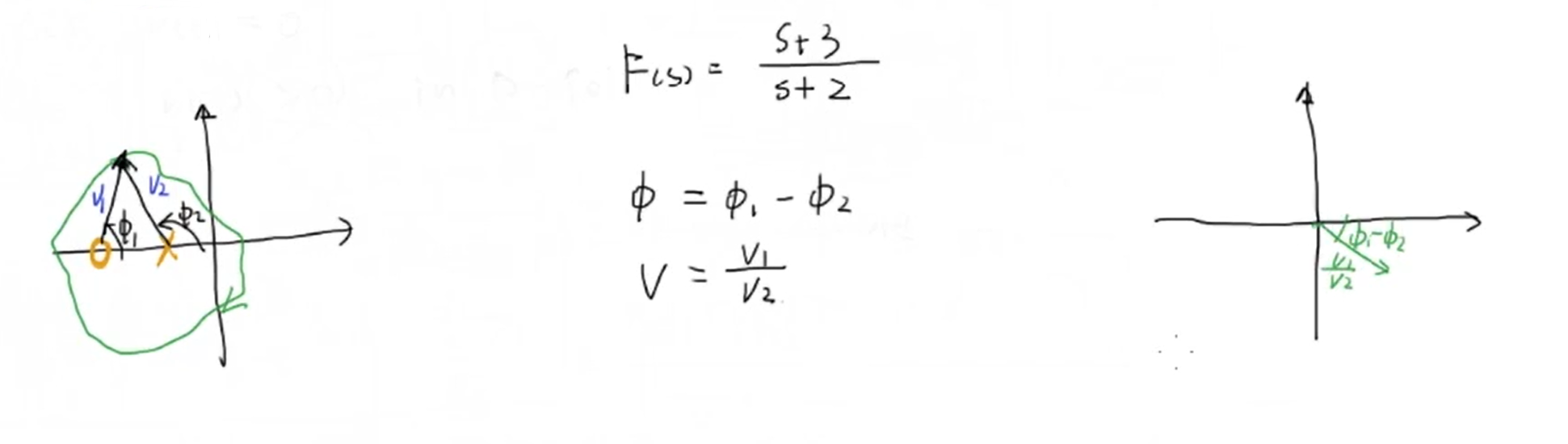
结论: \(S\) 平面内存在一条顺时针曲线 \(A\),\(B\) 曲线曲线 \(A\) 是通过函数 \(F(s)\) 的映射。\(A\) 曲线每包含一个 \(F(s)\) 的零点,\(B\) 曲线就绕原点顺时针一圈。\(A\) 曲线每包含一个 \(F(s)\) 的极点,\(B\) 曲线就绕原点逆时针一圈。
一个例子,如果映射后的曲线绕原点逆时针两圈,则原曲线所包含的极点数比零点数多2。

3 奈奎斯特稳定性判据
奈奎斯特曲线是包含整个 \(S\) 平面右半部分的曲线,我们另 \(F(s) = 1+G(s)H(s)\) ,有 \(P - Z = N\), 其中 \(N\) 为 映射后 \(B\) 曲线绕原点的逆时针圈数:

根据 1 中推导出的零点极点关系,我们可以将 \(P - Z = N\) 写成以下形式:

接下来,我们令 \(F(s) = G(s)H(s)\) ,也就是让刚才的 \(F(s)-1\) ,由于函数是线性的,因此这使得映射后 \(B\) 曲线在 \(S\) 平面中向左移动了一个实数单位,而 \(P - Z = N\) 中的 \(N\) 从绕原点的逆时针圈数变成了绕 \((-1,0)\) 的逆时针圈数。而这个新的曲线就是奈奎斯特图(Nyquist Plot)。
总结一下,如果系统稳定,则闭环传递函数在复平面右侧无极点,及 \(Z=0\) ,因此绕 \((-1,0)\) 的逆时针圈数即为开环传递函数的极点个数,这就是奈奎斯特稳定性判据。

4 回到开头的例子
经过计算我们发现开环传递函数的极点均位于复平面左侧:
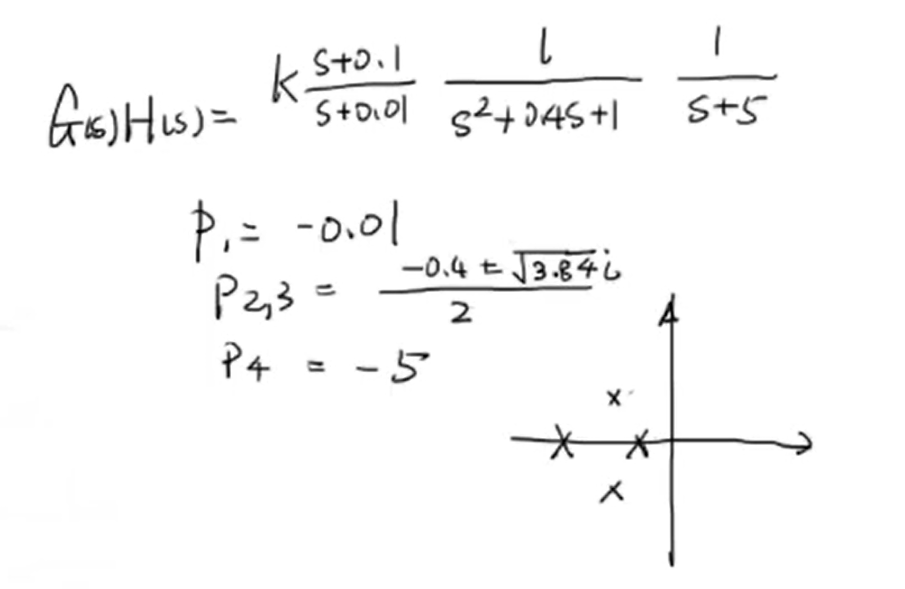
通过MATLAB可以画出这个闭环系统的奈奎斯特图:
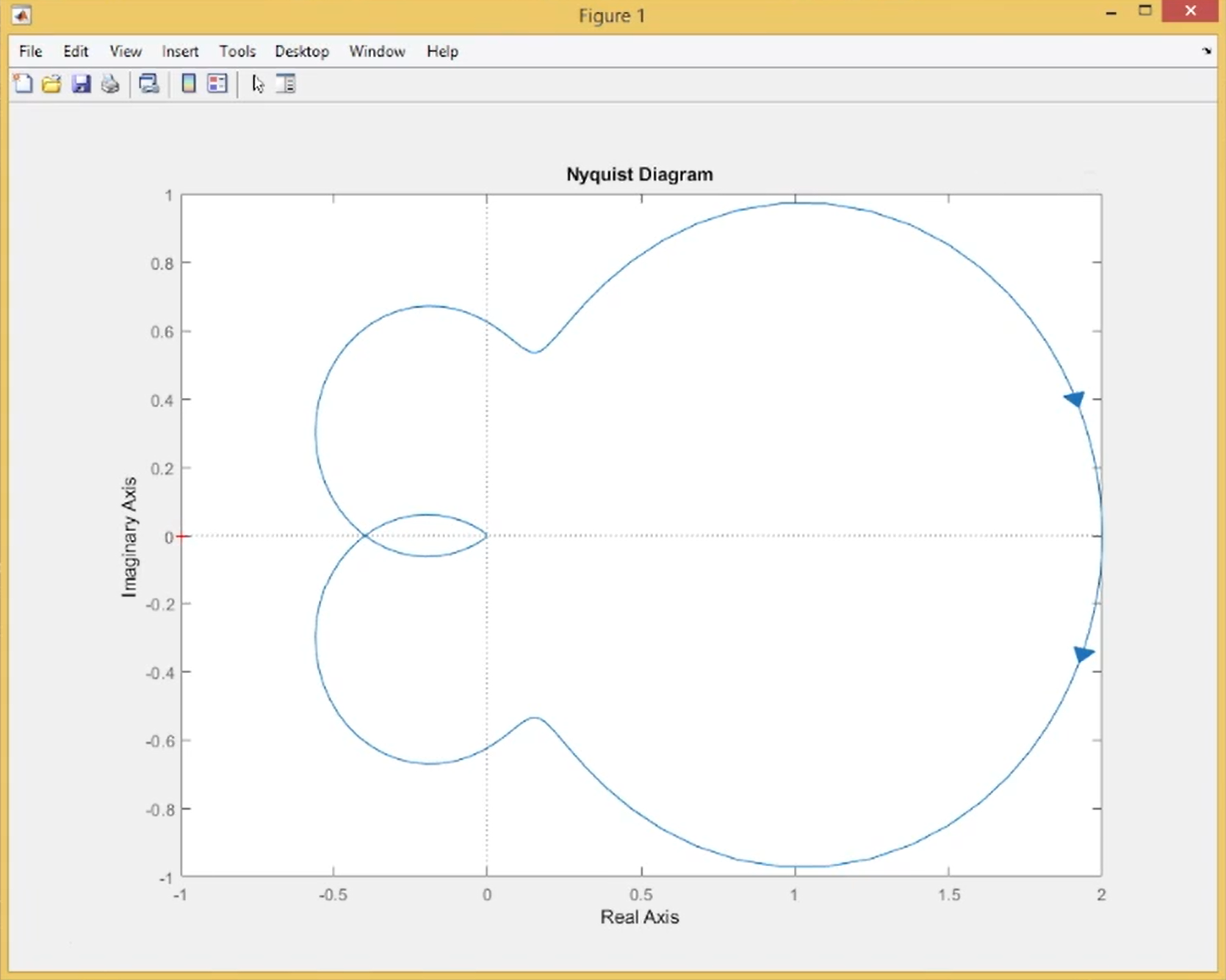
我们发现曲线并没有包含 \((-1,0)\) ,也就是说在 \(P - Z = N\) 中 \(N=0\),又因为 \(P=0\) 因此 \(Z = 0\) ,也就是说系统的闭环传递函数在复平面右侧没有极点,因此系统是稳定的。
接下来我们增大控制器的增益 \(k\) ,由于映射是线性的,因此图像结果是等比放大:
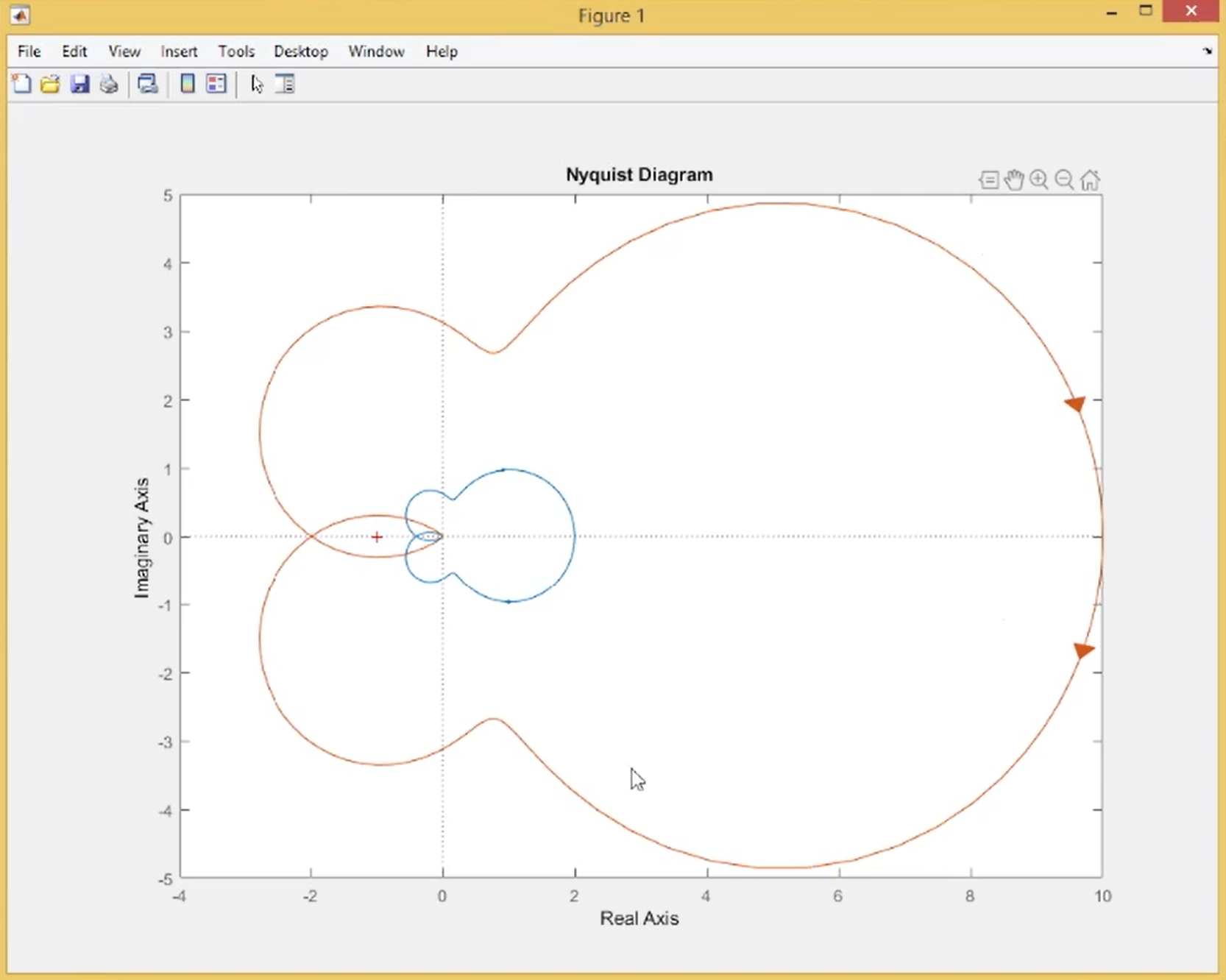
我们发现这时曲线包含 \((-1,0)\) 并且绕其顺时针旋转了两圈,也就意味着 \(P - Z = N\) 中 \(N=\),-2又因为 \(P=0\) 因此 \(Z = 2\) ,也就是说系统的闭环传递函数在复平面右侧有两个极点,因此系统是不稳定的。