题意:
本质不同的集合:不存在两个方案重新编号之后对应的边集相同(对于所有x,y,,(x,y)边颜色都相同)。
(1≤ N≤ 53, 1≤ M≤ 1000)
对P取模
本质不同,想到置换
置换在哪里?
就是重新编号
本质是一个n!大小的置换群
不能枚举每一个置换了,考虑对相同的置换一起处理
置换之后也要找环,所以直接枚举环的情况,处理对应这种环的组合的置换的出现次数,再处理环的组合的不动点
自然数拆分出环
环长为li,有k个,对应置换个数:
如果每一个都不同:$\frac{n!}{(l1!*l2!..lk!)}*((l1-1)!)*((l2-1)!)*((lk-1)!)$
如果
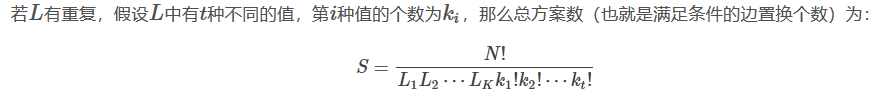
就是分配环的所属的时候,大小相同的环都是相同的。
所以再进行一次多重集合的排列。
每个置换的不动点个数:
考虑环自己内部连边的“环”个数:$1+\lfloor \frac{l-2}{2} \rfloor$
证明考虑边上相隔1一定一种,相隔若干会连出一些,手画几个
2->1
3->1
4->2
5->2
6->3
7->3
环与环之间的连边的“环”个数:$gcd(l1,l2)$
一个连边的颜色,会走$lcm(l1,l2)$才会重复,
期间l1的每个点连出去了lcm(l1,l2)/l1=l2/gcd(l1,l2)
一共连出去l2个点,每确定一个颜色就确定了l2/gcd(l1,l2)个颜色,所以共有gcd(l1,l2)个“环”
环总数tot
每个环m种颜色,m^tot即可。
1.自然数拆分+计算对应置换个数->枚举所有置换
2.每个自然数拆分计算不动点个数+再乘上对应置换个数->处理所有不动点
完毕。