【ML学习笔记】25：PCA及绘制降维与恢复示意图

主成分分析

简述

主成分分析意在学习一个映射 $U_{reduce}$ ，能将高维数据投射到低维空间上（在矩阵表示中即将数据的列变少），PCA后的低维空间数据可通过映射 $U_{reduce}^T$ 还原成高维数据的近似。PCA意在使得在指定维度的低维表示中，投射误差总是最小。在ML中即用于将 $m$ 个样本的特征数目从 $n$ 减少到 $k$ 。

归一化

设样本的特征矩阵 $A$ 是 $m$ 行 $n$ 列的，第 $i$ 行第 $j$ 列的 $a_j^{(i)}$ 即是第 $i$ 个样本的第 $j$ 个特征的值。数据归一化是使样本的特征的均值为0，第 $j$ 个特征在 $m$ 个样本的样本集中的均值
$\mu_j=\frac{1}{m} \sum_{i=1}^m a_j^{(i)}$
数据归一化即是使
$x_j^{(i)}=a_j^{(i)}-\mu_j$

缩放

不同的特征值很可能取值范围相差很大，缩放即使特征的最大最小值之差恰为1。取每个特征的最大最小值之差
$s_j=max(a_j^{(i)})-min(a_j^{(i)}) \equiv max(x_j^{(i)})-min(x_j^{(i)})$
对归一化后的数据进行缩放，即
$x_j^{(i)}=\frac{x_j^{(i)}}{s_j}=\frac{a_j^{(i)}-\mu_j}{s_j}$

PCA降维

前面的归一化和缩放属于数据预处理的过程，得到的还是 $m\times n$ 的矩阵 $X$ ，先计算样本协方差矩阵 $\Sigma$
$\Sigma=\frac{1}{m}X^TX$
对其做SVD，得到
$[U,S,V]=svd(\Sigma)$
因为前面得到的 $\Sigma$ 是 $n\times n$ 的，行数为 $n$ ，所以 $U$ 是 $n$ 阶方阵，其列空间由左奇异向量组成
$U=[\pmb{u}_1,\pmb{u}_2,...,\pmb{u}_n]$
样本协方差矩阵 $\Sigma$ 可以由这些特征向量线性表出。在约定奇异值在主对角线上从大到小排列的要求下，只要选取前 $k$ 个列向量，组成主成分特征矩阵
$U_{reduce}=[\pmb{u}_1,\pmb{u}_2,...,\pmb{u}_k]$
其维度是 $n\times k$ ，则可以用其对样本矩阵 $X$ 的特征做降维
$Z=XU_{reduce}$
其中， $Z$ 的行向量 $\pmb{z}^{(i)}$ 就是第 $i$ 个样本的特征向量 $\pmb{x}^{(i)}$ 在主成分特征矩阵 $U_{reduce}$ 表示的线性空间上的投影
$\pmb{z}^{(i)}=U_{reduce}^T \pmb{x}^{(i)}$

PCA恢复

由上式，对 $\pmb {x}^{(i)}$ 的近似
$\pmb{x}_{approx}^{(i)}=U_{reduce} \pmb{z}^{(i)}$
所以
$X_{approx}=ZU_{reduce}^T$

numpy实现PCA

主要是numpy就已经实现了SVD，所以可以很方便的实现PCA。

数据预处理和降维

import numpy as np
from matplotlib import pyplot as plt
import matplotlib

matplotlib.rcParams['axes.unicode_minus'] = False

# 原始矩阵
A = np.array([
    [3, 2000],
    [2, 3000],
    [4, 5000],
    [5, 8000],
    [1, 2000]
])
# m行n列
m, n = A.shape

# 数据归一化:先计算每一列(特征)的均值,再用自动广播让每行(样本)减去均值
mean = np.mean(A, axis=0)
norm = A - mean

# 数据缩放:先计算每一列的最大最小值之差,再用自动广播让每一行除以这个差
scope = np.max(norm, axis=0) - np.min(norm, axis=0)
X = norm / scope

# 计算协方差矩阵Sigma(n阶方阵)
Sigma = (1.0 / m) * np.dot(X.T, X)

# 对协方差矩阵做奇异值分解
U, S, V = np.linalg.svd(Sigma)

# 因为是将二维(列)的数据变成一维(列),所以k=1
k = 1

# 取特征矩阵U(n阶方阵)的前k列构造主成分特征矩阵U_reduce(n行k列)
U_reduce = U[:, 0:k].reshape(n, k)

# 对数据进行降维,降维后的Z(m行k列)=X(m行n列)乘以U_reduce(n行k列)
Z = np.dot(X, U_reduce)
print(Z)

[[ 0.2452941 ]
[ 0.29192442]
[-0.29192442]
[-0.82914294]
[ 0.58384884]]

数据恢复

# 还原得到近似数据
X_approx = np.dot(Z, U_reduce.T)
A_approx = X_approx * scope + mean  # 这里书上用np.multiply也可以
print(A_approx)

[[2.33563616e+00 2.91695452e+03]
[2.20934082e+00 2.71106794e+03]
[3.79065918e+00 5.28893206e+03]
[5.24568220e+00 7.66090960e+03]
[1.41868164e+00 1.42213588e+03]]

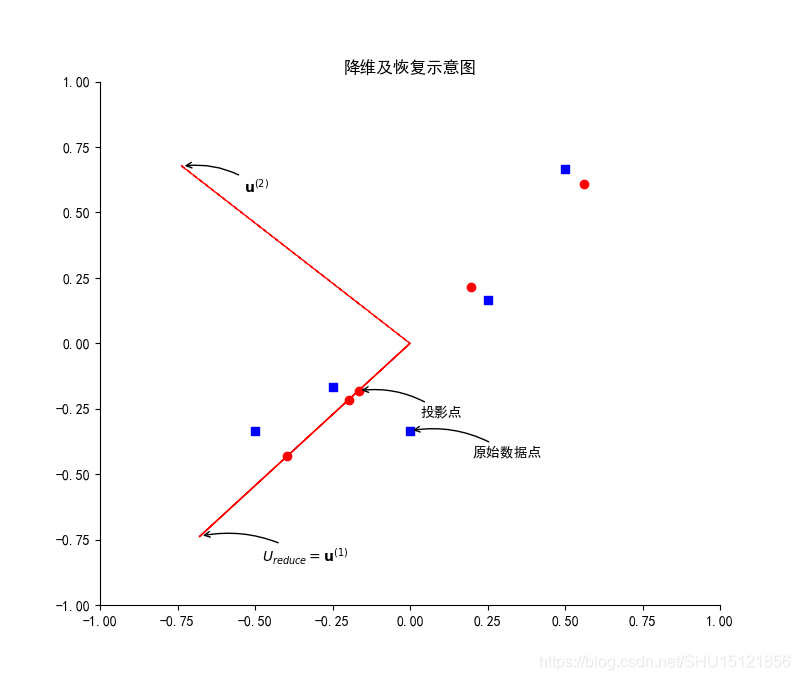
绘制降维及恢复示意图

# 绘图面板
plt.figure(figsize=(8, 8), dpi=100)
plt.title("降维及恢复示意图")
# 坐标最小最大值
mm = (-1, 1)
plt.xlim(*mm)
plt.ylim(*mm)
# 右/上坐标轴透明
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
# 绘制归一化之后的数据点
plt.scatter(X[:, 0], X[:, 1], marker='s', c='b')
# 绘制还原回来的数据点
plt.scatter(X_approx[:, 0], X_approx[:, 1], marker='o', c='r')
# 绘制主成分特征向量,即主成分特征矩阵U的n个列向量
plt.arrow(0, 0, U[0, 0], U[1, 0], color='r', linestyle='-')
plt.arrow(0, 0, U[0, 1], U[1, 1], color='r', linestyle='--')
# 接下来要在图上绘制标注,下面是提取出来的要给plt.annotate()用的一些参数
tit = [  # 标题
    r"$U_{reduce}=\mathbf{u}^{(1)}$",
    r"$\mathbf{u}^{(2)}$",
    "原始数据点",
    "投影点"
]
xy = [  # xy指定剪头尖端位置
    (U[0, 0], U[1, 0]),
    (U[0, 1], U[1, 1]),
    (X[0, 0], X[0, 1]),
    (X_approx[0, 0], X_approx[0, 1])
]
# xytest指定标注文本位置,用这个函数来从xy生成
pian = lambda a, b: (a + 0.2, b - 0.1)
# xycoords='data'表示使用轴坐标系,arrowprops指定箭头的属性.在这个嵌套dict中可以看到两种定义字典的写法
kw = {'xycoords': 'data', 'fontsize': 10, 'arrowprops': dict(arrowstyle="->", connectionstyle="arc3,rad=.2")}
# 绘制四个标注
for i in range(len(tit)):
    plt.annotate(tit[i], xy=xy[i], xytext=pian(*xy[i]), **kw)
plt.show()

在这里插入图片描述