斐波那契数列的三种实现方式（递归、循环、矩阵）

《剑指offer》里讲到了一种斐波那契数列的 O(logN) 时间复杂度的实现，觉得挺有意思的，三种方法都记录一下。

一、递归

一般来说递归实现的代码都要比循环要简洁，但是效率不高，比如递归计算斐波那契数列第n个元素。

long long Fibonacci_Solution1(unsigned int n)
{
    // printf("%d ", n);
    if (n <= 0) return 0;
    if (n == 1) return 1;
    return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2);
}

如果计算数列的第4个位置上（从0开始）的数（0 1 1 2 3），也就是3，上边的 printf 输出应该是 4 3 2 1 0 1 2 1 0，这是因为计算 F(4) 要计算 F(3) 和 F(2)，而计算 F(3) 的时候又要计算 F(2) 和 F(1)，所以会有很多重复计算。用下图可以更好地说明。

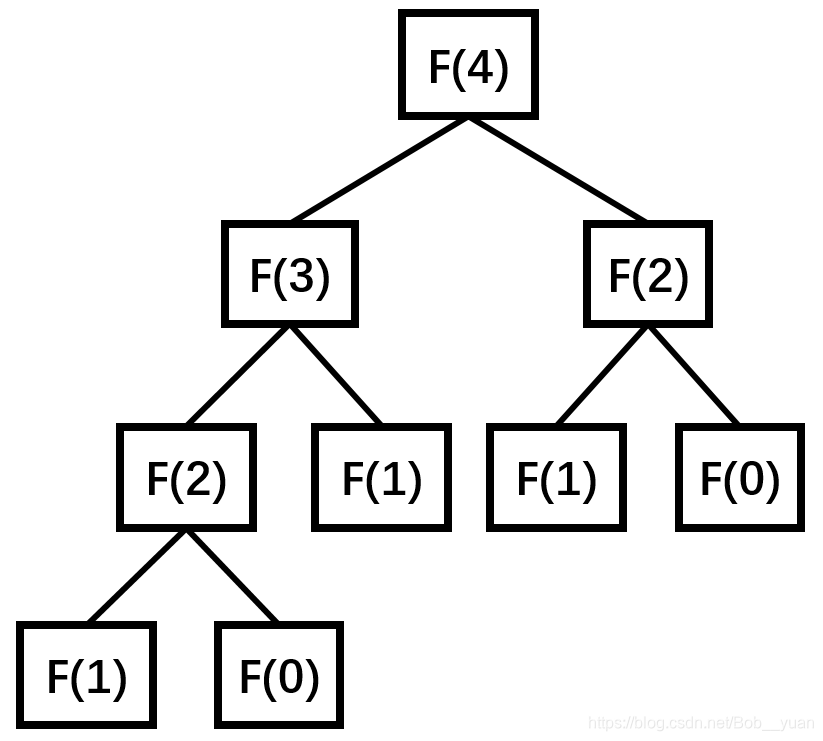
递归虽然有简洁的优点，但它同时也有显著地缺点。递归由于是函数调用自身，而函数调用是有空间和时间的消耗的：每一次函数调用，都需要在内存栈中分配空间以保存参数、返回地址及临时变量，而且往栈里压入数据和弹出数据都需要时间。

而且除了效率问题之外，递归可能引起 调用栈溢出，因为需要为每一次函数调用在内存栈中分配空间，而每个进程的栈的容量是有限的。当蒂固的层级太多，就会超出栈的容量，导致栈溢出。比如上边的代码，输入40，可以正确返回 12502500，但是输入 5000 就会出错。

二、循环

最常规的正确做法就是用循环从小到大计算。

long long Fibonacci_Solution2(unsigned n)
{
    if (n <= 0) return 0;
    if (n == 1) return 1;
    long long  fib1 = 1, fib0 = 0, fibN = 0;
    for (unsigned int i = 2; i <= n; ++i)
    {
        fibN = fib1 + fib0;
        fib0 = fib1;
        fib1 = fibN;
    }
    return fibN;
}

或者下边这种

long long Fibonacci_Solution2(unsigned n)
{
    if (n <= 0) return 0;
    if (n == 1) return 1;
    long long a = 0, b = 1;
    for (unsigned int i = 2; i <= n; ++i)
    {
        b = a + b;
        a = b - a;
    }
    return b;
}

三、矩阵

数中提到了一种 O(logN) 时间复杂度的算法，就是利用数学公式计算。

首先需要知道下边这个数学公式：

$\begin{bmatrix} f(n) &f(n - 1) \\f(n - 1) & f(n - 2) \end{bmatrix} = \begin{bmatrix} 1& 1\\ 1 & 0 \end{bmatrix}^{n - 1}$

这个公式用数学归纳法可以证明，所以只需要计算右边矩阵的 n-1 次方就能得到 f(n)，现在问题就变成了计算 2x2 矩阵的 n-1 次方，这样做 n-2 次乘法就可以了，时间复杂度还是 O(N)，但是还可以加速，如下式：

$a^{n} = \left\{\begin{matrix} a^{n/2}\cdot a^{n/2} &, n\; is\; even \\ a^{\left ( n-1 \right )/2}\cdot a^{\left ( n-1 \right )/2}\cdot a &, n\; is\; odd \end{matrix}\right.$

所以我们可以看出，想求 n 次方可以求出 n / 2 次方再平方，所以时间复杂度可以将为 O(logN)。

struct Matrix2By2
{
    Matrix2By2(long long m00 = 0, long long m01 = 0, long long m10 = 0,	long long m11 = 0)
        :m_00(m00), m_01(m01), m_10(m10), m_11(m11) {}
    long long m_00, m_01, m_10, m_11;
};

Matrix2By2 MatrixMultiply(const Matrix2By2& matrix1, const Matrix2By2& matrix2)
{
    return Matrix2By2(  matrix1.m_00 * matrix2.m_00 + matrix1.m_01 * matrix2.m_10,
                        matrix1.m_00 * matrix2.m_01 + matrix1.m_01 * matrix2.m_11,
                        matrix1.m_10 * matrix2.m_00 + matrix1.m_11 * matrix2.m_10,
                        matrix1.m_10 * matrix2.m_01 + matrix1.m_11 * matrix2.m_11    );
}

Matrix2By2 MatrixPower(unsigned int n)
{
    assert(n > 0);
    Matrix2By2 matrix;
    if (n == 1)
        matrix = Matrix2By2(1, 1, 1, 0);
    else if (n % 2 == 0)	// n是偶数
    {
        matrix = MatrixPower(n / 2);
        matrix = MatrixMultiply(matrix, matrix);
    }
    else if (n % 2 == 1)	// n是奇数
    {
        matrix = MatrixPower((n - 1) / 2);
        matrix = MatrixMultiply(matrix, matrix);
        matrix = MatrixMultiply(matrix, Matrix2By2(1, 1, 1, 0));
    }
    return matrix;
}

long long Fibonacci_Solution3(unsigned int n)
{
    if (n <= 0) return 0;
    if (n == 1) return 1;
    Matrix2By2 PowerNMinus2 = MatrixPower(n - 1);
    return PowerNMinus2.m_00;
}

为了测试上边三种方式的代码的正确性，可以用如下样例来测试。

// ====================测试代码====================
void Test(int n, int expected)
{
    if (Fibonacci_Solution1(n) == expected)
        printf("Test for %d in solution1 passed.\n", n);
    else
        printf("Test for %d in solution1 failed.\n", n);

    if (Fibonacci_Solution2(n) == expected)
        printf("Test for %d in solution2 passed.\n", n);
    else
        printf("Test for %d in solution2 failed.\n", n);

    if (Fibonacci_Solution3(n) == expected)
        printf("Test for %d in solution3 passed.\n", n);
    else
        printf("Test for %d in solution3 failed.\n", n);
}

int main(int argc, char* argv[])
{
    Test(0, 0);
    Test(1, 1);
    Test(2, 1);
    Test(3, 2);
    Test(4, 3);
    Test(5, 5);
    Test(6, 8);
    Test(7, 13);
    Test(8, 21);
    Test(9, 34);
    Test(10, 55);
    Test(40, 102334155);
    return 0;
}