版权声明:有女朋友的老江的博客,转载请告知老江 https://blog.csdn.net/qq_42367531/article/details/85009575
目录
【题目描述】
原题来自:SCOI 2010
在一个 2 维平面上有两条传送带,每一条传送带可以看成是一条线段。两条传送带分别为线段 AB 和线段 CD。lxhgww 在 AB 上的移动速度为 P ,在 CD 上的移动速度为 Q ,在平面上的移动速度 R。现在 lxhgww 想从 A 点走到 D 点,他想知道最少需要走多长时间。
【输入格式】
输入数据第一行是 4 个整数,表示 A 和 B 的坐标,分别为 Ax,Ay,Bx,By;
第二行是 4 个整数,表示 C 和 D 的坐标,分别为 Cx,Cy,Dx,Dy;
第三行是 3 个整数,分别是 P,Q,R。
【输出格式】
输出数据为一行,表示 lxhgww 从 A 点走到 D 点的最短时间,保留到小数点后 2 位。
【样例输入】
0 0 0 100
100 0 100 100
2 2 1【样例输出】
136.60【数据范围与提示】
对于 100% 的数据,1≤Ax,Ay,Bx,By,Cx,Cy,Dx,Dy≤1000,1≤P,Q,R≤10。
这道题一看到显然我是知道可以用三分的,但是发现有了三分之后就有点小难过,因为三分之后就没有了思路,所以感谢大佬的博客(建议先看完大佬的博客再来细节了解)。
这道题有好几个大思路,好几个小思路
一、三分(绝大多数人第一个想到的)
1、三分坐标直接求值
这是最常见的思路了,很多大佬都是用三分坐标的,因为很好理解。

我们进行三分套三分,把线段 三分寻找转折点后从转折点跑向线段
三分寻找转折点后从转折点跑向线段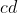 ,然后再在线段
,然后再在线段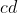 上三分寻找抵达地点跑向点
上三分寻找抵达地点跑向点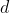 。(参考)【大佬代码】
。(参考)【大佬代码】
2.三分比值
这个是我重点要讲的,也是我觉得最方便最好解释的方法。
上网看了大佬的博客,发现可以三分比值。具体如下:
我们现在已知线段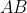 ,假设现在在
,假设现在在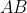 上已找到一点
上已找到一点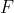 ,我们要去计算
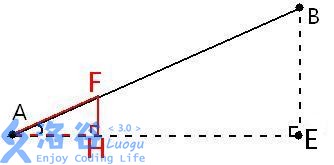
,我们要去计算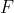 与另一条线段的距离,同时这个F点其实就是在AB上的一个转折点,这个
与另一条线段的距离,同时这个F点其实就是在AB上的一个转折点,这个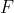 的坐标怎么求呢?
的坐标怎么求呢?
以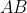 为斜边,作一个
为斜边,作一个 。作
。作 ,此时我们可以发现,
,此时我们可以发现, 和
和 是相似三角形(
是相似三角形( 为公共角,
为公共角, )
)
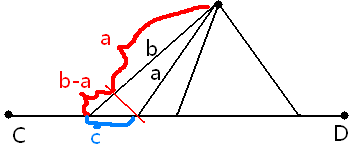
所以 和
和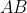 有一定的比值,即
有一定的比值,即 (AF无论如何都不应该比AB要大)
(AF无论如何都不应该比AB要大)
所以我们可以直接三分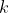 ,然后就可以求出
,然后就可以求出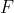 的坐标了。通过AB来求出AF。
的坐标了。通过AB来求出AF。
同样的方法三分线段 ,用三分套三分(同三分坐标的方法)。
,用三分套三分(同三分坐标的方法)。
我们找到的这个CD上的点就是与AB上的F点相连接的点。使得这个距离可以最短。
【代码实现】
#include<cmath>
#include<cstdio>
#include<cstring>
using namespace std;
struct node
{
double x,y;//x左边和y左边
}a,b,c,d; double p,q,r;
double gougu(node n1,node n2)//勾股求斜边的长度
{
return sqrt((n1.x-n2.x)*(n1.x-n2.x)+(n1.y-n2.y)*(n1.y-n2.y));
//(两个点相对应的横左边相减的平方+两个点相对应的纵坐标相减的平方)再开方
//这一步不难理解主要的目的是为了求出AF的长度
}
node find(node n1,node n2,double k)
{
node no; no.x=(n2.x-n1.x)*k+n1.x; no.y=(n2.y-n1.y)*k+n1.y;//找出F点的左边
//横左标就是AB的长度乘以比值就是AF的长度,横坐标就是加上A点的横坐标
//纵左标就是AB的长度乘以比值就是AF的长度,纵坐标就是加上A点的纵坐标
/*
可能会有疑问就是说,知道长度就好了为什么还要求左边?
因为我们知道了坐标之后,才能带入坐标求出长度啊,所以这就是为什么我们要用
三分比值来找出这个坐标的原因
*/
return no;
}
double checkjuli(double x,double y)
{
node n1=find(a,b,x),n2=find(c,d,y);//定义两点,目的是为了算出定值然后求出坐标
return gougu(a,n1)/p+gougu(n1,n2)/r+gougu(n2,d)/q;
//gougu(a,n1)/p 表示AB上的点到A的长度
//gougu(n1,n2)/r 表示AB上的点到CD上的点的长度
//gougu(n2,d)/q 表示CD上的点到D的长度
}
double check(double x)
{
double l=0.0,r=1.0;
while(r-l>=1e-7)
{
double mid1=l+(r-l)/3.0,mid2=r-(r-l)/3.0;
if(checkjuli(x,mid1)>checkjuli(x,mid2)) l=mid1;
//如果我们代入的这个点在mid1的长度>在mid2的长度说明这不是上升序列
//说明我们找到的不是最标准的最小值的上升序列
else r=mid2;
}
return checkjuli(x,l);
}
int main()
{
scanf("%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y);
scanf("%lf%lf%lf%lf",&c.x,&c.y,&d.x,&d.y);
scanf("%lf%lf%lf",&p,&q,&r);
double l=0.0,r=1.0;
while(r-l>=1e-7)
{
double mid1=l+(r-l)/3.0,mid2=r-(r-l)/3.0;
if(check(mid1)>check(mid2))l=mid1;
//这一步就是所谓的三分套三分,因为我们是先找到一个点到CD上距离最短
//然后再找一个点是CD到AB上最短的点
//然后这两个点的距离+各自到节点的距离就会使得A点到D点的距离最短
else r=mid2;
}
printf("%.2lf",check(l));//把上升序列的l再走一遍流程算出最后的长度
return 0;
}