上一篇(https://blog.csdn.net/To_be_to_thought/article/details/84668630)介绍了二叉树的性质和常用的相关的递归、非递归算法,这一篇想接着写从二叉树的遍历结果重构一棵树,主要是重构的过程思路。
1.中序遍历和先根遍历结果重构二叉树算法:
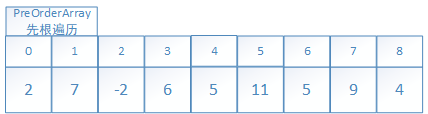
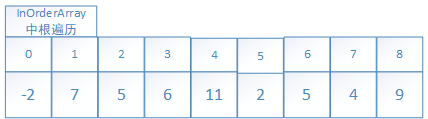
1.1回忆原始的树(以2为根节点的树)先根遍历过程和结果序列:


再看以7为根节点的子树的先根遍历过程以及结果序列:
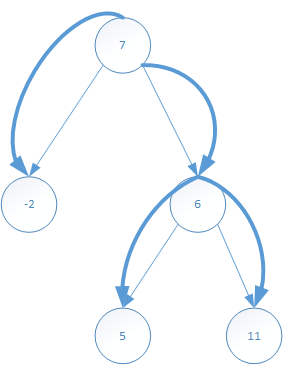
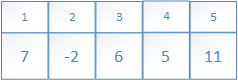
再看以5位根节点的右子树的先根遍历过程以及结果序列:
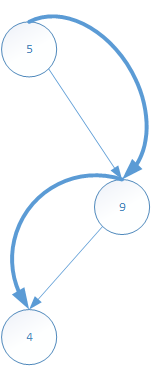

把整个递归过程表现出来,黑色表示遍历访问一棵新(子)树,红色表示访问树节点:

1.2另一方面回忆一下(以2为根节点的树)中根遍历过程和结果序列:

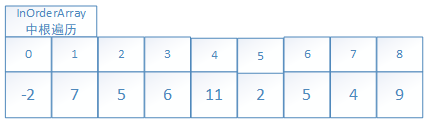
以7为根节点的左子树的中根遍历和结果序列:
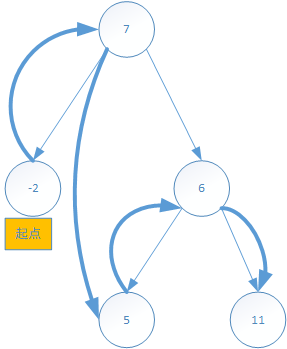
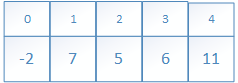
以5根节点的右子树的中根遍历和结果序列;

把整个递归过程表现出来,黑色表示遍历访问一棵新(子)树,红色只表示访问树节点,蓝色表示当前子树的根:

1.3把上述过程总结一下:
在中序遍历中找出整棵树的根节点的索引index,然后index左边序列为左子树的中序遍历,index右边序列为右子树的中序遍历。

对于这一步产生的左子树比遍历序列可以采用同样的方式继续切分:

那么应该如何切分才是最为关键的问题:
首先根节点元素在子数组中的相对位置i是可以通过在中序遍历子数组中搜索到的,子数组索引范围可以由(起点索引,终点索引)或者(起点索引,子数组长度)的二元组唯一确定:
先根遍历和中根遍历两种次序可以唯一确定二叉树,后根遍历(子)数组PostOrderArray和中根遍历子数组(子)InOrderArray长度为n
对于整棵树,先根遍历序列的起点prestart,先根遍历序列PreOrderArray的PreOrderArray[prestart]为根节点;中根遍历序列的起点为inStart,中根遍历序列的InOrderArray中寻找值等于PreOrderArray[inStart]的节点,序号为i
在InOrderArray中i左边0,i-1为左子树,i+1,n为右子树
左子树的先根遍历序列(长度为i)为PreOrderArray[preStart+1],...,PreOrderArray[preStart+i],
左子树的中根遍历序列(长度为i)为InOrderArray[inStart],...InOrderArray[i+inStart-1]
右子树的先根遍历序列(长度为n-i-1)为PreOrderArray[preStart+i+1],...PreOrderArray[n+preStart+1]
右子树的中根遍历序列(长度为n-i-1)为InOrderArray[inStart+i+1],...,InOrderArray[n+inStart-1]
有了如上归纳,不难得出如下代码:
public BinaryTree(T[] preOrderArray,T[] inOrderArray)
{
this.root=create(preOrderArray,inOrderArray,0,0,preOrderArray.length);
}
public BinaryNode<T> create(T[] preOrderArray,T[] inOrderArray,int preStart,int inStart,int n )
{
if(n<=0)
return null;
T e=preOrderArray[preStart];
BinaryNode<T> p=new BinaryNode<T>(e);
int i=0;
while(i<n && !inOrderArray[i+inStart].equals(e))
i++;
p.left=create(preOrderArray,inOrderArray,preStart+1,inStart,i);
p.right=create(preOrderArray,inOrderArray,preStart+i+1,inStart+i+1,n-1-i);
return p;
}2.后序遍历和先根遍历结果重构二叉树算法:
由于上一个例子过于详细,这个算法有点类似,关键是找切分子数组的位置。
举个例子:后根遍历和中根遍历两种次序可以唯一确定二叉树,后根遍历(子)数组PostOrderArray和中根遍历(子)数组InOrderArray长度为n,序号为0~n-1
后根遍历整个数组中PostOrderArray的PostOrderArray[n-1]为根节点,在中根遍历序列的InOrderArray中寻找值为PostOrderArray[n-1]的节点,序号为i
在InOrderArray中i左边[0:i-1]为左子树,[i+1:n]为右子树
左子树的后根遍历序列为PostOrderArrayArray[0],...,PostOrderArray[i-1]
左子树的中根遍历序列为InOrderArray[0],...InOrderArray[i-1]
右子树的后根遍历序列为PostOrderArray[i+1],...PostOrderArray[n-2]
右子树的中根遍历序列InOrderArray[i+1],...,InOrderArray[n-1]
下面进行归纳:
后根遍历和中根遍历两种次序可以唯一确定二叉树,后根遍历(子)数组PostOrderArray和中根遍历子数组(子)InOrderArray长度为n ,在原数组中的起点索引分别为inStart,postStart,终点索引分别为inStart+n-1,postStart+n-1,也就是说:PostOrderArray[postStart:postStart+n-1]和InOrderArray[inStart:inStart+n-1]对同一棵树的后根遍历和中根遍历。
后根遍历序列PostOrderArray的PostOrderArray[postStart+n-1]为根节点;在中根遍历子序列寻找值为PostOrderArray[postStart+n-1]的节点数组索引i;
左子树的后根遍历序列(长度为i)为PostOrderArray[postStart],...,PreOrderArray[postStart+i-1],
左子树的中根遍历序列(长度为i)为InOrderArray[inStart],...InOrderArray[i+inStart-1]
右子树的后根遍历序列(长度为n-i-1)为PostOrderArray[postStart+i],...PostOrderArray[postStart+n-2]
右子树的中根遍历序列(长度为n-i-1)为InOrderArray[inStart+i+1],...,InOrderArray[inStart+n-1]
可以利用起点索引和子数组长度(子树节点总数)手动来推一推上面的归纳结论:
代码如下:
public BinaryTree(T[] PostOrderArray,T[] inOrderArray)
{
this.root=create(PostOrderArray,inOrderArray,0,0,PostOrderArray.length);
}
public BinaryNode<T> create(T[] PostOrderArray,T[] inOrderArray,int postStart,int inStart,int n )
{
if(n<=0)
return null;
T e=PostOrderArray[postStart];
BinaryNode<T> p=new BinaryNode<T>(e);
int i=0;
while(i<n && !inOrderArray[i+inStart].equals(e))
i++;
p.left=create(PostOrderArray,inOrderArray,postStart,inStart,i);
p.right=create(PostOrderArray,inOrderArray,postStart+i,inStart+i+1,n-i-1);
return p;
}这大概是我写的最长的博客了,图花了好长时间才画好的!!!