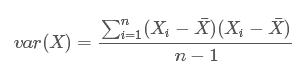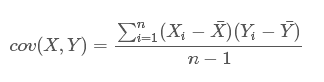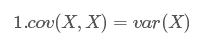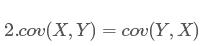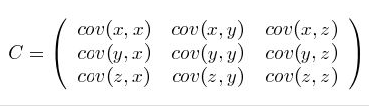目录
注意:一定是一个对称的方阵,一定是一个对称的方阵!!!记住就好啦~
最近老师讲课还有看论文的时候经常看到协方差矩阵这个破东西,自己还是搞不太清楚,查了协方差矩阵的资料,恶补之后决定马上记录下来。研究生数学1考试的概率论与数理统计有此知识,有些忘啦。
1、统计学的定义
学过概率统计的孩子都知道,统计里最基本的概念就是样本的均值,方差,或者再加个标准差。首先我们给你一个含有n个样本的集合X={X1,…,Xn},依次给出这些概念的公式描述,这些高中学过数学的孩子都应该知道吧,一带而过。
很显然,均值描述的是样本集合的中间点,它告诉我们的信息是很有限的,而标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均。以这两个集合为例,[0,8,12,20]和[8,9,11,12],两个集合的均值都是10,但显然两个集合差别是很大的,计算两者的标准差,前者是8.3,后者是1.8,显然后者较为集中,故其标准差小一些,标准差描述的就是这种“散布度”。之所以除以n-1而不是除以n,是因为这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。
那么问题来了,上面介绍的参量难道不能描述统计学所有特性吗?为啥还要搞出一个协方差出来?
上面几个统计量看似已经描述的差不多了,但我们应该注意到,标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集,最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多,,比如,一个男孩子的猥琐程度跟他受女孩子欢迎程度是否存在一些联系啊,嘿嘿~协方差就是这样一种用来度量两个随机变量关系的统计量,我们可以仿照方差的定义:
来度量各个维度偏离其均值的程度,协方差可以这么来定义:
那么,协方差的结果有什么意义呢?如果结果为正值,则说明两个随机变量是正相关的(从协方差可以引出“相关系数”的定义),也就是说一个人越猥琐就越受女孩子欢迎,嘿嘿,那必须的~结果为负值就说明负相关的,越猥琐女孩子越讨厌,可能吗?如果为0,也是就是统计上说的“相互独立”。
从协方差的定义上我们也可以看出一些显而易见的性质,如:
2、协方差矩阵的由来
好几十年前,鲁迅爷爷就说过,世界上本没有路,走的人多了也就有了路。协方差矩阵也是这样,好多协方差凑合到一起就形成了协方差矩阵。当然,数学的定义,不能如我这样随意。对于一个二维矩阵,每一个因子都可以视为两个不同随机变量的关系,这正好和协方差矩阵多少有点牵连,因此数学家们就把协方差矩阵引入到了二维矩阵中,衡量各个变量之间的紧密程度(就是关系度啦)。根据协方差的性质,我们可以类似的推出协方差矩阵的性质:
1.协方差矩阵一定是个对称的方阵
2.协方差矩阵对角线上的因子其实就是变量的方差:cov(X,X)=var(X)
这个定义还是很容易理解的,我们可以举一个简单的三变量的例子,假设数据集有{x,y,z}{x,y,z}三个维度,则协方差矩阵为:
再一次可以看出,协方差矩阵是一个对称的矩阵,而且对角线是各个变量上的方差。
3、MATLAB实战练习
上面涉及的内容都比较容易,协方差矩阵似乎也很简单,但实战起来就很容易让人迷茫了。必须要明确一点,### 协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的。
为了说明计算原理,不直接调用Matlab的cov函数:
首先,随机产生一个10*3维的整数矩阵作为样本集,10为样本的个数,3为样本的维数。
rand(3,3)是生成3*3的伪随机数矩阵,每个元素服从(0,1)的均匀分布,fix是向最近的整数取整
MySample = fix(rand(10,3)*50)
MySample =
3 8 22
2 39 4
26 15 11
38 26 45
46 8 7
6 30 41
28 13 26
23 32 49
0 34 3
16 37 22
注意:根据公式,计算协方差需要计算均值,那是按行计算均值还是按列呢,我一开始就老是困扰这个问题。前面我们也特别强调了,协方差矩阵是计算不同维度间的协方差,要时刻牢记这一点。
样本矩阵的每行是一个样本,每列为一个维度,所以我们要按列计算均值。为了描述方便,我们先将三个维度的数据分别赋值:
%A(:,j)获取矩阵第j列的全部元素,A(i,:)获取矩阵第i行的全部元素。
dim1 = MySample(:,1);
dim2 = MySample(:,2);
dim3 = MySample(:,3);计算dim1与dim2,dim1与dim3,dim2与dim3的协方差:
% .*是点乘,矩阵(向量)对应位置的元素相乘
sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( size(MySample,1)-1 ) % 得到 -92.1778
sum( (dim1-mean(dim1)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到 57.8889
sum( (dim2-mean(dim2)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到 23.2222
搞清楚了这个后面就容易多了,协方差矩阵的对角线就是各个维度上的方差,下面我们依次计算:
std(dim1)^2 % 得到 257.7333
std(dim2)^2 % 得到 145.7333
std(dim3)^2 % 得到 295.1111这样,我们就得到了计算协方差矩阵所需要的所有数据:
| C11=257.7333 | C12= -92.1778 | C13= 57.8889 |
| C21= -92.1778 | C22=145.7333 | C23=23.2222 |
| C31= 57.8889 | C32=23.2222 | C33=295.1111 |
调用Matlab自带的cov函数进行验证
| C11=257.7333 | C12= -92.1778 | C13= 57.8889 |
| C21= -92.1778 | C22=145.7333 | C23=23.2222 |
| C31= 57.8889 | C32=23.2222 | C33=295.1111 |
4、心得感悟
理解协方差矩阵的关键就在于牢记它计算的是不同维度之间的协方差,而不是不同样本之间,拿到一个样本矩阵,我们最先要明确的就是一行是一个样本还是一个维度,心中明确这个整个计算过程就会顺流而下,这么一来就不会迷茫了。其实还有一个更简单的容易记还不容易出错的方法:协方差矩阵一定是一个对称的方阵,