7. 最小生成树

一. 有权图

• 带权图即 在边上附加数据 

表示方法

• 对于邻接矩阵，只需将原来的true改为边上所附加的数据 

---

• 对于邻接表，则以增加数据的方式表示 

---

• 为了是邻接表和邻接矩阵接口统一， 边上的数据统一封装成Edge类。
• 邻接矩阵中0的地方，则以空指针表示

代码实现

• 邻接矩阵是g[w][v]存放Edge
• 邻接表是g[v]存放Edge

Edge.h

#ifndef INC_01_WEIGHTED_GRAPH_EDGE_H
#define INC_01_WEIGHTED_GRAPH_EDGE_H

#include <iostream>
#include <cassert>

using namespace std;

// 边
template<typename Weight>
class Edge{
private:
    int a,b;    // 边的两个端点  如果对于有向图， 则ab的先后表示方向
    Weight weight;  // 边的权值

public:
    // 构造函数
    Edge(int a, int b, Weight weight){
        this->a = a;
        this->b = b;
        this->weight = weight;
    }
    // 空的构造函数, 所有的成员变量都取默认值
    Edge(){}

    ~Edge(){}

    int v(){ return a;} // 返回第一个顶点
    int w(){ return b;} // 返回第二个顶点
    Weight wt(){ return weight;}    // 返回权值

    // 给定一个顶点, 返回另一个顶点
    int other(int x){
        assert( x == a || x == b );
        return x == a ? b : a;
    }

    // 输出边的信息
    friend ostream& operator<<(ostream &os, const Edge &e){
        os<<e.a<<"-"<<e.b<<": "<<e.weight;
        return os;
    }

    // 边的大小比较, 是对边的权值的大小比较
    bool operator<(Edge<Weight>& e){
        return weight < e.wt();
    }
    bool operator<=(Edge<Weight>& e){
        return weight <= e.wt();
    }
    bool operator>(Edge<Weight>& e){
        return weight > e.wt();
    }
    bool operator>=(Edge<Weight>& e){
        return weight >= e.wt();
    }
    bool operator==(Edge<Weight>& e){
        return weight == e.wt();
    }
};

#endif //INC_01_WEIGHTED_GRAPH_EDGE_H

ReadGraph.h

#ifndef INC_01_WEIGHTED_GRAPH_READGRAPH_H
#define INC_01_WEIGHTED_GRAPH_READGRAPH_H

#include <iostream>
#include <string>
#include <fstream>
#include <sstream>
#include <cassert>

using namespace std;

// 读取有权图、
template <typename Graph, typename Weight>
class ReadGraph{

public:
    // 从文件filename中读取有权图的信息, 存储进图graph中
    ReadGraph(Graph &graph, const string &filename){

        ifstream file(filename);
        string line;
        int V, E;

        assert(file.is_open());

        // 第一行读取图中的节点个数和边的个数
        assert( getline(file,line));
        stringstream ss(line);
        ss >> V >> E;
        assert( graph.V() == V );

        // 读取每一条边的信息
        for( int i = 0 ; i < E ; i ++ ){
            assert( getline(file,line));
            stringstream ss(line);

            int a, b;
            Weight w;
            ss>>a>>b>>w;
            assert( a >= 0 && a < V );
            assert( b >= 0 && b < V );
            graph.addEdge(a, b, w);
        }

    }
};

#endif //INC_01_WEIGHTED_GRAPH_READGRAPH_H

DenseGraph.h 稠密图邻接矩阵

#ifndef INC_01_WEIGHTED_GRAPH_DENSEGRAPH_H
#define INC_01_WEIGHTED_GRAPH_DENSEGRAPH_H

#include <iostream>
#include <vector>
#include <cassert>
#include "Edge.h"

using namespace std;

// 稠密图 - 邻接矩阵
template <typename Weight>
class DenseGraph{

private:
    int n, m;       // 节点数和边数
    bool directed;  // 是否为有向图
    vector<vector<Edge<Weight> *>> g;   // 图的具体数据

public:
    // 构造函数
    DenseGraph( int n , bool directed){
        assert( n >= 0 );
        this->n = n;
        this->m = 0;
        this->directed = directed;
        // g初始化为n*n的矩阵, 每一个g[i][j]指向一个边的信息, 初始化为NULL
        g = vector<vector<Edge<Weight> *>>(n, vector<Edge<Weight> *>(n, NULL));
    }

    // 析构函数
    ~DenseGraph(){

        for( int i = 0 ; i < n ; i ++ )
            for( int j = 0 ; j < n ; j ++ )
                if( g[i][j] != NULL )
                    delete g[i][j];
    }

    int V(){ return n;} // 返回节点个数
    int E(){ return m;} // 返回边的个数

    // 向图中添加一个边, 权值为weight
    void addEdge( int v, int w , Weight weight ){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );

        // 如果从v到w已经有边, 删除这条边
        if( hasEdge( v , w  ) ){
            delete  g[v][w];
            if( v != w && !directed ) // 无向图  g[w][v]也删除
                delete g[w][v];
            m --;
        }

        g[v][w] = new Edge<Weight>(v, w, weight);
        if( v != w && !directed )
            g[w][v] = new Edge<Weight>(w, v, weight);
        m ++;
    }

    // 验证图中是否有从v到w的边
    bool hasEdge( int v , int w ){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
        return g[v][w] != NULL;
    }

    // 显示图的信息
    void show(){

        for( int i = 0 ; i < n ; i ++ ){
            for( int j = 0 ; j < n ; j ++ )
                if( g[i][j] )
                    cout<<g[i][j]->wt()<<"\t";
                else
                    cout<<"NULL\t";
            cout<<endl;
        }
    }

    // 邻边迭代器, 传入一个图和一个顶点,
    // 迭代在这个图中和这个顶点向连的所有边
    class adjIterator{
    private:
        DenseGraph &G;  // 图G的引用
        int v;
        int index;

    public:
        // 构造函数
        adjIterator(DenseGraph &graph, int v): G(graph){
            this->v = v;
            this->index = -1;   // 索引从-1开始, 因为每次遍历都需要调用一次next()
        }

        ~adjIterator(){}

        // 返回图G中与顶点v相连接的第一个边
        Edge<Weight>* begin(){
            // 索引从-1开始, 因为每次遍历都需要调用一次next()
            index = -1;
            return next();
        }

        // 返回图G中与顶点v相连接的下一个边
        Edge<Weight>* next(){
            // 从当前index开始向后搜索, 直到找到一个g[v][index]为true
            for( index += 1 ; index < G.V() ; index ++ )
                if( G.g[v][index] )
                    return G.g[v][index];
            // 若没有顶点和v相连接, 则返回NULL
            return NULL;
        }

        // 查看是否已经迭代完了图G中与顶点v相连接的所有边
        bool end(){
            return index >= G.V();
        }
    };
};

#endif //INC_01_WEIGHTED_GRAPH_DENSEGRAPH_H

SparseGraph.h 稀疏图邻接表

#ifndef INC_01_WEIGHTED_GRAPH_SPARSEGRAPH_H
#define INC_01_WEIGHTED_GRAPH_SPARSEGRAPH_H

#include <iostream>
#include <vector>
#include <cassert>
#include "Edge.h"

using namespace std;

// 稀疏图 - 邻接表
template<typename Weight>
class SparseGraph{

private:
    int n, m;       // 节点数和边数
    bool directed;  // 是否为有向图
    vector<vector<Edge<Weight> *> > g;   // 图的具体数据

public:
    // 构造函数
    SparseGraph( int n , bool directed){
        assert(n >= 0);
        this->n = n;
        this->m = 0;    // 初始化没有任何边
        this->directed = directed;
        // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
        g = vector<vector<Edge<Weight> *> >(n, vector<Edge<Weight> *>());
    }

    // 析构函数
    ~SparseGraph(){
        for( int i = 0 ; i < n ; i ++ )
            for( int j = 0 ; j < g[i].size() ; j ++ )
                delete g[i][j];
    }

    int V(){ return n;} // 返回节点个数
    int E(){ return m;} // 返回边的个数

    // 向图中添加一个边, 权值为weight
    void addEdge( int v, int w , Weight weight){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );

        // 注意, 由于在邻接表的情况, 查找是否有重边需要遍历整个链表
        // 我们的程序允许重边的出现

        g[v].push_back(new Edge<Weight>(v, w, weight));
        if( v != w && !directed )
            g[w].push_back(new Edge<Weight>(w, v, weight));
        m ++;
    }

    // 验证图中是否有从v到w的边
    bool hasEdge( int v , int w ){
        assert( v >= 0 && v < n );
        assert( w >= 0 && w < n );
        for( int i = 0 ; i < g[v].size() ; i ++ )
            if( g[v][i]->other(v) == w )
                return true;
        return false;
    }

    // 显示图的信息
    void show(){

        for( int i = 0 ; i < n ; i ++ ){
            cout<<"vertex "<<i<<":\t";
            for( int j = 0 ; j < g[i].size() ; j ++ )
                cout<<"( to:"<<g[i][j]->w()<<",wt:"<<g[i][j]->wt()<<")\t";
            cout<<endl;
        }
    }

    // 邻边迭代器, 传入一个图和一个顶点,
    // 迭代在这个图中和这个顶点向连的所有边
    class adjIterator{
    private:
        SparseGraph &G; // 图G的引用
        int v;
        int index;

    public:
        // 构造函数
        adjIterator(SparseGraph &graph, int v): G(graph){
            this->v = v;
            this->index = 0;
        }

        ~adjIterator(){}

        // 返回图G中与顶点v相连接的第一个边
        Edge<Weight>* begin(){
            index = 0;
            if( G.g[v].size() )
                return G.g[v][index];
            // 若没有顶点和v相连接, 则返回NULL
            return NULL;
        }

        // 返回图G中与顶点v相连接的下一个边
        Edge<Weight>* next(){
            index += 1;
            if( index < G.g[v].size() )
                return G.g[v][index];
            return NULL;
        }

        // 查看是否已经迭代完了图G中与顶点v相连接的所有顶点
        bool end(){
            return index >= G.g[v].size();
        }
    };
};

#endif //INC_01_WEIGHTED_GRAPH_SPARSEGRAPH_H

测试文件testG1.txt

8 16
4 5 .35
4 7 .37
5 7 .28
0 7 .16
1 5 .32
0 4 .38
2 3 .17
1 7 .19
0 2 .26
1 2 .36
1 3 .29
2 7 .34
6 2 .40
3 6 .52
6 0 .58
6 4 .93

main.cpp

#include <iostream>
#include <iomanip>
#include "DenseGraph.h"
#include "SparseGraph.h"
#include "ReadGraph.h"

using namespace std;

// 测试有权图和有权图的读取
int main() {

    string filename = "testG1.txt";
    int V = 8;
    cout<<fixed<<setprecision(2);

    // Test Weighted Dense Graph
    DenseGraph<double> g1 = DenseGraph<double>(V, false);
    ReadGraph<DenseGraph<double>,double> readGraph1(g1, filename);
    g1.show();
    cout<<endl;

    // Test Weighted Sparse Graph
    SparseGraph<double> g2 = SparseGraph<double>(V, false);
    ReadGraph<SparseGraph<double>,double> readGraph2(g2, filename);
    g2.show();
    cout<<endl;

    return 0;
}

---

二. 最小生成树问题和切分定理

最小生成树

• 一个有v个节点的图， 用v-1条边，连通所有节点， 并且使得这些边上的权重加起来最小
• 针对带权无向图(前置条件)
• 针对连通图(前置条件)

---

应用

• 电缆布线设计
• 网络设计
• 电路设计

---

切分定理

• 切分： 把图中的节点分为两部分成为一个切分
• 横切边： 如果一个边的两个端点， 属于切分的不同的两边， 这个边称为横切边
• 切分定理： 给定任意切分， 横切边中权值最小的边必然属于最小生成树

---

三. Prim算法的第一个实现 (Lazy Prim)

过程描述

---

1. 取第一个点  0， 0和其他点分为了两部分， 成为一个切分
    将横切边 放入最小堆， 得到最短的横切边 0-7， 0-7从最小堆中移除

2. 新切分由  0-7  和其他点 构成，
    将横切边放入最小堆(原来在堆中的边不会被丢掉)， 得到最短横切边 1-7, 1-7从最小堆中移除

3. 新切分由 0-7-1 和其他点 构成,
    将横切边放入最小堆(原来在堆中的边不会被丢掉)， 得到最短横切边 0-2, 0-2从最小堆中移除

4. 新切分由 0-7-1-2 和其他点 构成,
    将横切边放入最小堆(原来在堆中的边不会被丢掉)， 得到最短横切边 2-3, 2-3从最小堆中移除

5. 新切分由 0-7-1-2-3 和其他点 构成,
    将横切边放入最小堆(原来在堆中的边不会被丢掉)， 得到最短横切边 5-7, 5-7从最小堆中移除
    
6. 新切分由 0-7-1-2-3-5 和其他点 构成,
    将横切边放入最小堆(原来在堆中的边不会被丢掉)， 得到堆中最短边 1-3, 1-3不是横切边(通过1-3 在同一侧的切分来判断), 从堆中移除。继续得到最短边1-5， 依然不是横切边， 移除。 得到最短边4-5，是横切边， 从堆中获取后移除。

7. 新切分由 0-7-1-2-3-5-4 和其他点 构成,
    重复6的步骤， 得到最短横切边2-6

8. 新切分由 0-7-1-2-3-5-4-6 和其他点 构成(其实此时已经没有其他点),
    从堆中找出最短边， 发现都不是横切边。。。直到堆中无数据， 程序结束

代码实现

• LazyPrim.h

#ifndef INC_03_LAZY_PRIM_LAZYPRIMMST_H
#define INC_03_LAZY_PRIM_LAZYPRIMMST_H

#include <iostream>
#include <vector>
#include <cassert>
#include "Edge.h"
#include "MinHeap.h"

using namespace std;

// 使用Prim算法求图的最小生成树
template<typename Graph, typename Weight>
class LazyPrimMST{

private:
    Graph &G;                   // 图的引用
    MinHeap<Edge<Weight>> pq;   // 最小堆, 算法辅助数据结构
    bool *marked;               // 标记数组, 在算法运行过程中标记节点i是否已经是是  总是在增加节点的那一边的切分
    vector<Edge<Weight>> mst;   // 最小生成树所包含的所有边
    Weight mstWeight;           // 最小生成树的权值

    // 访问节点v
    void visit(int v){

        assert( !marked[v] );
        marked[v] = true;

        // 将和节点v相连接的所有未访问的边放入最小堆中
        typename Graph::adjIterator adj(G,v);
        for( Edge<Weight>* e = adj.begin() ; !adj.end() ; e = adj.next() )
            if( !marked[e->other(v)] )  
                pq.insert(*e);
    }

public:
    // 构造函数, 使用Prim算法求图的最小生成树
    LazyPrimMST(Graph &graph):G(graph), pq(MinHeap<Edge<Weight>>(graph.E())){

        // 算法初始化
        marked = new bool[G.V()];
        for( int i = 0 ; i < G.V() ; i ++ )
            marked[i] = false;
        mst.clear();

        // Lazy Prim
        visit(0);
        while( !pq.isEmpty() ){
            // 使用最小堆找出已经访问的边中权值最小的边
            Edge<Weight> e = pq.extractMin();
            // 如果这条边的两端不构成横切边, 则扔掉这条边
            if( marked[e.v()] == marked[e.w()] )
                continue;
            // 否则, 这条边则应该存在在最小生成树中
            mst.push_back( e );

            // 访问和这条边连接的还没有被访问过的节点， 放入横切边
            if( !marked[e.v()] )
                visit( e.v() );
            else
                visit( e.w() );
        }

        // 计算最小生成树的权值
        mstWeight = mst[0].wt();
        for( int i = 1 ; i < mst.size() ; i ++ )
            mstWeight += mst[i].wt();
    }

    // 析构函数
    ~LazyPrimMST(){
        delete[] marked;
    }

    // 返回最小生成树的所有边
    vector<Edge<Weight>> mstEdges(){
        return mst;
    };

    // 返回最小生成树的权值
    Weight result(){
        return mstWeight;
    };
};

#endif //INC_03_LAZY_PRIM_LAZYPRIMMST_H

• 测试main.cpp

#include <iostream>
#include <iomanip>
#include "DenseGraph.h"
#include "SparseGraph.h"
#include "ReadGraph.h"
#include "LazyPrimMST.h"

using namespace std;

// 测试最小生成树算法
int main() {

    string filename = "testG1.txt";
    int V = 8;

    SparseGraph<double> g = SparseGraph<double>(V, false);
    ReadGraph<SparseGraph<double>, double> readGraph(g, filename);

    // Test Lazy Prim MST
    cout<<"Test Lazy Prim MST:"<<endl;
    LazyPrimMST<SparseGraph<double>, double> lazyPrimMST(g);
    vector<Edge<double>> mst = lazyPrimMST.mstEdges();
    for( int i = 0 ; i < mst.size() ; i ++ )
        cout<<mst[i]<<endl;
    cout<<"The MST weight is: "<<lazyPrimMST.result()<<endl;

    cout<<endl;

    return 0;
}

---

四. Prim算法的优化

思路

• 使用最小索引堆，存放每个节点的最小横切边

---

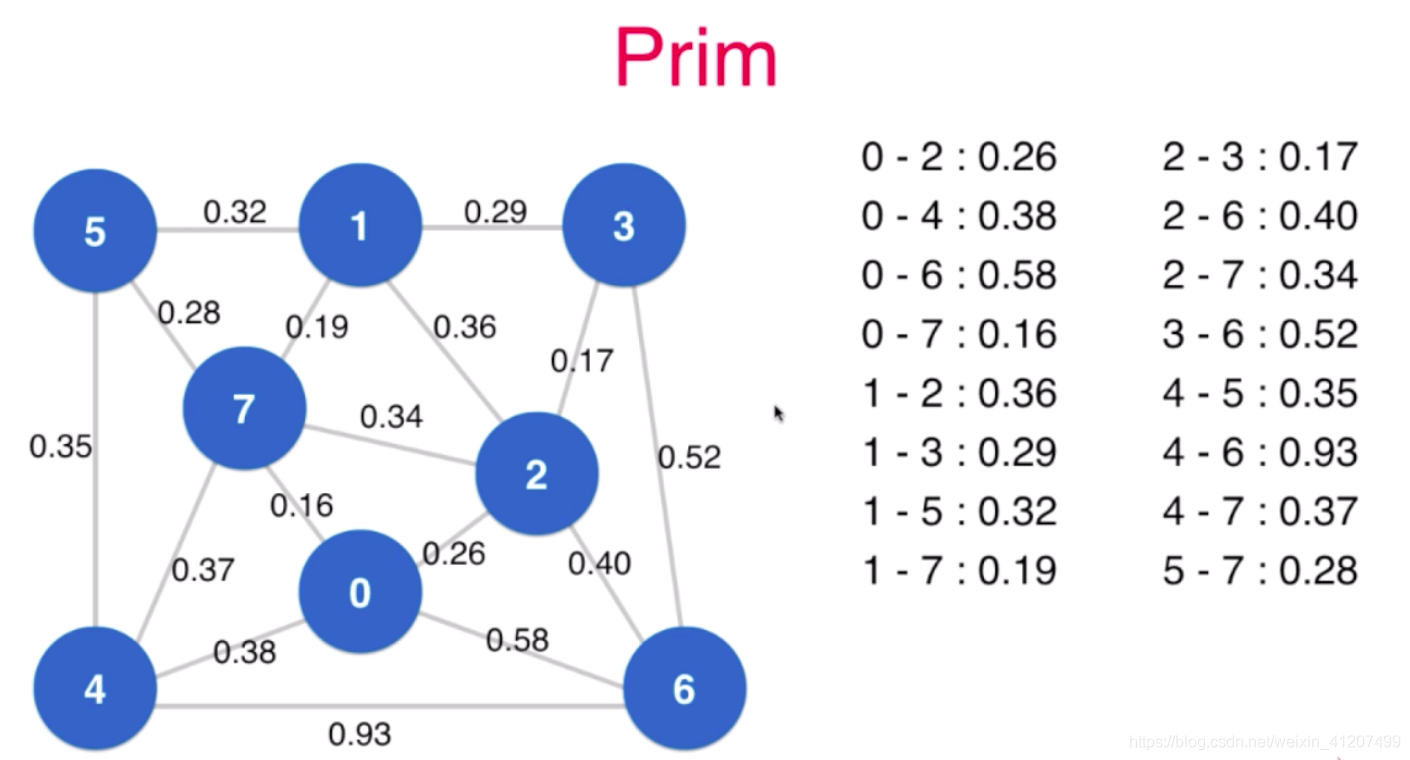
步骤1.    先取一点， 这里取0， 将和0相连的节点， 在最小索引堆中记录0的横切边，并找到最小横切边0.16
mark标记的 不在寻找最小横切边的范围内
mark
 0     1      2       3       4       5       6       7
 -     -     0.26     -      0.38     -      0.58    0.16
 

步骤2.    更新切分 0-7 , 遍历和7相连的横切边，更新最小索引堆(7-4比原来的0-4小，更新4为0.37)。 最小边为1的0.19
mark                                                mark
 0     1       2      3       4        5       6      7
 -    0.19   0.26     -      0.37    0.28    0.58    0.16


步骤3.  更新切分 0-7-1, 遍历和1相连的横切边， 更新最小索引堆(1-3,更新3)。 最小横切边为2的0.26
mark   mark                                         mark
 0     1       2      3       4        5       6      7
 -    0.19   0.26    0.29    0.37    0.28    0.58    0.16
 
步骤4.  更新切分 0-7-1-2, 遍历和2相连的横切边， 更新最小索引堆(2-3小于1-3，更新为0.17)。 最小横切边为2的0.26
mark   mark   mark                                  mark
 0     1       2      3       4        5       6      7
 -    0.19   0.26    0.17    0.37    0.28    0.40    0.16
 

... 重复以上步骤， 直到全部mark

代码实现

• 最小索引堆 IndexMinHeap.h

#ifndef INC_05_IMPLEMENTATION_OF_OPTIMIZED_PRIM_ALGORITHM_INDEXMINHEAP_H
#define INC_05_IMPLEMENTATION_OF_OPTIMIZED_PRIM_ALGORITHM_INDEXMINHEAP_H

#include <iostream>
#include <algorithm>
#include <cassert>

using namespace std;

// 最小索引堆
template<typename Item>
class IndexMinHeap{

private:
    Item *data;     // 最小索引堆中的数据
    int *indexes;   // 最小索引堆中的索引, indexes[x] = i 表示索引i在x的位置
    int *reverse;   // 最小索引堆中的反向索引, reverse[i] = x 表示索引i在x的位置

    int count;
    int capacity;

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    void shiftUp( int k ){

        while( k > 1 && data[indexes[k/2]] > data[indexes[k]] ){
            swap( indexes[k/2] , indexes[k] );
            reverse[indexes[k/2]] = k/2;
            reverse[indexes[k]] = k;
            k /= 2;
        }
    }

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    void shiftDown( int k ){

        while( 2*k <= count ){
            int j = 2*k;
            if( j + 1 <= count && data[indexes[j]] > data[indexes[j+1]] )
                j += 1;

            if( data[indexes[k]] <= data[indexes[j]] )
                break;

            swap( indexes[k] , indexes[j] );
            reverse[indexes[k]] = k;
            reverse[indexes[j]] = j;
            k = j;
        }
    }

public:
    // 构造函数, 构造一个空的索引堆, 可容纳capacity个元素
    IndexMinHeap(int capacity){

        data = new Item[capacity+1];
        indexes = new int[capacity+1];
        reverse = new int[capacity+1];

        for( int i = 0 ; i <= capacity ; i ++ )
            reverse[i] = 0;

        count = 0;
        this->capacity = capacity;
    }

    ~IndexMinHeap(){
        delete[] data;
        delete[] indexes;
        delete[] reverse;
    }

    // 返回索引堆中的元素个数
    int size(){
        return count;
    }

    // 返回一个布尔值, 表示索引堆中是否为空
    bool isEmpty(){
        return count == 0;
    }

    // 向最小索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
    // 传入的i对用户而言,是从0索引的
    void insert(int index, Item item){
        assert( count + 1 <= capacity );
        assert( index + 1 >= 1 && index + 1 <= capacity );

        index += 1;
        data[index] = item;
        indexes[count+1] = index;
        reverse[index] = count+1;
        count++;
        shiftUp(count);
    }

    // 从最小索引堆中取出堆顶元素, 即索引堆中所存储的最小数据
    Item extractMin(){
        assert( count > 0 );

        Item ret = data[indexes[1]];
        swap( indexes[1] , indexes[count] );
        reverse[indexes[count]] = 0;
        reverse[indexes[1]] = 1;
        count--;
        shiftDown(1);
        return ret;
    }

    // 从最小索引堆中取出堆顶元素的索引
    int extractMinIndex(){
        assert( count > 0 );

        int ret = indexes[1] - 1;
        swap( indexes[1] , indexes[count] );
        reverse[indexes[count]] = 0;
        reverse[indexes[1]] = 1;
        count--;
        shiftDown(1);
        return ret;
    }

    // 获取最小索引堆中的堆顶元素
    Item getMin(){
        assert( count > 0 );
        return data[indexes[1]];
    }

    // 获取最小索引堆中的堆顶元素的索引
    int getMinIndex(){
        assert( count > 0 );
        return indexes[1]-1;
    }

    // 看索引i所在的位置是否存在元素
    bool contain( int index ){

        return reverse[index+1] != 0;
    }

    // 获取最小索引堆中索引为i的元素
    Item getItem( int index ){
        assert( contain(index) );
        return data[index+1];
    }

    // 将最小索引堆中索引为i的元素修改为newItem
    void change( int index , Item newItem ){

        assert( contain(index) );
        index += 1;
        data[index] = newItem;

        shiftUp( reverse[index] );
        shiftDown( reverse[index] );
    }

};

#endif //INC_05_IMPLEMENTATION_OF_OPTIMIZED_PRIM_ALGORITHM_INDEXMINHEAP_H

• Prim算法 PrimMST.h

#ifndef INC_05_IMPLEMENTATION_OF_OPTIMIZED_PRIM_ALGORITHM_PRIMMST_H
#define INC_05_IMPLEMENTATION_OF_OPTIMIZED_PRIM_ALGORITHM_PRIMMST_H

#include <iostream>
#include <vector>
#include <cassert>
#include "Edge.h"
#include "IndexMinHeap.h"

using namespace std;

// 使用优化的Prim算法求图的最小生成树
template<typename Graph, typename Weight>
class PrimMST{

private:
    Graph &G;                     // 图的引用
    IndexMinHeap<Weight> ipq;     // 最小索引堆, 算法辅助数据结构
    vector<Edge<Weight>*> edgeTo; // 访问的点所对应的边, 算法辅助数据结构
    bool* marked;                 // 标记数组, 在算法运行过程中标记节点i是否被访问
    vector<Edge<Weight>> mst;     // 最小生成树所包含的所有边
    Weight mstWeight;             // 最小生成树的权值

    // 访问节点v
    void visit(int v){

        assert( !marked[v] );
        marked[v] = true;

        // 将和节点v相连接的未访问的另一端点, 和与之相连接的边, 放入最小堆中
        typename Graph::adjIterator adj(G,v);
        for( Edge<Weight>* e = adj.begin() ; !adj.end() ; e = adj.next() ){
            int w = e->other(v);
            // 如果边的另一端点未被访问
            if( !marked[w] ){
                // 如果从没有考虑过这个端点, 直接将这个端点和与之相连接的边加入索引堆
                if( !edgeTo[w] ){
                    edgeTo[w] = e;
                    ipq.insert(w, e->wt()); // 最小索引堆中放入 索引和权值
                }
                // 如果曾经考虑这个端点, 但现在的边比之前考虑的边更短, 则进行替换
                else if( e->wt() < edgeTo[w]->wt() ){
                    edgeTo[w] = e;
                    ipq.change(w, e->wt());
                }
            }
        }

    }
public:
    // 构造函数, 使用Prim算法求图的最小生成树
    PrimMST(Graph &graph):G(graph), ipq(IndexMinHeap<double>(graph.V())){

        assert( graph.E() >= 1 );

        // 算法初始化
        marked = new bool[G.V()];
        for( int i = 0 ; i < G.V() ; i ++ ){
            marked[i] = false;
            edgeTo.push_back(NULL);
        }
        mst.clear();

        // Prim
        visit(0);
        while( !ipq.isEmpty() ){
            // 使用最小索引堆找出已经访问的边中权值最小的边
            // 最小索引堆中存储的是点的索引, 通过点的索引找到相对应的边
            int v = ipq.extractMinIndex();   // 从堆中取出 最小权值对应的 节点索引
            assert( edgeTo[v] );
            mst.push_back( *edgeTo[v] );
            visit( v ); // visit切分中加入的新节点
        }

        mstWeight = mst[0].wt();
        for( int i = 1 ; i < mst.size() ; i ++ )
            mstWeight += mst[i].wt();
    }

    ~PrimMST(){
        delete[] marked;
    }

    vector<Edge<Weight>> mstEdges(){
        return mst;
    };

    Weight result(){
        return mstWeight;
    };
};

#endif //INC_05_IMPLEMENTATION_OF_OPTIMIZED_PRIM_ALGORITHM_PRIMMST_H

• 测试代码

// Test Prim MST
    cout<<"Test Prim MST:"<<endl;
    PrimMST<SparseGraph<double>, double> primMST(g);
    mst = primMST.mstEdges();
    for( int i = 0 ; i < mst.size() ; i ++ )
        cout<<mst[i]<<endl;
    cout<<"The MST weight is: "<<primMST.result()<<endl;

    cout<<endl;

---

五. Krusk算法

步骤

1. 对所有的边进行从小到大的排序
2. 先取最小边
3. 接着取下一条边，如果该边与之前的所有取出的边构成了环， 则丢弃这条边
4. 重复第3步， 直到遍历过所有的边， 这样就获取了最小生成树

疑惑

1. 为什么不用marked[]数组来标记krusk算法中已经标记过的点？ 这样不就不用判断是否形成环了？

• 答： 比如1和2连起来了， 3和4连起来了， 现在1 2 3 4都遍历过了， 但它们并没有构成环

---

1. 怎样判断已经取出的边是否构成环？

• 答： 使用UnionFind 并查集这种数据结构来实现， 假如新取出了一条边，有两个顶点a和b, 先判断UnionFind中，a和b是否联通(是否有同一个root)， 联通的话就将这条边舍弃，不联通则在并查集中联通a和b两个点

---

代码实现

Krusk.h

#ifndef INC_06_KRUSKAL_ALGORITHM_KRUSKALMST_H
#define INC_06_KRUSKAL_ALGORITHM_KRUSKALMST_H

#include <iostream>
#include <vector>
#include "MinHeap.h"
#include "UF.h"
#include "Edge.h"

using namespace std;

// Kruskal算法
template <typename Graph, typename Weight>
class KruskalMST{

private:
    vector<Edge<Weight>> mst;   // 最小生成树所包含的所有边
    Weight mstWeight;           // 最小生成树的权值

public:
    // 构造函数, 使用Kruskal算法计算graph的最小生成树
    KruskalMST(Graph &graph){

        // 将图中的所有边存放到一个最小堆中
        MinHeap<Edge<Weight>> pq( graph.E() );  //利用堆排序
        for( int i = 0 ; i < graph.V() ; i ++ ){
            typename Graph::adjIterator adj(graph,i);
            for( Edge<Weight> *e = adj.begin() ; !adj.end() ; e = adj.next() )
                if( e->v() < e->w() )  // 12 这条边 同时也是21这条边， 这样避免重复
                    pq.insert(*e);
        }

        // 创建一个并查集, 来查看已经访问的节点的联通情况
        UnionFind uf = UnionFind(graph.V()); // 并查集开辟 图的顶点个数的空间节点， 每个节点一开始root都是自己
        while( !pq.isEmpty() && mst.size() < graph.V() - 1 ){

            // 从最小堆中依次从小到大取出所有的边
            Edge<Weight> e = pq.extractMin();
            // 如果该边的两个端点是联通的, 说明加入这条边将产生环, 扔掉这条边
            if( uf.isConnected( e.v() , e.w() ) )
                continue;

            // 否则, 将这条边添加进最小生成树, 同时标记边的两个端点联通
            mst.push_back( e );
            uf.unionElements( e.v() , e.w() );
        }

        mstWeight = mst[0].wt();
        for( int i = 1 ; i < mst.size() ; i ++ )
            mstWeight += mst[i].wt();
    }

    ~KruskalMST(){ }

    // 返回最小生成树的所有边
    vector<Edge<Weight>> mstEdges(){
        return mst;
    };

    // 返回最小生成树的权值
    Weight result(){
        return mstWeight;
    };
};

#endif //INC_06_KRUSKAL_ALGORITHM_KRUSKALMST_H

• 并查集代码 UF.h

#ifndef INC_06_KRUSKAL_ALGORITHM_UF_H
#define INC_06_KRUSKAL_ALGORITHM_UF_H

#include <iostream>
#include <cassert>

using namespace std;

// Quick Union + rank + path compression
class UnionFind{

private:
    // rank[i]表示以i为根的集合所表示的树的层数
    // 在后续的代码中, 我们并不会维护rank的语意, 也就是rank的值在路径压缩的过程中, 有可能不在是树的层数值
    // 这也是我们的rank不叫height或者depth的原因, 他只是作为比较的一个标准
    // 关于这个问题，可以参考问答区：http://coding.imooc.com/learn/questiondetail/7287.html
    int* rank;
    int* parent; // parent[i]表示第i个元素所指向的父节点
    int count;   // 数据个数

public:
    // 构造函数
    UnionFind(int count){
        parent = new int[count];
        rank = new int[count];
        this->count = count;
        for( int i = 0 ; i < count ; i ++ ){
            parent[i] = i;
            rank[i] = 1;
        }
    }

    // 析构函数
    ~UnionFind(){
        delete[] parent;
        delete[] rank;
    }

    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    int find(int p){
        assert( p >= 0 && p < count );

        // path compression 1
        while( p != parent[p] ){
            parent[p] = parent[parent[p]];
            p = parent[p];
        }
        return p;

        // path compression 2, 递归算法
//            if( p != parent[p] )
//                parent[p] = find( parent[p] );
//            return parent[p];
    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    bool isConnected( int p , int q ){
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    void unionElements(int p, int q){

        int pRoot = find(p);
        int qRoot = find(q);

        if( pRoot == qRoot )
            return;

        // 根据两个元素所在树的元素个数不同判断合并方向
        // 将元素个数少的集合合并到元素个数多的集合上
        if( rank[pRoot] < rank[qRoot] ){
            parent[pRoot] = qRoot;
        }
        else if( rank[qRoot] < rank[pRoot]){
            parent[qRoot] = pRoot;
        }
        else{ // rank[pRoot] == rank[qRoot]
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;   // 此时, 我维护rank的值
        }
    }
};

#endif //INC_06_KRUSKAL_ALGORITHM_UF_H