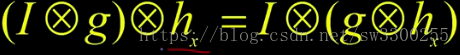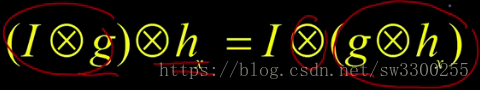目录
回顾
高斯滤波器2D的导数
Sigma对导数的影响
回顾
我们要完成我们的边缘检测这个单元,然后它会被用在你以后要做的事情上。
上单元我们讲了边的概念以及它们是如何与梯度和函数导数的大小相关的。
我们还记得,如果你大脑的某个部分脱落了,应该是梯度是什么。
我们讨论过开发一些运算,你可以应用到图像中去计算这些梯度。
我们展示了它们是如何对噪音敏感的,我们不得不担心滤波器以平滑这些东西。
我们讨论过,我们可以首先过滤图像。然后应用运算。或者我们可以先过滤操作。
抱歉,我们可以平滑运算并将其应用到图像上。
这是一幅图,它提醒我们这样做:
这是函数f。这是平滑滤波器。对它求导。
从那以后,我们可以用这个算子来求出这些峰和边。
高斯滤波器2D的导数
当然,在2D中,它不仅仅是一个导数我们还要讨论导数的方向。
在梯度,我们有x方向的导数和y方向的导数。
所以当你用同样的方法求滤波器的导数时,我们要问,在哪个方向上求导?
我们是这样写的:
我们要做的是,假设我们要对x方向求导。
这个小 (图中红色线) 意味着这是一个小滤波器它只对x方向求导。也许它是一个Sobel运算符,也许它是另外一个。
但它是一个求导的小滤波器。()
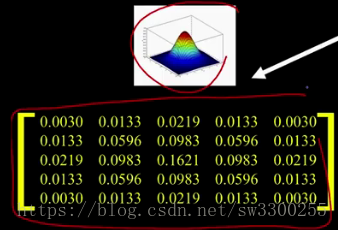
g是高斯函数,看图:
正如我们之前所说的,由于关联属性,除了平滑然后取导数之外,我们可以应用一个高斯算子及其导数:
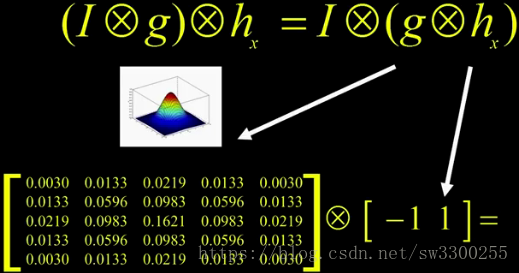
这就是这里显示的:
而- 1 1,这是一个平凡的,它可以是- 1 0 1,它是一般的导数算子。
而g,这是我的高斯函数,很平滑的,我从矩阵中取出一大块,就像这样:
这给了我们什么?
这个函数就是这样的:
这就是说,它是高斯的第一个导数,当我应用于图像时,它为我提供了高斯平滑图像的导数,用于之前的关联属性。
所以问题是,这样做是否更好。我们应该把它当成一个小测验。
因为这更可取。
小测验:
为什么对平滑函数应用h更好,h是我们的导数,然后应用这个结果?
A、嗯,它不是。他们在数学上等价的。
B、因为h通常更小,我们取更少的导数,所以它更快。
C、光滑的导数运算符计算一次重复使用;
D、B和C。
答案:D。A是正确的,但与此无关。是的,它们在数学上是等价的,但我只是说,你为什么喜欢其中一个?
B和C都是可能的原因。我想要梯度和x方向。这是我的滤镜,我就用它。这让计算变得更简单。
你知道,往前,你可能已经决定你已经有了不同的平滑图像,而你只是采用渐变,所以你直接这样做。
Sigma对导数的影响
就像我说的,当你这样做的时候,你会得到这个梯度函数。
当然,我们在x方向和y方向都这样做:
我们现在有了相关性和卷积的问题。
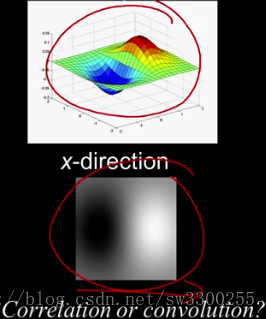
如果这是x方向,如果x向这个方向正,这是一个相关滤波器。顺便说一下,这张图就是这张图的样子:
所以外面的这些0值,就是这些灰色的,负的是负的,正的是正的:
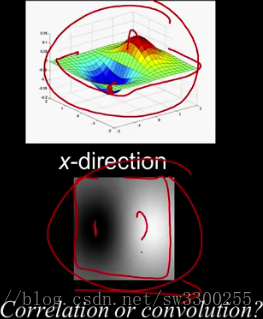
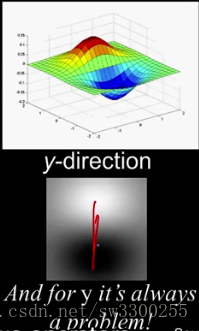
在y方向上,哪个方向是正的总是一个问题,因为,就像我们说的,y可以向上或者向下。
你知道的,主要的问题是,它,它,它是垂直的:
以上就是这两个算子。
这就是用高斯函数得到光滑导数的方法。
但有一个问题是高斯函数的大小是多少?
你们可能还记得,通过滤波我们可以选择不同大小的高斯分布,这里是fspecial,用来得到不同的Sigma。
>> for sigma = 1:3:10
h = fspecial('gaussian', fsize, sigma);
out = imfilter(im, h);
imshow(out);
pause;
end
>>代码运行结果:
这里显示的结果就是,你会得到或多或少平滑的图像。
当我们计算导数时也是一样的。
我们可以改变高斯函数的Sigma大小。
当你这样做的时候,你会得到某种程度的增强,这些导数的大小作为图像在空间中变化的速度的函数。
有了一个小的sigma,所有这些精细的纹理在这里随处可见:
事实上,即使是这个小纹理也会出现在这里:
但如果我用更大的sigma呢?
所以这个区域你可以看到这里的变化少了很多,因为我们平滑了大部分的小变化:
我们可以这样想,更小的值,更精细的特征会被检测到,更大的值,只有更大的边缘会被检测到。
——学会编写自己的代码,才能练出真功夫。