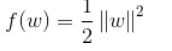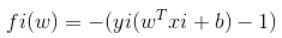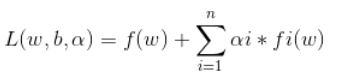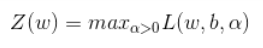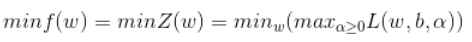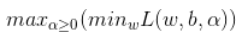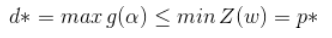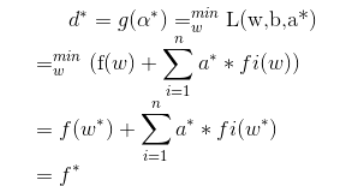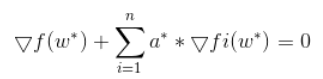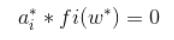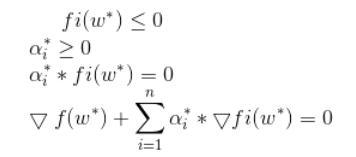在上一节支持向量机公式推导中,我们有一些公式只是给出了结果,却没有解释如何得来的,这一节我们将探讨如何将原始问题转为对偶问题,并推导出KKT条件。
1、KKT条件
对于下图所示的不等式约束优化问题,
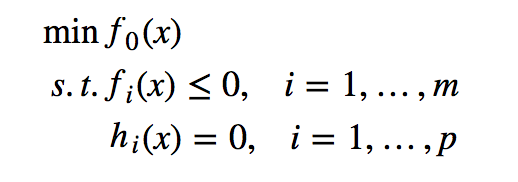
其KKT条件如以下形式:

KKT条件是解决最优化问题的时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值。下面我们开始探讨。
2、向对偶问题转化
上一节中我们得到凸优化问题
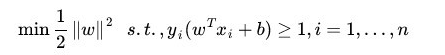
解决了这个问题即可求出最大间隔,求出超平面。
利用拉格朗日法,我们构造了函数为
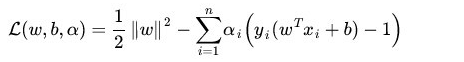
这里我们令
i=1,2,…n
则原式变为
令
因为ai>=0(上图公式里写错),fi(w)由约束条件知fi(w)<=0,故ai*fi(w)<=0,可知当取最大值时,ai或fi(w)=0时满足。此时只剩f(w)项。
即Z(w)=f(w), minf(w)即为minZ(w)。目标函数变为
这里b的值与w有关,可由w求出,故在写公式时没有将其写出,实际上b也是个变量。
我们将min和max的位置对换一下,就得到这个问题的对偶问题:
什么是对偶问题:
任何一个求极大化的线性规划问题都有一个求极小化的线性规划问题与之对应,反之亦然,如果我们把其中一个叫原问题,则另一个就叫做它的对偶问题,并称这一对互相联系的两个问题为一对对偶问题。
因此,上上一个目标函数就称为原问题,上一个公式称为对偶问题。
3、证明对偶问题的最优解是原始问题最优解的下界
交换之后的对偶问题与原始问题的解并不相等,但是在一定条件下,存在对偶问题与原始问题的解相等的情况。
设
则可知
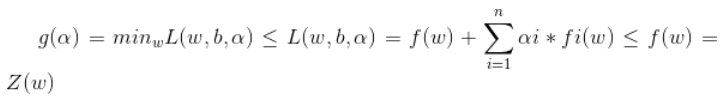
即d*<=p*。对偶问题的最优解是原始问题最优解的下界。
4、 如何令对偶问题与原问题最优解相等
d*<=p*称为弱对偶性,d *=p *称为强对偶性。若对偶问题与原始问题满足强对偶性,则求解原始问题的最优解即可转为求对偶问题的最优解。
转化为对偶问题求解的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。
4.1 Slater条件
Slater 条件是指存在严格满足约束条件的点 x ,这里的“严格”是指 fi(x)≤0 中的“小于或等于号”要严格取到“小于号”,亦即,存在 x 满足:
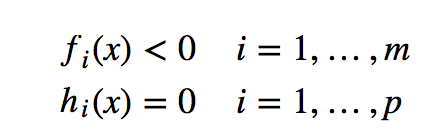
我们有:如果原始问题是凸优化问题(很庆幸,SVM的规划问题是一个凸优化问题),并且满足 Slater 条件的话,那么 strong duality 成立。需要注意的是,这里只是指出了 strong duality 成立的一种情况,而并不是唯一情况,不过研究SVM的话 ,知道这种情况足够了。
很显然,我们可以知道存在w满足fi(w)<0,即原始问题满足Slater条件且由于原始问题是凸优化问题,故强对偶性成立,即对偶问题最优解与原始问题最优解相等。
这样我们就成功把求解原始问题转为求解对偶问题。
5、 由强对偶性成立推导KKT条件
假设w*、b*和a *分别为原始问题和对偶问题的极值点,相应的极值为p *和d *,首先p *=d *,
左右两端其实是相等的,故可将小于等于号改为等号。
由第一个不等号变化,可以得到w *是L(w,b,a *)的一个极值点,由此可以知道L(w,b,a *)在x *处的梯度为0,即:
由第二个不等号变化可得:
i=1,2,3…n,此条件称为互补性条件。
互补性条件有着重要的意义。它说明了当fi(w *)<0时,x *是处于可行域的内部的,这时不等式约束并不起作用,此时ai *=0;而ai *>0的点肯定是可行域边界的点(fi(w *)=0。也就是说只有积极约束才有不为0的对偶变量。而这在支持向量机中有着重要的意义。
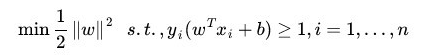
哪些不等式约束对应着不为0的对偶变量呢?显然,只有当yi(wTxi+b)=1时,这个约束对应的对偶变量才可能不为0,这意味着什么?意味着这个约束对应的样本点xi是支持向量!也就是说:
只有支持向量才对应不为0的拉格朗日乘子!
综上我们可以得到SVM情况下的KKT条件形式
任何满足强对偶性(不一定要求是通过Slater条件得到,也不一定要求是凸优化问题)的问题都满足KKT条件,换句话说,这是强对偶性的一个必要条件。不过,当原始问题是凸优化问题的时候(当然还要求一阶函数是可微的,否则KKT条件的最后一个式子就没有意义了),KKT就可以升级为充要条件。换句话说,如果原始问题是一个凸优化问题,且存在 x˜ 和 (λ˜,ν˜) 满足 KKT 条件,那么它们分别是原始问题和对偶问题 的极值点并且强对偶性成立。