机器学习 --- 支持向量机的核函数

一、核函数方法的直观理解

线性向量机地分类效果可能并不是很好，难以分类非线性的问题，这就将引入核函数。

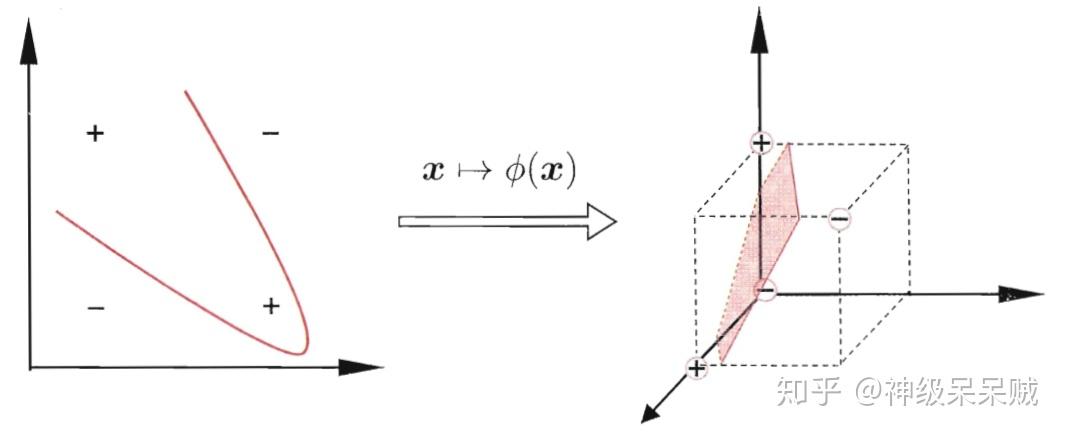
例如在二维平面中，难以通过线性的方法来处理异或问题，但是通过将输入变量经过核函数 映射到三维空间中，那么如上图所示的线性超平面可以完成分类。

在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数，将样本从原始空间映射到高维特征空间，最终在高维特征空间中构造出最优的划分超平面。

因此，在高维的特征空间划分超平面模型表示成：

 表示成经过核函数将  映射后的特征向量。

二、求解带核函数的支持向量机

由之前线性支持向量机的推导，可以得到：

由线性向量机的知识，推出带核函数的规划方程：

同样的，其对偶问题：

定义 ，(1)式重写成：

使用拉格朗日乘子法求解出  后就能得到参数 

三、核函数

如果一个对称函数所对应的核矩阵  半正定，它就能作为核函数使用。使用核函数做特征映射可能隐式地定义了特征空间，因此选取合适的核函数很重要，下面列举一些常用的核函数。

1.高斯核函数

高斯核函数可以将数据从低维映射至高维甚至无穷维。是最常用的核函数之一。

三维空间中，选取不同的  获得不同的图像

 ：

：

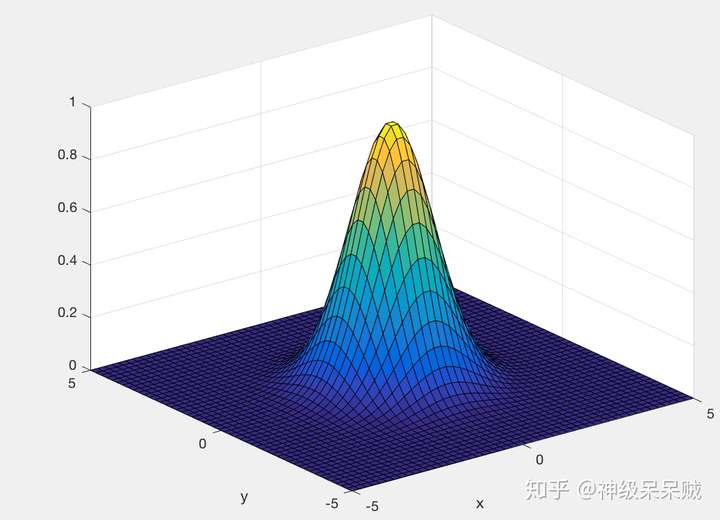
通过调节  可以获得很高的灵活性，当  选取过大，高次特征权重衰减得很快，因此就相当于一个低维子空间，可能会带来高偏差，低方差的现象，反之，高次特征权重衰减得缓慢，可将任意的数据映射为线性可分，可能会带来低偏差，高方差的现象。

2.线性核

3.多项式核

4.拉普拉斯核

5.Sigmoid核

还可以通过函数组合得到：

• 若  为核函数，对于任意的正数  ，其线性组合：  也是核函数
• 若  为核函数，函数的笛卡儿积：  也是核函数
• 若  为核函数，对于任意的函数  ，  也是核函数

参考文献：

1.支持向量机通俗导论（理解SVM的三层境界） - Mac Track - CSDN博客

2.拉格朗日对偶问题（Lagrange duality）

3.深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

4.周志华. 机器学习[M]. 清华大学出版社, 2016

5.Andrew Ng 《machine learning》系列课程