前言
支持向量机(Support Vector Machines, SVM)是一个非常出色的二类分类模型,被成功应用于很多机器学习应用中。这里的“机”实质上是指算法。要在笔记中把SVM完完全全讲清楚是非常困难的,一是因为这个东西本身很难理解,需要花很多时间和精力去深入学习和研究;二是因为其中涉及的数学原理非常多,以本人的数学水平也不能完全说得清楚,需要不断深入学习。因此只能力图把自己已经理解的东西梳理清楚。关于支持向量机的笔记分为三篇,本篇主要把SVM的数学原理描述一遍,并给出最大间隔法及核技巧的Matlab代码实现。
一、问题引入
1.线性分类器
在Logistic回归模型中,我们已经构建出了一个线性分类器,即画出一条决策边界,把两类数据分开:

其中使用的假设函数亦即sigmoid函数:
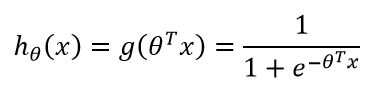
根据这个函数,当有一个新的样本加入时,我们只需要计算h_θ(x)的值,当h_θ(x)>0.5时,判断属于1类;当h_θ(x)<0.5时,判断属于0类。图中画出的决策边界并不是十分理想,很多情况下,我们往往希望决策边界与两边的样本点的距离都尽可能大一些,这样我们作出的决策会更加准确。亦即,当θTx>>0时,h_θ(x)=1;当θTx<<0时,h_θ(x)=0。现在我们把问题转化一下,逐渐过渡到支持向量机。

我们把θ0替换成b,表示截距。把剩下的项的θ替换成w,得:
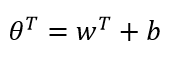
假设函数变为:
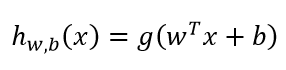
输出y为0,1变为-1,+1,这种转化之后便于使用符号函数表示。于是问题转化为:给定线性可分训练数据集,通过间隔最大化求解相应的凸二次规划问题得到决策超平面为:
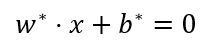
以及分类决策函数:

我们就得到了最简单的线性可分支持向量机。
二、问题分析
1.函数间隔和几何间隔
由于支持向量机的学习策略是间隔最大化,因此在介绍算法之前,先交待清楚函数间隔和几何间隔的概念。
1.1 函数间隔
对于给定的训练数据集T和超平面(w, b),定义超平面(w, b)关于样本点(xi, yi)的函数间隔为:
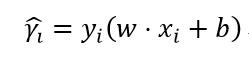
函数间隔可以表示分类预测的确信度。但是当我们成比例地改变w和b时,超平面没有改变,函数间隔却成比例改变了。所以我们要对法向量w加以约束,例如取单位法向量。
1.2 几何间隔
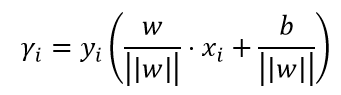
几何间隔是规范化的函数间隔,即当||w||=1时,函数间隔等于几何间隔。函数间隔与几何间隔的关系如下:
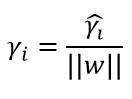
2.最大间隔法
最大间隔法的直观解释是:对训练数据进行分类时,找到几何间隔最大的超平面,使之分为正负两类。几何间隔最大意味着决策置信度最大。
2.1 硬间隔最大化
硬间隔最大化主要针对线性可分支持向量机。这个问题可描述为:
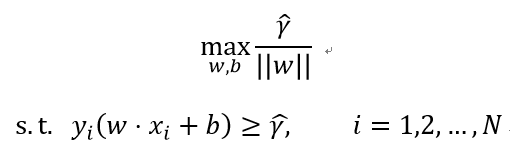
函数间隔的取值并不影响最优化问题的解,可以取γ=1.于是问题可改写为:
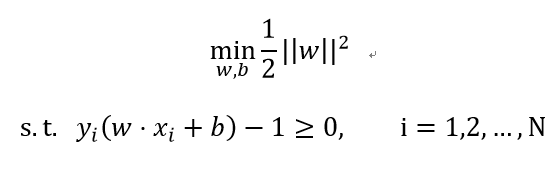
这是一个凸二次规划(convex quadratic programming)问题。根据这个问题求得最优解w*, b*,由此得到决策分类超平面:
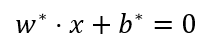
以及分类决策函数:
距离分类决策超平面最近的样本点的集合称为支持向量。
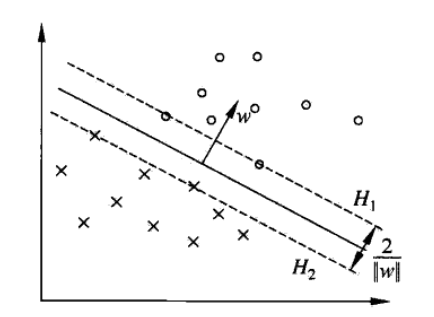
如图中H1,H2上的点就是支持向量。之所以叫这个名字,是因为这些点定义或者支持这个决策边界。
2.2 原始问题与对偶问题
以上问题作为原始最优化问题。很多时候,求解原始问题(primal problem)的对偶问题(dual problem)往往更加容易。下面介绍原始问题和对偶问题的概念。
考虑约束最优化问题:
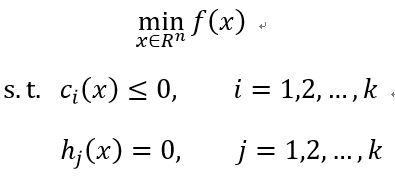
称此问题为原始最优化问题。
定义广义拉格朗日函数:
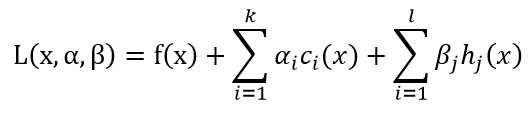
这里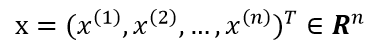
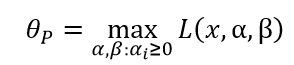
这里P表示原始问题。有如下结论:

此时我们可以认为θP函数是把目标函数和约束函数结合在一起的问题。对上式取极小值:
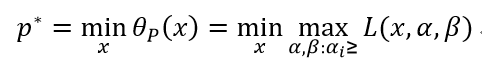
称p*为原始问题取得最优解时的函数值。
定义:
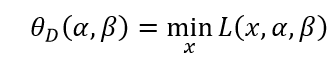
其中D表示对偶问题。再取其极大值:
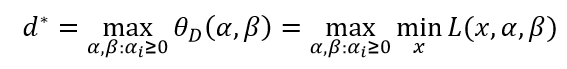
称此问题为原始问题的对偶问题,其中d*为对偶问题的最优值。一般情况下,对偶问题和原始问题的值满足:d*≤p*。等号成立时,满足KKT(Karush-Kuhn-Tucker)条件:
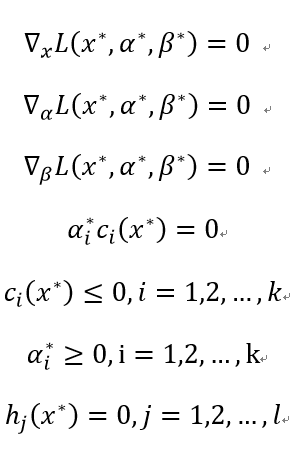
2.3 最大间隔分类器的对偶问题
由2.1中的原问题,该问题对应的拉格朗日方程为:
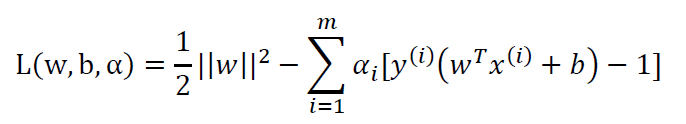
分别对w,b求偏导数并令其等于0:
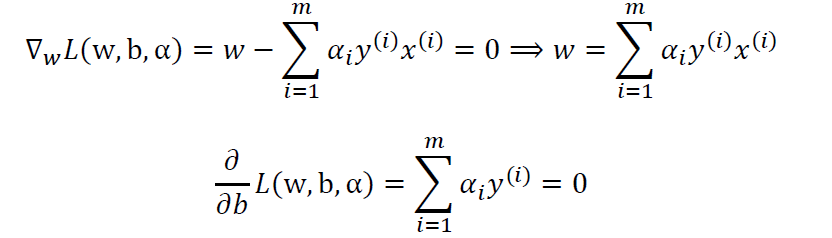
将结果回代L(w,b,α):
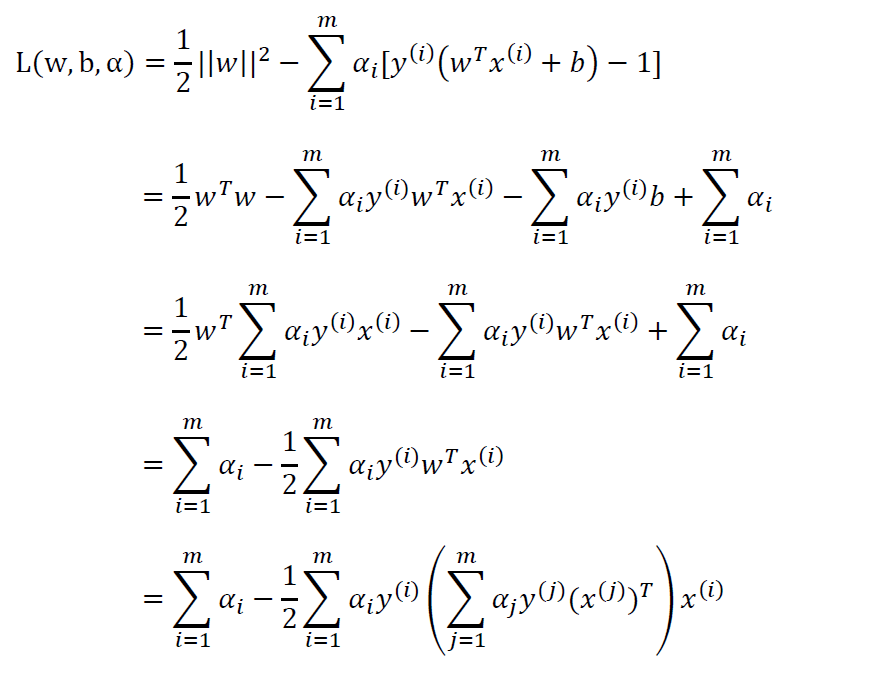

最终,我们得到原始问题的对偶问题:
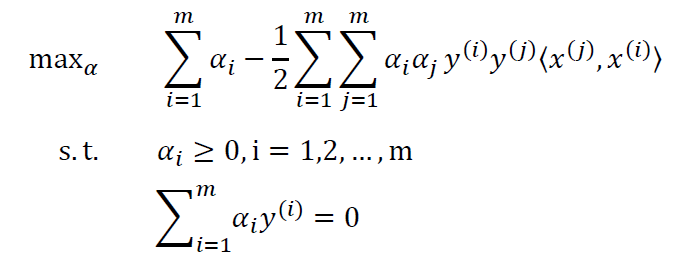
其中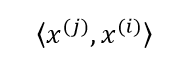
2.4 软间隔最大化
之前的线性分类器一直强调硬间隔,是指训练数据是线性可分的。但是对线性不可分的训练数据并不适用。线性不可分意味着某些样本点(xi, yi)不能满足函数间隔大于等于1的约束条件,为了解决这个问题,我们修改一下约束条件:
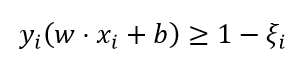
目标函数变成:
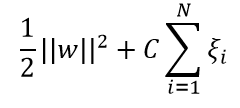
线性不可分的线性支持向量机的学习问题如下:
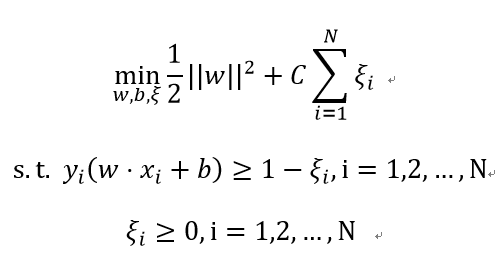
同样地求其对偶问题:
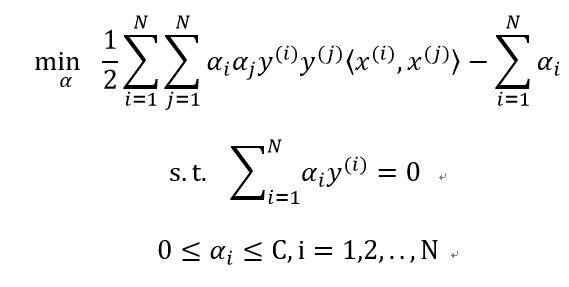
求得分类超平面:
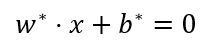
其中:
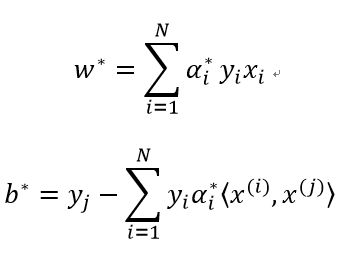
2.5 核技巧
核技巧往往用于非线性分类器。在非线性分类器中,决策边界一般是曲平面或者封闭的曲平面。非线性问题往往不容易求解,所以希望能将它转化为线性分类器求解。所采取的方法时进行一个非线性变换,将非线性问题变换为线性问题。
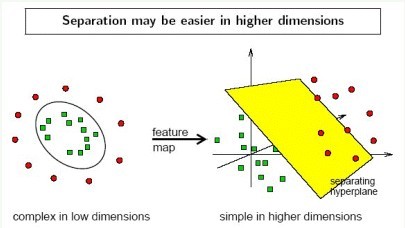
核技巧便是能解决这种问题的方法:首先使用一个变换把原空间的训练数据映射到新空间(一般是高维度或无限维空间),使数据线性可分的概率增大,然后在新空间里用线性分类器从训练数据中学习分类模型。但是,当数据映射到高维度空间后,算法的时间复杂度会大大增加,因此需要引入核函数。核函数的作用在于,引入核函数不需再显式地定义出映射函数,就能计算两个高维空间中的向量的内积,而且时间复杂度降低。SVM中广泛使用高斯核:
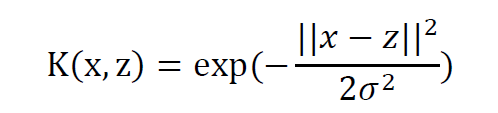
一个合法的核函数必定能写成两个映射函数相乘的形式。为了分析核函数是否合法,定义一个核矩阵K:
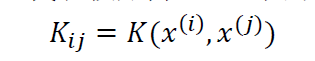
由定义显然可知Kij=Kji,K是一个对称矩阵。对于任意的m维向量z,有:
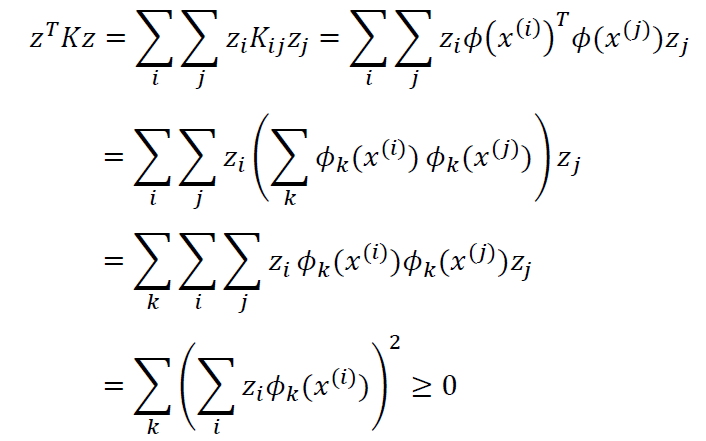
K是对称半正定矩阵。因此,核函数K合法的充分必要条件是对应核矩阵K是对称半正定矩阵。
核函数并不只是应用于SVM的,只要算法中出现了内积的计算,都可以考虑使用核函数,从而提高处理高维数据的性能。
三、Matlab代码实现
1.硬间隔支持向量机
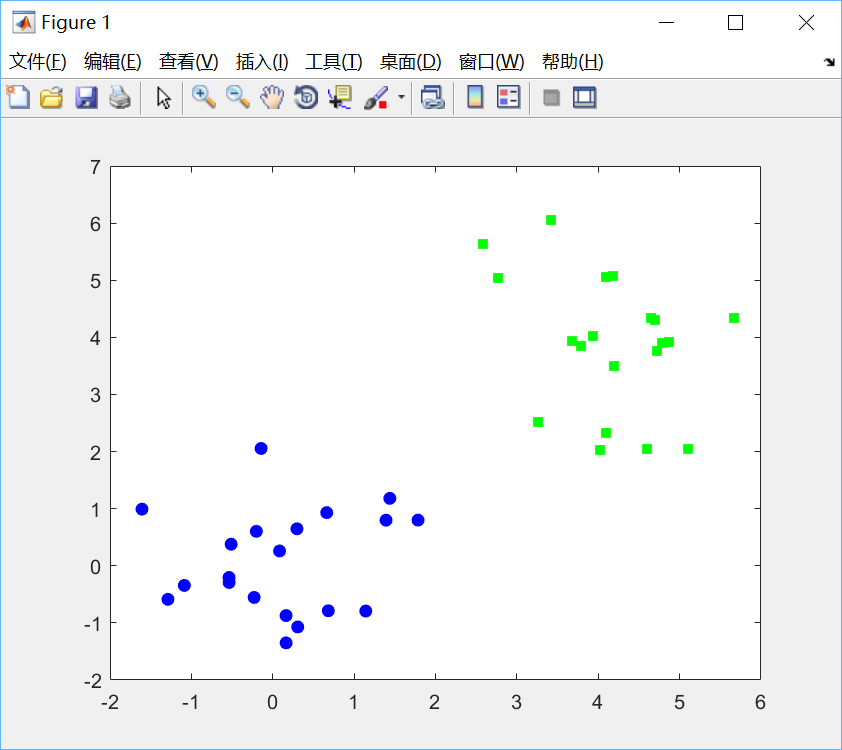
(1)生成数据并绘图:
%% 随机生成数据
x = [randn(20,2);randn(20,2)+4];
y = [repmat(-1,20,1);repmat(1,20,1)];
%% 绘制散点图
ma = {'bo','gs'};
fc = {[0 0 1],[0 1 0]};
yv = unique(y);
figure(1); hold off
for i = 1:length(yv)
pos = find(y==yv(i));
plot(x(pos,1),x(pos,2),ma{i}, 'markerfacecolor',fc{i});
hold on
end绘制效果如下:
(2)求解二次规划问题:
%% 设置二次规划问题中的参数及输入数据
N = size(x,1);
K = x*x';
H = (y*y').*K + 1e-5*eye(N);
f = repmat(1,N,1);
A = [];b = [];
LB = repmat(0,N,1); UB = repmat(inf,N,1);
Aeq = y';beq = 0;
% runs the SVM
alpha = quadprog(H,-f,A,b,Aeq,beq,LB,UB);
% 计算偏差
fout = sum(repmat(alpha.*y,1,N).*K,1)';
pos = find(alpha>1e-6);
bias = mean(y(pos)-fout(pos));算法调用了Matlab的二次规划函数quadprog,具体说明可自行查询。
(3)画出决策边界:
figure(1);hold off
% 绘制支持向量
pos = find(alpha>1e-6);
plot(x(pos,1),x(pos,2),'ko','markersize',15,'markerfacecolor',[0.6 0.6 0.6],...
'markeredgecolor',[0.6 0.6 0.6]);
hold on
for i = 1:length(yv)
pos = find(y==yv(i));
plot(x(pos,1),x(pos,2),ma{i},'markerfacecolor',fc{i});
end
xp = xlim;
% 画出线性分类器的决策边界
w = sum(repmat(alpha.*y,1,2).*x,1)';
yp = -(bias + w(1)*xp)/w(2);
plot(xp,yp,'r','linewidth',2)运行效果如下:
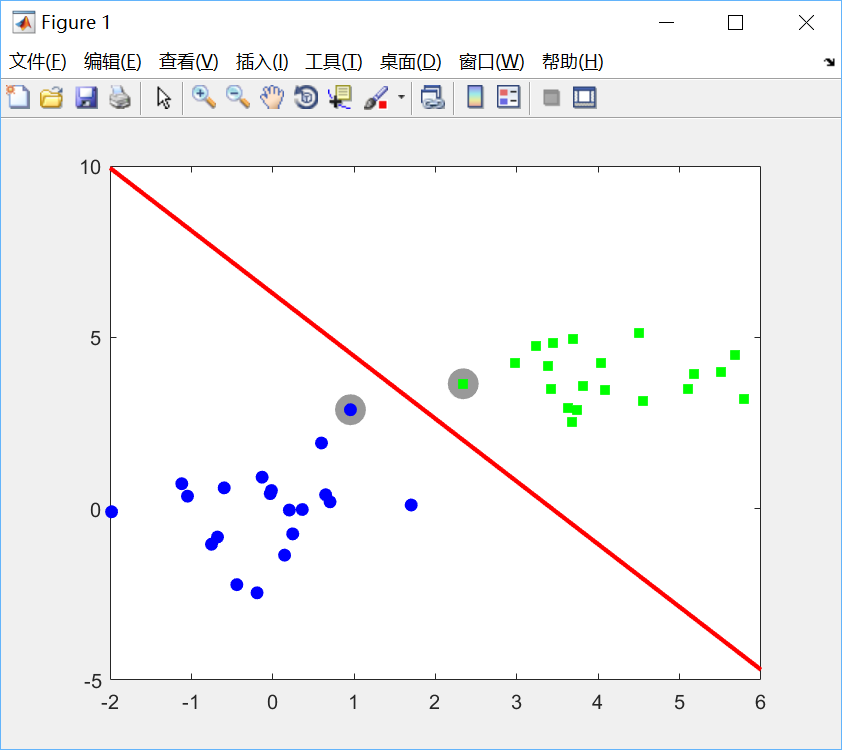
图中灰色标注的样本点便是支持向量。
2.软间隔支持向量机
(1)随机生成数据并绘图:
%% 随机生成数据
x = [randn(20,2);randn(20,2)+4];
y = [repmat(-1,20,1);repmat(1,20,1)];
% 添加错误离群点
x = [x;2 1];
y = [y;1];
%% 绘制数据
ma = {'bo','gs'};
fc = {[0 0 1],[0 1 0]};
yv = unique(y);
figure(1); hold off
for i = 1:length(yv)
pos = find(y==yv(i));
plot(x(pos,1),x(pos,2),ma{i},'markerfacecolor',fc{i});
hold on
end
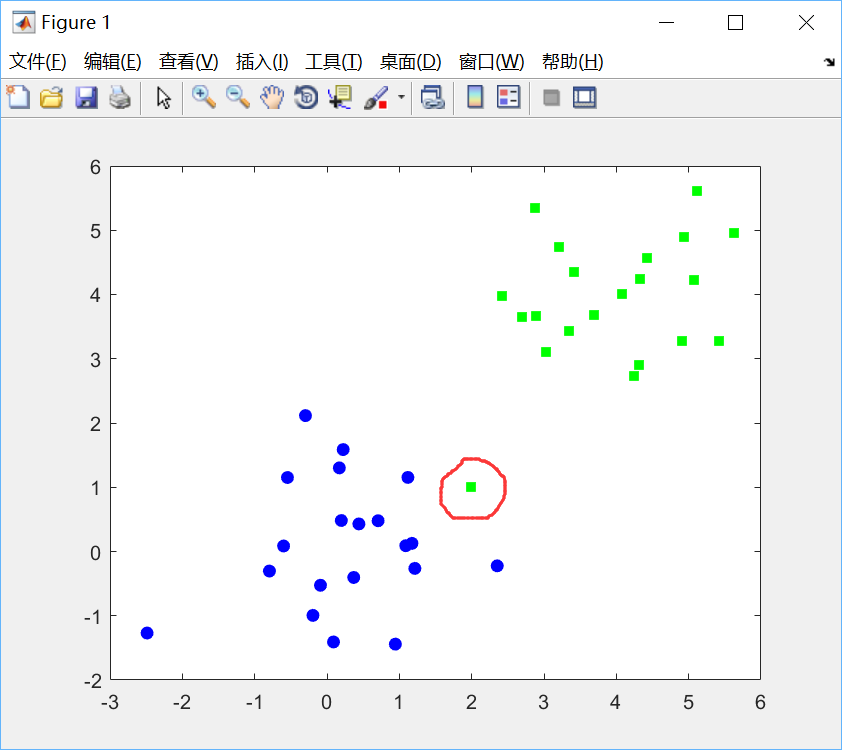
可见有一个绿点离群。
(2)求解二次规划问题:
此处与硬间隔唯一不同的地方就是α的约束上界C,这个参数需要不断调整。
%% 设置二次规划问题的参数
N = size(x,1);
K = x*x';
H = (y*y').*K + 1e-5*eye(N);
f = repmat(1,N,1);
A = [];b = [];
LB = repmat(0,N,1); UB = repmat(inf,N,1);
Aeq = y';beq = 0;
C = 0.01;
UB = repmat(C,N,1);
% runs the SVM
alpha = quadprog(H,-f,A,b,Aeq,beq,LB,UB);
% 计算偏差
fout = sum(repmat(alpha.*y,1,N).*K,1)';
pos = find(alpha>1e-6);
bias = mean(y(pos)-fout(pos));(3)画出决策边界:
figure(1);hold off
pos = find(alpha>1e-6);
plot(x(pos,1),x(pos,2),'ko','markersize',15,'markerfacecolor',[0.6 0.6 0.6],...
'markeredgecolor',[0.6 0.6 0.6]);
hold on
for i = 1:length(yv)
pos = find(y==yv(i));
plot(x(pos,1),x(pos,2),ma{i},'markerfacecolor',fc{i});
end
xp = xlim;
yl = ylim;
% 画出决策边界.
w = sum(repmat(alpha.*y,1,2).*x,1)';
yp = -(bias + w(1)*xp)/w(2);
plot(xp,yp,'r','linewidth',2);
ylim(yl);
ti = sprintf('C: %g',C);
title(ti);
分别设置C=1,C=0.01绘图如下:
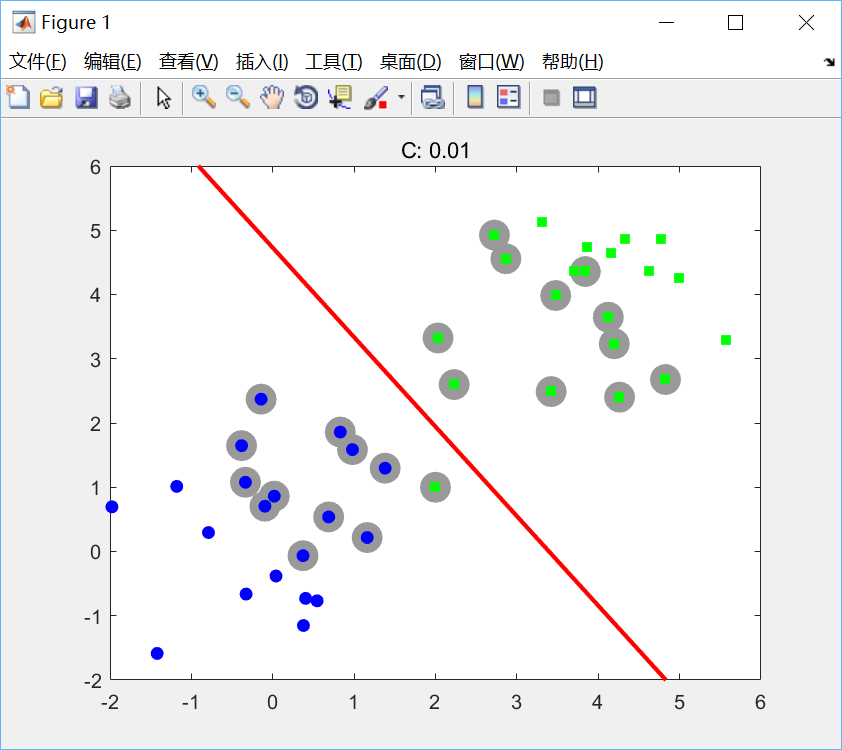
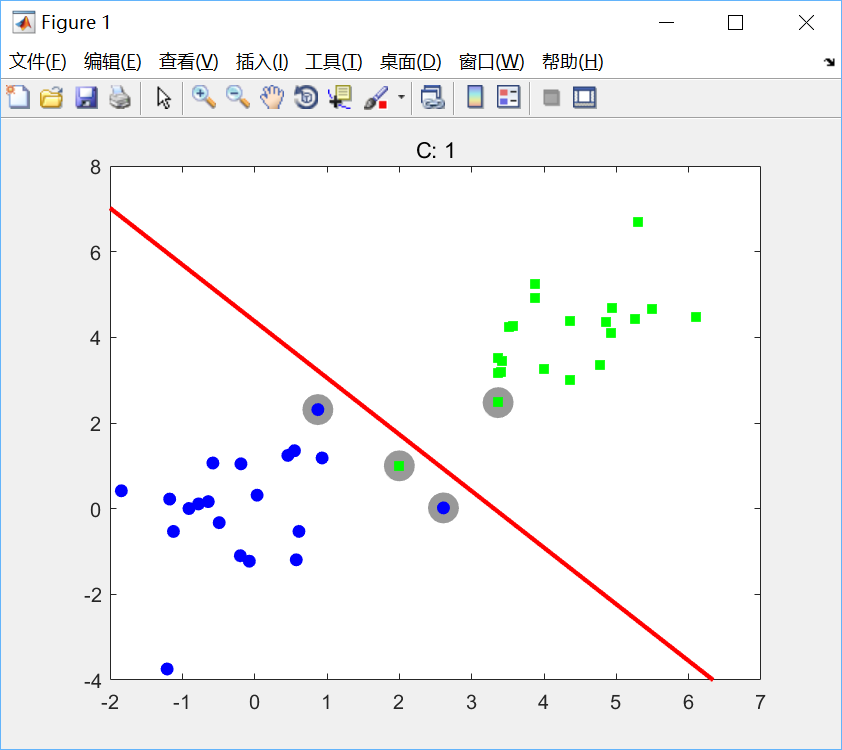
可见,软间隔允许训练点落在分类错误的一边。随着C的增大,每个训练点对最大值的影响被削弱。
3.非线性支持向量机(使用高斯核)
(1)导入数据并绘图:
%% 导入数据
load('SVMdata2')
[t I] = sort(t);
X = X(I,:);
%% 绘制散点图
ma = {'bo','gs'};
fc = {[0 0 1],[0 1 0]};
tv = unique(t);
figure(1); hold off
for i = 1:length(tv)
pos = find(t==tv(i));
plot(X(pos,1),X(pos,2),ma{i},'markerfacecolor',fc{i});
hold on
end
绘制效果如下:
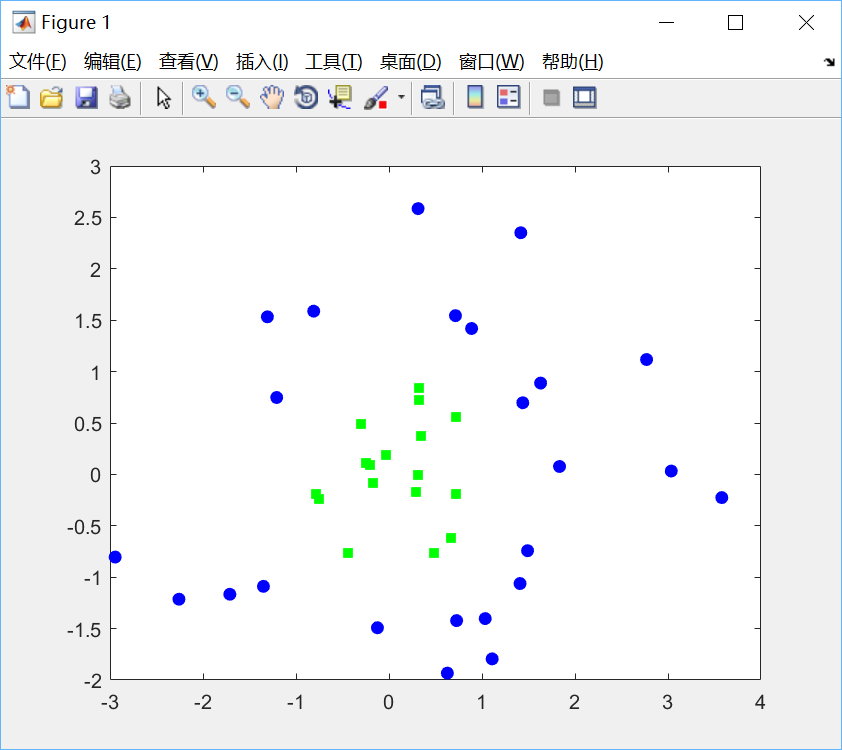
(2)计算高斯核函数并求解二次规划:
[Xv Yv] = meshgrid(-3:0.1:3,-3:0.1:3);
testX = [Xv(:) Yv(:)];
N = size(X,1);
Nt = size(testX,1);
K = zeros(N);
testK = zeros(N,Nt);
% 设置高斯核函数的参数
gam = 10;
for n = 1:N
for n2 = 1:N
K(n,n2) = exp(-gam*sum((X(n,:)-X(n2,:)).^2));
end
for n2 = 1:Nt
testK(n,n2) = exp(-gam*sum((X(n,:)-testX(n2,:)).^2));
end
end
% 设置二次规划函数的参数
H = (t*t').*K + 1e-5*eye(N);
f = repmat(1,N,1);
A = [];b = [];
LB = repmat(0,N,1); UB = repmat(inf,N,1);
Aeq = t';beq = 0;
C = 10;
UB = repmat(C,N,1);
% Following line runs the SVM
alpha = quadprog(H,-f,A,b,Aeq,beq,LB,UB);
fout = sum(repmat(alpha.*t,1,N).*K,1)';
pos = find(alpha>1e-6);
bias = mean(t(pos)-fout(pos));
% 计算预测值
testpred = (alpha.*t)'*testK + bias;
testpred = testpred';(3)绘制决策边界:
for i = 1:length(tv)
pos = find(t==tv(i));
plot(X(pos,1),X(pos,2),ma{i},'markerfacecolor',fc{i});
end
contour(Xv,Yv,reshape(testpred,size(Xv)),[0 0],'r','LineWidth',2);
ti = sprintf('Gamma: %g',gam);
title(ti);分别取(C, γ)为(10, 1),(10, 10),(10, 50)绘图如下:
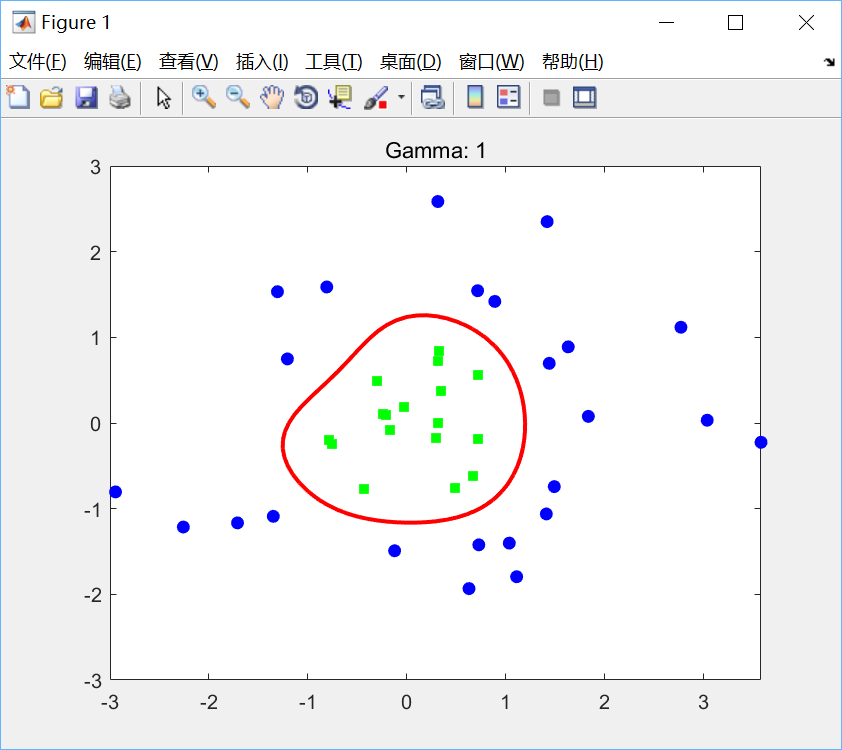
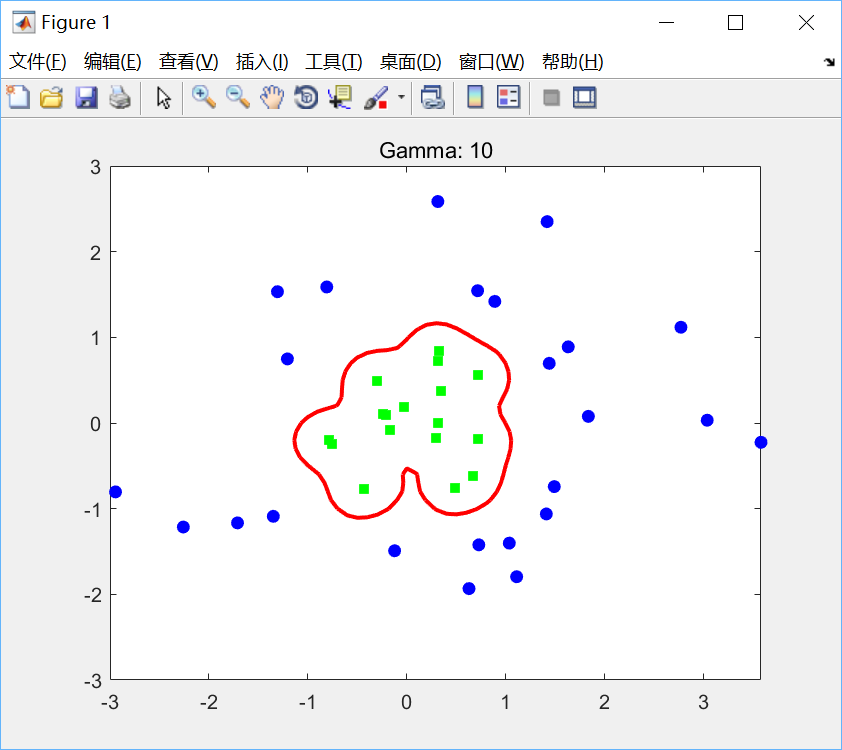
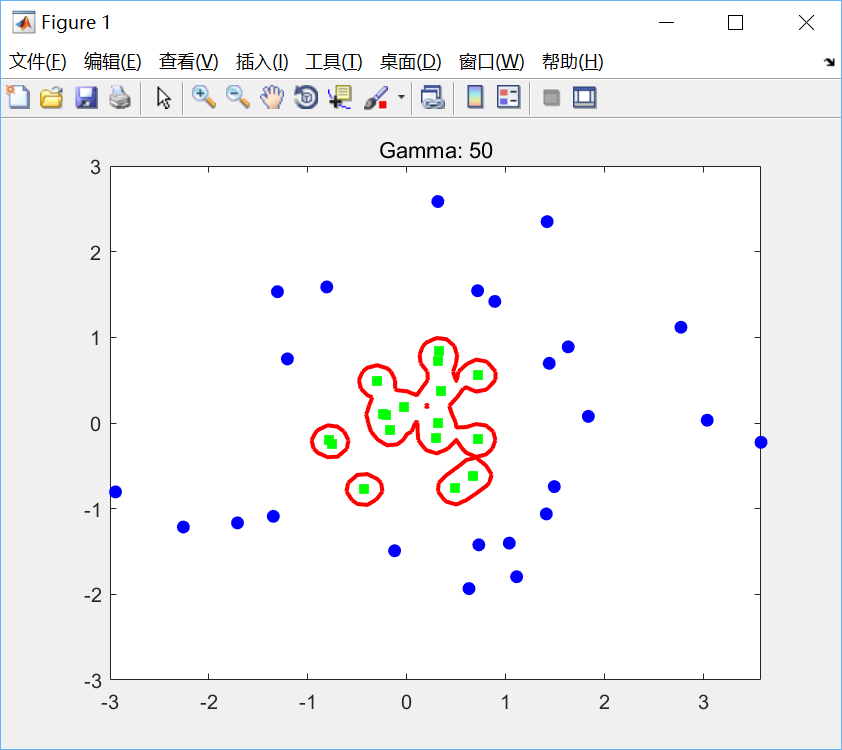
可见,在高斯核中增加γ会增加原始空间中决策边界的复杂性。γ选得越小,意味着高斯函数的方差越大,高斯函数衰减越快,映射到高维空间中的高次特征权重会很小,此时相当于映射到一个维度并不比原空间高很多的空间,因此线性可分程度弱一些;反之,γ选得越大,意味着高斯函数的方差越小,高次特征权重会很大,此时就会映射到一个维度比原来高很多的空间,线性可分程度很高,甚至每个样本点都是线性可分的,出现严重的过拟合问题。
