目录
一、什么叫做线性赋范空间
1. 距离:
2. 线性空间:
- 有向量的加法和数乘
- 满足:
向量加法结合律:u + (v + w) = (u + v) + w;
向量加法交换律:v + w = w + v;
向量加法的单位元:V 里有一个叫做零向量的 0,∀ v ∈ V , v + 0 = v;
向量加法的逆元素:∀v∈V, ∃w∈V,使得 v + w = 0;
标量乘法分配于向量加法上:a(v + w) = a v + a w;
标量乘法分配于域加法上: (a + b)v = a v + b v;
标量乘法一致于标量的域乘法: a(b v) = (ab)v;
标量乘法有单位元: 1 v = v, 这里 1 是指域 F 的乘法单位元。
3. 定义范数

赋予范数或者距离的几何分别称为:赋范空间和度量空间;
若在其上再加上线性结构称为线性赋范空间和线性度量空间。
二、图的定义
图(Graph)是由顶点的有穷非空集合和顶点之间的集合组成,通常表示为:G(V, E),其中 G 表示一个图,V 是图 G 中顶点的集合,E 是图 G 中边的集合。
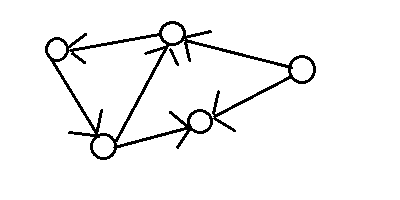
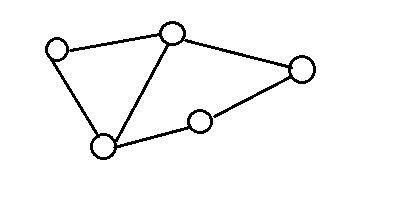
图的表示:一般使用圆圈表示顶点,使用线段表示边,一条边连接两个不同的顶点。有些边是带方向的称为有向边,当顶点v到u含有一条有向边,就画一个箭头从v指向u,使用元组(v,u)表示;而没有方向的边称为无向边,当顶点v到u含有一条有向边,就画一条线段从v指向u,使用元组(v,u)表示。例如下面分别是有向图和无向图。
有向图 无向图
图根据边的分类分为有向图和无向图,有向图的边是有向边,它就像公路的单行道一样,只能从一个方向到另一个方向。无向图的边是无向边,当然它就像双向车道一样可以互相到达,而且两个顶点是没有区别的。
当且仅当(u,v)是图的边,称顶点v和u是邻接的。边(u,v)关联于顶点u和v。对于无向图这种邻接和关联是对等的,而有向图是单向的,它仅仅从u到v。
权:在图的一些应用中,可能要为每条边赋予一个表示大小的值,这个值就称为权。例如从城市A到城市B存在一条公路,而可以使用权表示这条公路的距离。
路径:一个顶点序列i1,i2........ik是图的一条路径,当且仅当边(i1,i2)(i2,i3).........(ik-1,ik)都在图中。如果除了第一个顶点和最后一个顶点之外,其余的顶点均不相同,那么这条路径称为简单路径。
连通图:设图G是无向图,当且仅当G的每一对顶点之间都有一条路径,则称G是连通图。
子图:如果图H的顶点和边的集合是图G的子集,那么称图H是图G的子图。
生成树:如果图H是图G的子图,且他们的顶点集合相同,并且H是没有环路的无向连通图(即一棵树),则称H是G的一棵生成树。
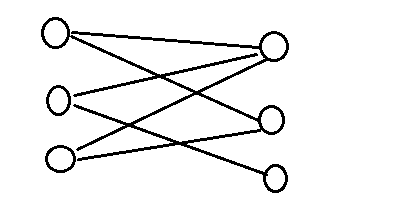
二分图:图G的顶点被分为两个子集,而且每条边只能从一个子集到另一个子集。例如:
强连通图:图G是一个有向图,当且仅当每一对不同的顶点u,v,从u到v和v到u都有一条有向路径。
三、激活函数
1. 笔记
sigmoid [维基百科]
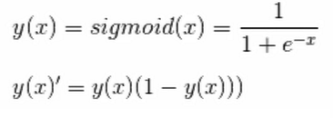
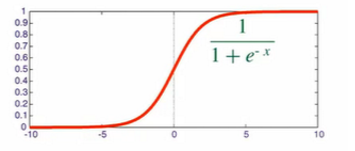
tanh [维基百科]

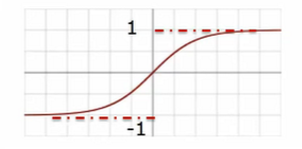
ReLU [维基百科]

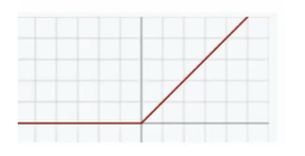
正向截断负值,损失大量特征(特征足够多,所以即使截断80%后还能用)
反向梯度没有损失
Leaky ReLU [维基百科]

更加有效率的梯度下降以及反向传播:避免了梯度爆炸和梯度消失问题。
简化计算过程:没有了其他复杂激活函数中诸如指数函数的影响;同时活跃度的分散性使得神经网络整体计算成本下降。
2. 维基百科
这里我贴上了维基百科上关于激活函数的各种类型的介绍,如下所示:



3. Feisky
四、R^n的紧致子集
设(X, ρ)是一个度量空间,A ∈ X,如果存在实数M>0使得ρ(x, y)<M对于所有的x, y∈A成立,则称A是X的一个有界子集;如果X本身是一个有界子集,则称度量空间(X, ρ)是一个 有界度量空间。
紧致度量空间是有界的。
度量空间的每个紧致子集都是有界子集
一个直观一点的理解,几个集合是“紧”的,就是说,无限个点撒进去,不可能充分散开。无论邻域多么小,必然有一些邻域里面有无限个点。上面关于 compactness的这个定义的玄机就在有限和无限的转换中。一个紧的集合,被无限多的小邻域覆盖着,但是,总能找到其中的有限个就能盖全。那么,后果是什么呢?无限个点撒进去,总有一个邻域包着无数个点。邻域们再怎么小都是这样——这就保证了无限序列中存在极限点。
五、《无限逼近理论》阅读
维基百科:Universal approximation theorem
六、x1 ~ x6,n1 ~ n9,y1 ~ y4,写输出公式