1、拟合程度

对于线性回归：
对于逻辑回归：

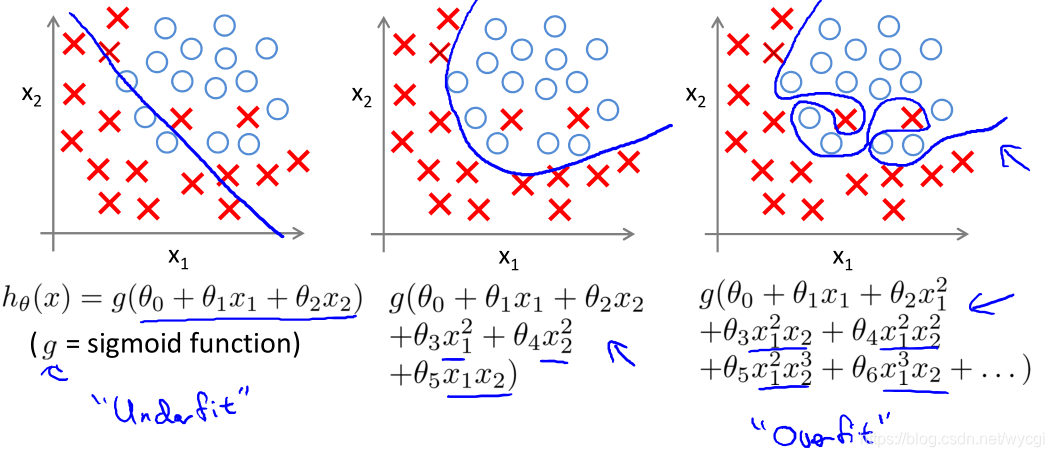
左图欠拟合，高偏差。中图正合适。右图过拟合，高方差。

1.1、过拟合

1.1.1、原因

由上面的右图可知，特征太多（线性回归中四个特征： $x$ 、 $x^2$ 、 $x^3$ 、 $x^4$ ；逻辑回归中特征更多，不赘述），虽然能够贴合训练集中的样本，但是无法“泛化”（也即无法将模型应用到新的样本中）。
样本数量不够

1.1.2、理论解决方法

减少特征数量：手动选取特征或者采用模型选择算法（之后的博文会提到）。
减小模型参数 $\theta$ ，如：正则化

1.1.3、实际解决方法之一：正则化

主要思想：减小模型参数 $\theta$
具体操作：在代价函数中添加惩罚项
如果假设函数如下所示：
$h_\theta(x)=\theta_0+\theta_1x+\theta_2x^2+\cdots+\theta_4x^4$
则代价函数可添加惩罚项 $1000\theta_3^2$ 和 $1000\theta_4^2$ ：
$J(\overrightarrow{\theta})=\frac{1}{2m}[\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))^2 + 1000\theta_3^2+1000\theta_4^2]$
这样，在求目标函数（使代价函数最小）时，会要求 $\theta_3$ 和 $\theta_4$ 的值变小，因为这两个值对代价函数的值有一定影响，一定程度上弱化了与这两个模型参数对应的特征（ $x^2$ 和 $x^3$ ）在假设函数中的作用。

1.1.3.1、正则化线性回归

惩罚项为： $\lambda\sum_{j=1}^n\theta_j^2$ ，其中， $\lambda$ 为正规化参数，如果设置过大，则各模型参数过于接近零（除了 $\theta_0$ ），相当于假设函数 $h_\theta(x)=\theta_0$ 。

PS: 注意惩罚项的累加符号是从 $j=1$ 开始的，也就是说从 $\theta_1$ 开始，对 $\theta_0$ 没有影响，因为 $\theta_0$ 并没有对应的特征 $x$ 。

代价函数如下：
$J(\overrightarrow{\theta})=\frac{1}{2m}[\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))^2 + \lambda\sum_{j=1}^n\theta_j^2]$
梯度下降中的偏导数如下：
$\theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))(x^{(i)}_0) \\ \theta_j:=\theta_j-\alpha[\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))(x^{(i)}_j)+\frac{\lambda}{m}\theta_j] \quad (for\quad j = 1至n)$
PS： $x^{(i)}_0=1；j为0至n$

上面第二条公式可以化为：
$\theta_j:=\theta_j(1-\frac{\lambda}{m})-\frac{\alpha}{m}\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))(x^{(i)}_j) \quad (for\quad j = 1至n)$
由 $1-\frac{\lambda}{m}\lt1$ 可知，相比原来的代价函数减小了 $\theta_j$ 的值。
$1-\frac{\lambda}{m}\lt1$ 的原理为：因为 $\lambda$ 不可能是负数，
如果是负数，则 $\lambda\sum_{j=1}^n\theta_j^2$ 这个项也是负数，在求解目标函数时可以取无穷大的模型参数，使代价函数无穷小，进而不存在真正的最小值，不合理。

1.1.3.2、正则化正规方程法

原式子：
$\theta = (X^TX)^{-1}X^Ty$
正则化后的式子：
$\theta = (X^TX \begin{bmatrix} 0 & 0 & \dots & 0 \\ 0 & 1 & 0 & \vdots \\ \vdots & 0 & 1 & 0 \\ 0 & \dots & 0 & 1 \end{bmatrix} )^{-1}X^Ty$
PS：该式可以解决 $X^TX$ 不可逆的问题，新添加的矩阵大小为(n+1)*(n+1)

1.1.3.3、正则化逻辑回归

惩罚项：与线性回归相同
代价函数如下：
$J(\theta) = -\frac{1}{m} \sum_{i=1}^m [y^{(i)}\log(h_\theta(x^{(i)}) +(1-y^{(i)})\log(1-h_\theta(x^{(i)})) ] + \frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2$
-梯度下降的偏导数与线性回归中的一样。

机器学习第三周（下）

拟合