1.Kernel Trick
由上次课我们可以知道,对偶问题在求解系数q的时候仍然会被z的d所限制,虽然对偶问题表面上不受数据维度的影响,但是实际上仍然会受到限制。
这一次课我们将讲解怎么破除这种限制。
首先我们将z看作是φ对x做了变换后得到的数据。

然后我们假设φ是2nd order polynomial transform,我们将直接对x进行转换然后求内积,过程如下所示:
我们发现z的内积计算能够转换成x的内积计算然后再进行简单的组合运算。这样原本d^2的复杂度被降低为d的复杂度。

这时我们的二次规划的系数q的里面的z的内积以及求解b的z都可以用核函数代替。从而大大降低了计算的复杂度。

运用核函数的SVM计算步骤如下所示:
2.Polynomial Kernel
我们之前只推导了二次多项式的kernel,这里我们将介绍更多多项式的Kernel。
首先如果我们对二次多项式转换的一次项上添加系数
,二次项上添加
那么我们的Kernel函数就能直接转换成某个简单多项式的平方,这样使得Kernel变得更加的简单,并且添加系数不会影响转换空间z的复杂度。我们一般称添加系数后的的核函数为
。

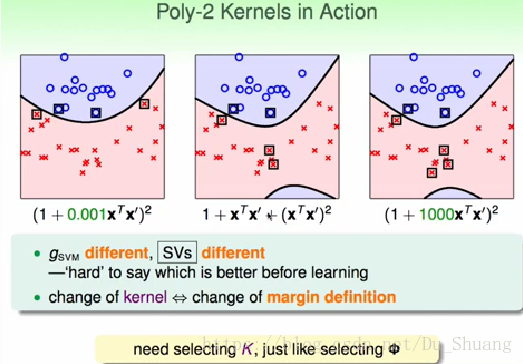
虽说添加系数后我们的转换维度不会发生变化,但是系数会影响边界距离的判定,所以添加不同的系数我们的最终求解结果也会有一定的改变,所以我们在选择Kernel时,不只要选择转换后的复杂度,还得选择系数的大小。
如果我们将二次多项式Kernel的常数项变成变量,并且将次数2变为变量Q,那么我们就得到了高次的多项式kernel.
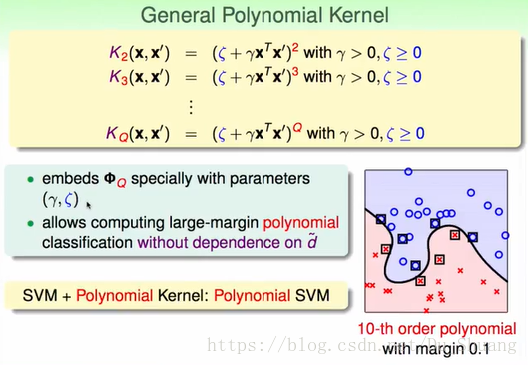
当Q=1,常数项为0时,我们就相当于对原始空间的x进行SVM求解,这时的假设空间复杂度是最低的。我们称该核为线型核。
我们建议求解的核数应该从1慢慢的往上增加,且遵循奥卡姆剃刀原则。
3.Gaussian Kernel
我们发现将
拆解然后对交叉项进行高斯展开,将变成两个无限维的向量的内积,这样我们就获得了无限维转换函数的kernel了。我们可以在kernel里面加入系数γ对结果进行微调

无限维转换是Gaussian kernel的一个解释,如果只看结果我们发现另一个解释,Gaussian Kernel只是将以SV(support vector)为中心的点gaussian函数做了一个线型组合,组合系数为α。

Gaussian Kernel的好处如下所示:
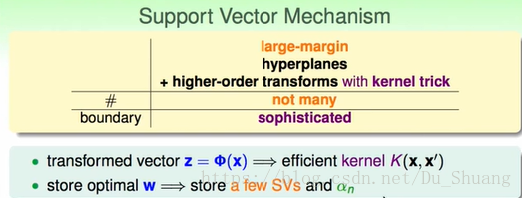

但是我们发现当γ不同时Gaussian Kernrl的结果会有很大的不同。
当γ越大,越容易overfit,因为伽马代表了Gaussian函数的宽度,γ越大,函数越廋,那么就只能区分中心点了。

所以我们要也要控制γ的大小。
4.Comparison of Kernels
这一节我们将对之前讲的三种kernel进行分析。
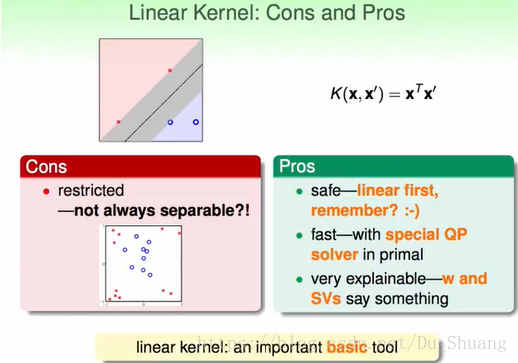
线型核:
好处:不容易过拟合,速度快,结果容易理解。
坏处:不是总能够将数据分开。
多项式核:
好处:限制少,总能够将数据分开;能主动控制Q。
坏处:计算比之前的复杂,并且计算结果的范围很大,当内部结果小于1,Q次方后接近0,大于1,Q次方后接近无穷大。并且有三个参数要进行选择,极难调试。
所以建议当Q较小时使用。
Gaussian 核:
好处:无限多维转换,能力比多项式更强,并且核函数计算更加简单,只有一个参数需要调试。
坏处:无限多维的转换,我们无法计算出无限多维的w,所以难以说明其意义。速度比线型核要低。且容易overfit。
难道我们只能用上述三个kernel吗?当然不是,我们还能自己构造出很多核函数出来,只要这些核函数满足一定的条件。
我们知道核函数是求内积,所以其具有相似型。利用其相似性我们发现用φ(x)构造的如下矩阵为半正定矩阵为其必要条件,然后数学家又证明其也是充分条件。