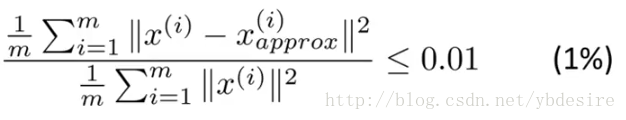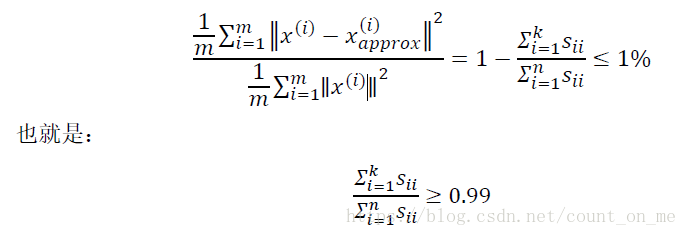主成分分析(principal component analysis)也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标(即主成分),其中每个主成分都能够反映原始变量的大部分信息,且所含信息互不重复。
PCA主要思想
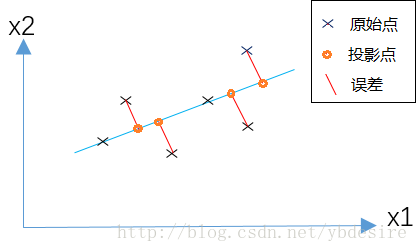
PCA的基本原理就是将一个矩阵中的样本数据投影到一个新的空间中去。当把所有的数据 都投射到该新空间时,我们希望平均方误差能尽可地小。
PCA主要步骤
-
将原始数据按行排列组成矩阵X
-
对X进行数据均值化得到X'
-
求X'的协方差矩阵C
-
求协方差矩阵C的特征值和特征向量,并将特征向量按特征值由大到小排列,取前k个按行组成矩阵P(原因:对于一个矩阵来说,将其对角化即产生特征根及特征向量的过程,也是将其在标准正交基上投影的过程,而特征值对应的即为该特征向量方向上的投影长度,因此该方向上携带的原有数据的信息越多。)
-
通过计算Y = PX',得到降维后数据Y
PCA实例 m=5
![]()
(2)、对X进行数据均值化得到X'
X'=[-2,-1,0,1,2;-2,0,-1,2,1];
(3)、求X'的协方差矩阵C
(4)、利用线性代数知识或是MATLAB中eig函数可以得到C的特征值和特征向量
![]()
![]()
对应的特征向量分别是:
![]()
![]()
因为需要将原数据降为一维,因此选择排列第一最大的特征值对应的特征向量P:
![]()
(5)、通过计算Y = PX',得到降维后数据Y
Y=PX'=[-2.82842712474619 -0.707106781186548 -0.707106781186548 2.12132034355964 2.12132034355964]
Matlab实现
MATLAB中自带了进行主成分分析的函数pca
X = [1 2 3 4 5;1 3 2 5 4];
X=X-3;%3为每一行的均值
[coeff,~,latent] = pca(X');%coeff为均值化矩阵X所对应的协方差矩阵的特征值向量,latent为均值化矩阵X所对应的协方差矩阵的特征值
[~,i] = max(latent);%求最大的特征值
P = coeff(:,i); %选取最大特征值所对应的特征向量
Y = P'*X; %y为降维后的数据,这里所乘的X为均值化后的矩阵PCA主成分数量(降维维度)选择
我们一般用PCA把n维的数据降到k维(k < n),那么k取值多少才合适呢?
PCA的原理是,为了将数据从n维降低到k维,需要找到k个向量,用于投影原始数据,是投影误差(投影距离)最小。
用公式来表示,如下
其中m表示每一个特征值的数量,即训练集中的点数。分子表示原始点与投影点之间的距离之和,而误差越小,说明降维后的数据越能完整表示降维前的数据。如果这个误差小于0.01,说明降维后的数据能保留99%的信息。实际应用中,我们一般根据上式,选择能使误差小于0.01(99%的信息都被保留)或0.05(95%的信息都被保留)的最小k值。
而在实际编码,在PCA的实现过程中,对协方差矩阵做奇异值分解时,能得到S矩阵(特征值矩阵)。
PCA误差的表达式等效于下式
从代码示例中,可以看出,将数据从三维降到二维,保留了99.997%的信息。
[U,S,V] = svd(sigma) % 奇异值分解
(S[0]+S[1])/(S[0]+S[1]+S[2])
result = 0.99996991682077252
PCA的错误应用
1、将PCA用于减少过拟合。原因在于PCA只是近似地丢掉一些特征。它并不考虑任何与结果变量有关的信息,因此可能会丢失非常重要的一些特征,它并不考虑任何与结果变量有关的信息,因此可能会丢失非常重要的特征。
2、默认地将PCA作为学习过程的一部分,这虽然很多时候有效果,但最好还是从所有原始特征开始,只在有必要的时候(算法运行太慢或者占用太多内存)才考虑PCA。